Тема урока «Площадь параллелограмма», 8 класс

Цели урока:

Учебные:

вывести формулу для вычисления площади параллелограмма и показать применение этой формулы в процессе решения задач;

совершенствовать навыки решения задач.

Развивающие:

развитие у учащихся самостоятельности, инициативы и творчества, способности к самоорганизации, точности и ясности речи;

формирование навыка исследовательской деятельности;

повышение уровня математической культуры учащихся.

Воспитательные:

воспитывать аккуратность, самостоятельность, интерес к предмету.

Ход урока

1. Организационный момент.

2. Работа по готовым чертежам.

Задания:

1. Назовите известные вам формулы площадей фигур.

2. Назовите формулу площади прямоугольника.

3. Назовите формулу площади квадрата.

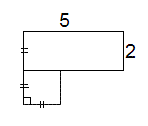
4. Найдите площадь дачного участка такой формы.

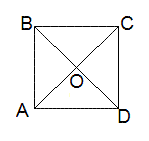
5. Участок огорода АВОСD занят картофелем. Его площадь равна 48. Найти площадь всего огорода.

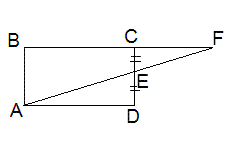
6. Площадь участка АВСД равна 50. Часть его не приносит урожай из-за неплодородной земли. Хозяин решил изменить форму своего участка. Получился  участок АВF. Какова площадь нового участка.

7. Найти площадь фигуры.

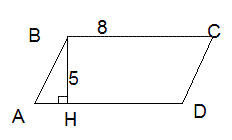
С какой проблемой вы встретились при решении этой задачи?
 Как найти площадь параллелограмма?

Совместно формулируется тема урока, ставятся цели урока,  мотивация.

3. Практическая работа.

У учеников модели параллелограммов и ножницы.

Задание:

С помощью ножниц и модели параллелограмма сделать фигуру, площадь которой умеете находить.

Ответьте на вопрос: как найти площадь параллелограмма?

Закрасьте длину и ширину прямоугольника.

Сложите обратно параллелограмм и ответьте на вопрос: изменится ли площадь фигуры?

Чем для параллелограмма являются закрашенные стороны?

Самостоятельно детьми формулируется теорема.

4. Доказательство теоремы.

Возвращаемся к задаче №7, которую мы не смогли дорешать.  Зная основание и высоту параллелограмма найти его площадь.

5. Решение задач.

1.Найдите площадь параллелограмма, если основание равно 15 см, а высота - 12 см.

2.Площадь параллелограмма 162 см, а высота 8,5 см. найдите основание.

3.Сторона параллелограмма равна 8,1см, а его диагональ, равная 14 см, образует с ней угол в 30°. Найдите  площадь параллелограмма.

6. Домашнее задание.

П.51,№459(б),461,462.

7. Подведение итогов урока.