МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 67

С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ОТДЕЛЬНЫХ ПРЕДМЕТОВ

ГОРОДА ЕКАТЕРИНБУРГА СВЕРДЛОВСКОЙ ОБЛАСТИ

Куб и конструкции из кубиков

Наглядная геометрия (5 класс)

Подготовила:

Четырина Любовь Михайловна,

учитель математики,

высшая квалификационная категория

г.Екатеринбург, 2013

Цель урока: научить распознавать на чертежах, рисунках, моделях пространственные геометрические фигуры; развивать пространственное мышление школьника; воспитать аккуратность.

Оборудование: 1. Модель куба

2. Каркасная модель куба.

3. Набор цветных кубиков.

Ход урока

Учитель: Сегодня мы с вами на уроке будем конструировать модели из пространственных геометрических фигур. Обратите внимание на стол. Какие геометрические тела вы видите?

Ученики: куб, набор кубиков.

Задания для учащихся (работа с каркасной моделью)

Учитель:

1. Покажите вершины куба, посчитайте сколько их.

2. Покажите ребра куба, посчитайте сколько их.

3. Покажите ребра, выходящие из одной вершины. Сколько их?

А теперь обратите внимание на модель куба.

4. Какая геометрическая фигура является гранью куба?

5. Сколько граней у куба?

На модели куба покажите грани, которые имеют общие ребра. Молодцы. А теперь мы научимся изображать куб схематически.

В тетради запишите число, слова "Классная работа", тему урока перепишите с доски.

(Учитель демонстрирует алгоритм построения куба на доске.) Карандашом изобразите квадрат, из его вершин в одном направлении и под одним углом проведем равные отрезки. Концы отрезков соединим между собой. А теперь отрезки, которые обозначают невидимые ребра, ластиком превратим в пунктирные линии. Куб готов.

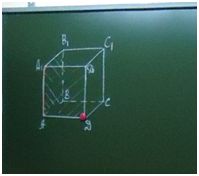
Обозначьте вершины нижнего основания заглавными буквами латинского алфавита A, B, C, D.

Вершины нижнего основания обозначим A₁, B₁, C₁, D_1. Причем вершины А и А₁ являются вершинами одного отрезка.

Задание для закрепления материала.

1. Посмотрите, какие рёбра выходят из вершины B1. Результат запишите в тетрадь (ответ В₁А₁, В₁С₁, В₁В).

2. Назовите грани, не имеющие общих вершин. Результат запишите в тетрадь (возможный вариант ABCD, A₁B₁C₁D₁).

3. Запишите в тетради рёбра, принадлежащие грани DD₁С₁С (ответ DC, D₁D, D₁C₁, C₁C).

4. Сколько рёбер не принадлежит этой же грани. Ответ запишите в тетрадь (ответ АВ, AD, BC, AA₁, BB₁, A₁D₁, A₁B₁, B₁C₁).

5. Какие отрезки лежат в гране ABCD и имеют концами вершины куба? Результат запишите в тетрадь. (Ответ АВ, ВС, CD, AD, AC, BD).

6. Запишите в тетради три вершины, не принадлежащие грани AA₁D₁D (возможный ответ В, С, С₁).

7. Соедините точки С и D₁. В какой грани лежит отрезок СD₁. Результат запишите в тетрадь (вариант ответа DD₁C₁C).

Хорошо, молодцы. А теперь мы с вами будем делать различные конструкции из кубиков, изображать их в трех видах. Учитель делает конструкцию из кубиков на подставке, чтобы результат был виден всем учащимся. Учащиеся на рабочих местах собирают такую же конструкцию из кубиков и изображают ее в трех видах в тетрадях: вид спереди, вид сверху и вид слева.

Самостоятельно решают задания № 8 и № 9 на странице 38 учебника В.А.Панчищиной "Наглядная геометрия" (М.: Просвещение, 2012 г.).

Проверка выполнения самостоятельно выполненного задания.

Домашнее задание: стр. 39, № 10, 11, 12.

Рефлексия

Оставьте на краю парты желтый кубик, если вы усвоили материал урока, и красный кубик, если не со всеми заданиями вам удалось справиться. Остальные кубики уберите в коробку.

Спасибо, положите и этот кубик в коробку. Урок окончен.

СПИСОК ЛИТЕРАТУРЫ:

1. Математика. Наглядная геометрия. 5-6 классы: учебное пособие для учащихся образовательных учреждений. [В.А.Панчищина, Э.Г.Гельфман, В.Н.Ксенева и др.] 3-е изд. – М.: Просвещение, 2012. – 175 с.

2. Примерная основная образовательная программа образовательного учреждения. Основная школа. [Сост. Е.С.Савинов.] – М.: Просвещение, 2011. – 342 с. [Стандарт второго поколения.]

3. Попова Л.П. В помощь школьному учителю: Учебно-методическое пособие. – М.: Мнемозина, 2011.

4. Поурочные разработки по математике к учебному комплекту Н.Я.Виленкина. – М.: Мнемозина, 2011.

Фото из архива автора (фотограф О.Черкасская).