Воробьева Ирина Юрьевна

учитель математики

1 категории

ГУ «Экономический лицей»

г. Семей

Методическая разработка урока

по математике

Тема урока: «Преобразование графиков тригонометрических функций»

Класс: десятый

2011год

_{Пояснительная записка}

Одной из целей современного образования является информатизация образовательного процесса. Без использования современных средств информационных технологий уже невозможно представить образовательный процесс, отвечающий требованиям современного информационного общества. Информационно–коммуникационные технологии (ИКТ) - важнейшая составляющая всех направлений деятельности современного учителя, способствующая оптимизации учебного процесса.

Проведение уроков с использованием информационных технологий – это мощный стимул в обучении. Посредством таких уроков активизируются психические и интеллектуальные процессы учащихся, стимулируется развитие познавательного интереса.

Из этого следует актуальность данной разработки урока на тему “Преобразование графиков тригонометрических функций”, которая может быть использована учителями для проведения уроков и факультативов, а так же для организации самостоятельной работы учащихся.

С помощью программы PowerPoint создана не только презентация-сопровождение для урока математики, но и интерактивная модель для демонстрации движения графика. Применение интерактивных моделей и динамических презентаций является одним из наиболее эффективных способов внедрения новых информационных технологий в преподавание математики. В этом и заключается перспективность данной разработки.

Уроки № 17-18

Тема: Преобразование графиков тригонометрических функций

Класс: 10

Целевая установка урока: научить применять преобразования графиков при построении графиков тригонометрических функций.

Ожидаемые результаты урока:

Образовательная область

Развивающая область

Воспитательная область

Систематизация знаний и умений учащихся по теме: «Преобразование графиков функций вида:

y = f(x) + m, y = f(x + t), y = аf(x), y = f(кx )», Приобретение новых навыков построения и чтения графиков тригонометрических функций , ознакомление с гармонической функцией .

Развитие умения работать с имеющейся информацией в необычной ситуации; развитие логического мышления, памяти и других значимых качеств личности учащихся; развитие самостоятельной творческой исследовательской деятельности, развитие способности к самооценки .

.

Воспитание графической культуры, умения видеть красоту математики, уважительного отношения друг к другу. Повышение интереса к предмету.

Тип урока: формирование новых знаний

Межпредметные связи: информатика, физика.

Формы, методы, приёмы работы: фронтальная беседа, работа учащихся в группах, индивидуальная работа.

Ресурсы: интерактивное оборудование, презентация на интерактивной доске, раздаточный материал: карточки-задания для групп, цветные карандаши, шаблоны графика y = sinx.

Ход урока:

Этапы урока

Содержание деятельности учителя

Содержание деятельности учащихся

1.Орг. момент

(3 мин.)

Приветствует учащихся, проверяет готовность к уроку. Сообщает тему и цель урока. Приложение 1

Учитель сам назначает лидеров и просит их создать 4 группы. Каждой группе дается лист достижений Приложение 2

Приветствуют учителя, настраиваются на работу. Записывают тему урока в тетрадь.

Класс делится на 4 группы, которые объединяются около лидеров.

2.Актуализация знаний учащихся

(10 мин.)

Фронтальная беседа с классом: учитель задает вопросы, обращаясь поочереди к каждой группе

«Как называется преобразование? Что происходит с функцией? Как преобразование зависит от коэффициента?»

Приложение 3.(слайды презентации раскрываются постепенно шаг за шагом)

Затем на экране появляются два слайда, которые в виде интерактивной картинки напоминают свойства функций синуса и косинуса.

Отвечают и успешные ответы отмечают в листе достижений 1 баллом

Один ученик комментирует свойства

3. Изучение нового

(25 мин.)

Каждой группе даются карточки с заданиями определенного типа преобразований. Приложение4

Учитель ставит проблемный вопрос: «Меняя параметры, определи, как называется преобразование функции и отметь те свойства функций, которые изменяются при этом преобразовании». (15 мин.)

Оценивает правильность ответов каждой группы и подводит итог этой работы. (5 мин.)

С помощью презентации демонстрируются преобразования тригонометрических функций Приложение 5 (5 мин.)

Сами распределяют задания между собой, так, чтобы можно было решить все, выполняют чертежи с помощью шаблонов в тетрадях.

В заключении учащиеся делают соответствующие выводы и готовятся к устному выступлению. Результаты работы других групп записывают в тетрадь.

4.Закрепление

(20 мин.)

Каждой группе дает две карточки с одинаковыми заданиями:

«По свойствам функции определите, какое преобразование было совершено над функцией и задайте функцию формулой».

Проверьте самостоятельную работу с помощью интерактивной доски . Приложение 6

Выполняют задание в тетради и делают соответствующие выводы в карточках, из которых одну отдают учителю. Проверяют работу, выставляют баллы в листе достижений.

5.Изучение нового

( 10 мин.)

Дает определение гармонической функции и показывает алгоритм построения на слайдах. Приложение 7

(10 мин.)

Записывают в тетрадях.

6.Закрепление

(12мин.)

Опишите алгоритм построения для следующей функции: у =2 Можно ли ее назвать гармонической? Найдите, чему равна амплитуда, фаза и частота колебания . (7 мин.) После этого задает загадку: «Что общего между качелями, музыкой и светом?». Ответ демонстрируется с помощью слайда. Приложение 8 (5 мин)

Записывают в тетрадях, один из учащихся комментирует ответ.

Учащиеся вступают в дискуссию

7.Домашнее задание

(3 мин).

Постройте график функции:

,, .,

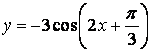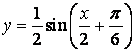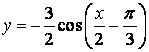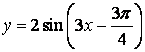Записывают в тетрадях

8.Рефлексия

(3 мин.)

Задайте формулой любую гармоническую функцию и запишите на листочке одним из следующих  цветов, которые на ваш взгляд соответствуют вашему настроению от проделанной вами работы
Красный - отличное
Зеленый - хорошее
Синий - удовлетворительное

9. Итог урока

(4 мин.)

Мы повторили правила преобразований графиков функций вида: y = f(x) + m, y = f(x + t), y = аf(x), y = f(кx )», Построили преобразования тригонометрических функций и описали свойства. Познакомились с гармонической функцией.

Заполняют листы достижений и подводят итоги урока в баллах.

Дополнительная информация к уроку

Приложение 1: Лист достижений группы

Приложение 2: Слайды по теме «Задачи урока»

Приложение 3: Слайды по теме «Преобразование графиков функций»

Приложение 4: Карточки для группы на первый этап работы.

Приложение 5: Слайды по теме «Преобразование тригонометрических

функций»

Приложение 6: Карточка для группы для второго этапа урока

Приложение 7: Слайды по теме «Гармоническая функция»

Приложение 8: Слайды по теме «Загадка урока»

Приложение 9: Домашнее задание

Приложение 1 Лист достижений группы

Лист достижений группы № ______

Лидер группы ____________________________________________

Учащиеся группы_________________________________________

_________________________________________

_________________________________________

_________________________________________

_________________________________________

Количество набранных баллов группы

Повторение(1 балл за ответ)________________________________

I этап работы в группе

Количество набранных баллов_____________________________

II этап работы в группе (задание: по свойствам определить функцию)

Количество набранных баллов______________________________

Итоговый балл группы_____________________________________

Приложение 4 Карточки для группы на первый этап работы.

Группа 1

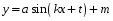: a=1, k=1, m=0, t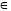{1, 2, 3, -1, -2}

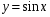и

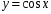
Меняя параметр t, определи какое преобразование функции и впиши свойства

Основные функции

Сдвиг вдоль оси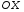

Сдвиг вдоль оси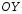

Сжатие вдоль

оси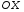

Сжатие вдоль

оси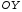

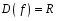
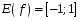
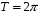
Вывод (какие преобразования меняют свойства основных функций):________________________________________________

Баллы (5 б)______________________________________________

Примените эти преобразования к функции y= tg ( x+ 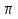\2)___________

Баллы (2б)______________________________________________

Итого

Группа №1

Группа №2

Группа №3

Группа №4

Группа 2

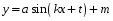: t=0, k=1, m=0, a 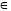{1, 2, 3, 1/2, 1/3 }

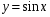и

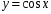
Меняя параметр a, определи какое преобразование функции и впиши свойства

Основная функция

Сдвиг по оси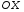

Сдвиг по оси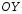

Сжатие по

оси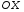

Сжатие по

оси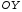

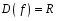
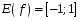
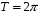
Вывод (какие преобразования меняют свойства основных функций):_____________________________________________________

Баллы (5 б)______________________________________________

Примените эти преобразования к функции y= 2tg x ___________

Баллы (2 б)______________________________________________

Итого

Группа №1

Группа №2

Группа №3

Группа №4

Группа 3

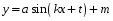: t=0, a=1, m=0, k 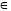{1, 2, 3, , 1/2, 1/3, }

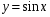и

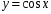
Меняя параметр k, определи какое преобразование функции и впиши свойства

Основная функция

Сдвиг по оси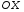

Сдвиг по оси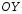

Сжатие по

оси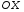

Сжатие по

оси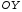

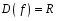
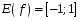
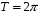
Вывод (какие преобразования меняют свойства основных функций):_____________________________________________________

Баллы (5 б)______________________________________________

Примените эти преобразования к функции y= ctg 2x _____________________________________________________________

______________________________________________________________

Баллы (2 б)______________________________________________

Итого

Группа №1

Группа №2

Группа №3

Группа №4

Группа 4

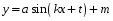: t=0, a=1, k=1, m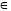{1, 2, 3, -1, -2, }

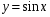и

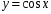
Меняя параметр m, определи какое преобразование функции и впиши свойства

Основная функция

Сдвиг по оси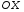

Сдвиг по оси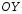

Сжатие по

оси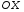

Сжатие по

оси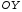

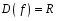
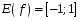
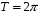
Вывод (какие преобразования меняют свойства основных функций):_____________________________________________________

______________________________________________________________

Баллы (5 б)______________________________________________

Примените эти преобразования к функции y= ctg x + 4 ____________________________________________________________

______________________________________________________________

Баллы (2 б)______________________________________________

Итого

Группа №1

Группа №2

Группа №3

Группа №4

Приложение 6 Карточка группы для второго этапа урока

Группа № ________

Задание: По свойствам функции определите, какое преобразование было совершено над функцией и задайте функцию формулой.

1. (1 балл) 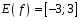и ___________________________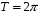

__________________________________________________________

2. (1 балл) 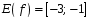и _________________________

__________________________________________________________

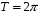3. (2 балла) 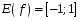, 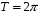и ______________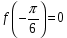

__________________________________________________________

4. (1 балл) 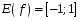и ____________________________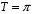

__________________________________________________________

5. (1 балл) 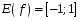и ___________________________

__________________________________________________________

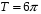6. (2 балла) 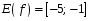и ________________________

__________________________________________________________

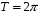7. (2 балла) 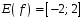и _________________________

__________________________________________________________

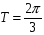8. (3 балла) 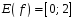, 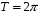и _______________

__________________________________________________________

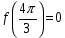9. (3 балла) 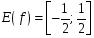, 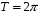и _____________

__________________________________________________________

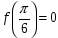10. (2 балла) 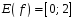и __________________________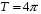

Всего баллов:

Лист ответов:

1. (1 балл) 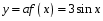Растяжение по оси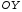

2. (1 балл) 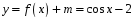Сдвиг по оси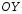

3. (2 балла) 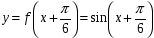Сдвиг по оси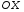

4. (1 балл) 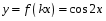Сжатие по оси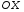

5. (1 балл) 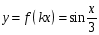Растяжение по оси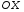

6. (2 балла) 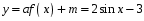Растяжение по оси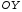

и Сдвиг по оси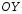

7. (2 балла) 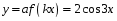Сжатие по оси 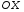и Растяжение по оси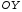

8. (3 балла) 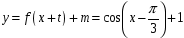Сдвиг по оси 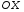и Сдвиг по оси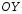

9. (3 балла) 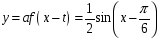Сдвиг по ос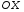и и

Сжатие по оси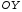

10. (2 балла) 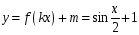Сдвиг по оси 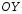и Растяжение по оси