Методические рекомендации к внеурочной самостоятельной работе: "Вычисление определителей матриц второго и третьего порядка"

Самостоятельная работа №1:

Вычисление определителей матриц второго и третьего порядка

Цель работы: овладение методами вычисления определителей второго и третьего порядков.

Студент должен:

Знать:

форму записи определителя и используемую символику
свойства определителей
Теорему Лапласа (о разложении определителя квадратной матрицы с помощью алгебраических дополнений по элементам строки или столбца)
правило Сарусса

Уметь:

вычислять определители первого, второго и третьего порядка
строить миноры и вычислять алгебраические дополнения

Форма выполнения задания: решение задач (письменно)

Время выполнения 20 минут

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1 В чем различие между матрицей и определителем?

2 В чем суть метода разложения определителя по строке или столбцу?

Формирование компетенций:.

Рекомендации по выполнению.

1.Разобрать решение примеров.

2.Выполнить задания тренажера, используя указания.

3.Оформить решение задач тренажера в тетради.

Основной теоретический материал

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно).

Определитель матрицы А обозначается как: det(A), |А| или Δ(A

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

$\Delta=\begin{vmatrix} a_{11}\end{vmatrix} = a_{11}$

Определители второго и третьего порядка.
Пусть 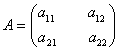- квадратная матрица 2-го порядка.

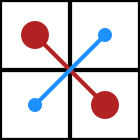140px-Determinant_2x2 Схема расчета определителя матрицы 2×2.

Определителем 2-го порядка (матрицы а) называется число
D(А) = .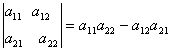

Решение типовых примеров
Пример. Вычислить определитель матрицы

.
РЕШЕНИЕ. D(А) = .

Пусть - матрица 3-го порядка.

Определителем 3-го порядка (матрицы А) называется число

D(А) =
Правило Саррюса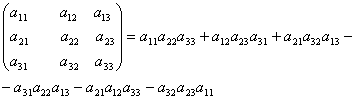(треугольника)

Схема вычисления определителя третьего порядна

pic_1

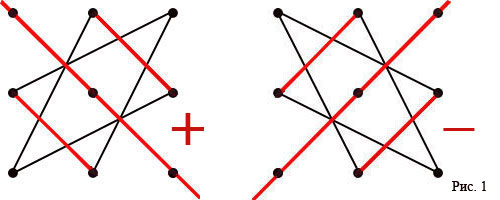
Первые два столбца матрицы записываются справа возле матрицы. Произведения элементов, стоящих на линях со знаком «плюс», складываются, затем вычитаются произведения элементов, находящихся на линях со знаком «минус»

$\det(A)= a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}$

Пример. Вычислить определить

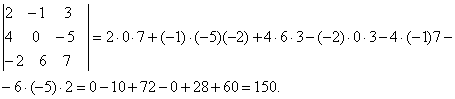
Минором элемента a_ik называется определитель М_ik, составленный из элементов, оставшихся после вычеркивания из матрицы А i-ой строки и k-го столбца.

Алгебраическим дополнением элемента a_ik называется число .
Определителем 3-го порядка (матрицы А) называется сумма произведений элементов первой строки матрицы на их алгебраические допоплнения:
D(А) =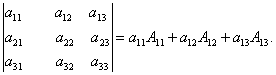
Данную формулу называют разложением определителя по первой строке.

Решение типовых примеров
Пример. Вычислить определитель матрицы третьего порядка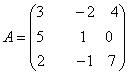
.

Решение. Находим миноры и алгебраические дополнения элементов 1-ой строки матрицы: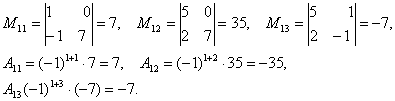

Вычисляем искомый определитель:
D(А) = 3^.7 + (-2)^.(-35) + 4^.(-7) = 63

.
Далее индуктивно вводится понятие определителей более высоких порядков.

Для матрицы $n \times n$ определитель задаётся рекурсивно:

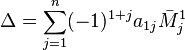$\Delta=\sum_{j=1}^n (-1)^{1+j} a_{1j}\bar M_j^1$ , где $\bar M_j^1$ — дополнительный минор к элементу $a_{1j}$ . Эта формула называется разложением по строке.

Решение типовых примеров

Пример 1

det A =

-2

= 4 * 2 * 2 + ( -2) * 12 * 1 + 4 * 10 * 2 - 4 * 2 * 1 - ( -2) * 10 * 2 - 4 * 12 * 2 = 8

Пример 2

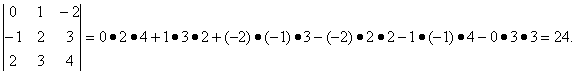
determinants_clip_image022

Самостоятельная работа

Вычислить определитель второго порядка всем

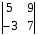
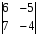
1 вариант

Вычислить определитель по первой строке

2 вариант

Вычислить определитель по первой строке

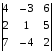
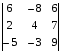
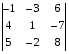
Вычислить определитель по правилу треугольника

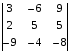
3 вариант

Вычислить определитель по третьему столбцу

4 вариант

Вычислить определитель по третьему столбцу

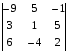
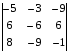
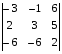
Вычислить определитель по правилу треугольника

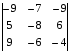
5 вариант

Вычислить определитель по правилу треугольника

6 вариант

Вычислить определитель по правилу треугольника

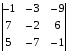
Вычислить определитель по второй строке

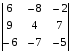
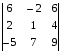
Вычислить определитель по второму столбцу

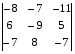
7 вариант

Вычислить определитель по второй строке

8 вариант

Вычислить определитель по второму столбцу

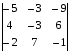
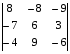
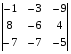
Вычислить определитель по правилу треугольника

Оформить отчет.

Требования к оформлению самостоятельной работы

Расчетные задания должны быть выполнены в рабочей тетради.

По результатам решения тренажера выставляется оценка, которая учитывается при приеме дифференцированного зачета.

Шкала оценки образовательных достижений

Процент результативности

(правильных ответов)

Оценка уровня подготовки

Балл (оценка)

Вербальный аналог

90-100

отлично

80-89

хорошо

70-79

удовлетворительно

менее 70

неудовлетворительно

Литература:

Григорьев С.Г., Задулина С.В. Под редакцией В.А. Гусева Математика. – М.: Образовательно-издательский центр «Академия», 2012
Пехлецкий И.Д. Математика. – М.: Образовательно-издательский центр «Академия», 2012.

Дополнительная литература:

Н.В. Богомолов. Практические занятия по математике. - М., ВШ,2006.
Н.В. Богомолов, П.И. Самойленко. Математика.-М., Дрофа,2008.

Интернет ресурсы:

Листать вверх Листать вниз

Получить код

Скачать материал (0.09 Мб)

Нравится материал? Поддержи автора!

Ещё документы из категории математика:

Контрольная работа по математике за 1 и 2 курс

Конспект урока по математике "Применение преобразования целого выражения" 8 класс

Конспект урока по математике "Преобразование выражений, содержащих логарифмы" 11 класс

План-конспект урока по математике "Измерение углов" 5 класс

Тест по математике "Сложение и вычитание многочленов" 7 класс

Конспект урока по математике в 6 классе "Противоположные числа. Модуль числа"

Внеклассное мероприятие по математике «Клуб веселых математиков»