Открытая олимпиада школьников

«Интеллектуальный марафон»2012-2013гг.

Математика. 9 класс.

1 часть.

Решения заданий записывать. (За каждое задание 5 баллов, всего 50 баллов).

1. Укажите, какие из перечисленных ниже утверждений верны:

1) В параллелограмме противолежащие углы равны.

2) Вокруг любого прямоугольника можно описать окружность.

3) В любом параллелограмме диагонали перпендикулярны.

4) Квадрат – это ромб, у которого все углы прямые.

5) В любой четырехугольник можно вписать окружность.

2. Упростите выражение

3. Постройте график уравнения . В ответе укажите площадь где точка О – начало координат, а точки А и В – точки пересечения данной прямой с осями координат.

4. Укажите график функции, заданной формулой

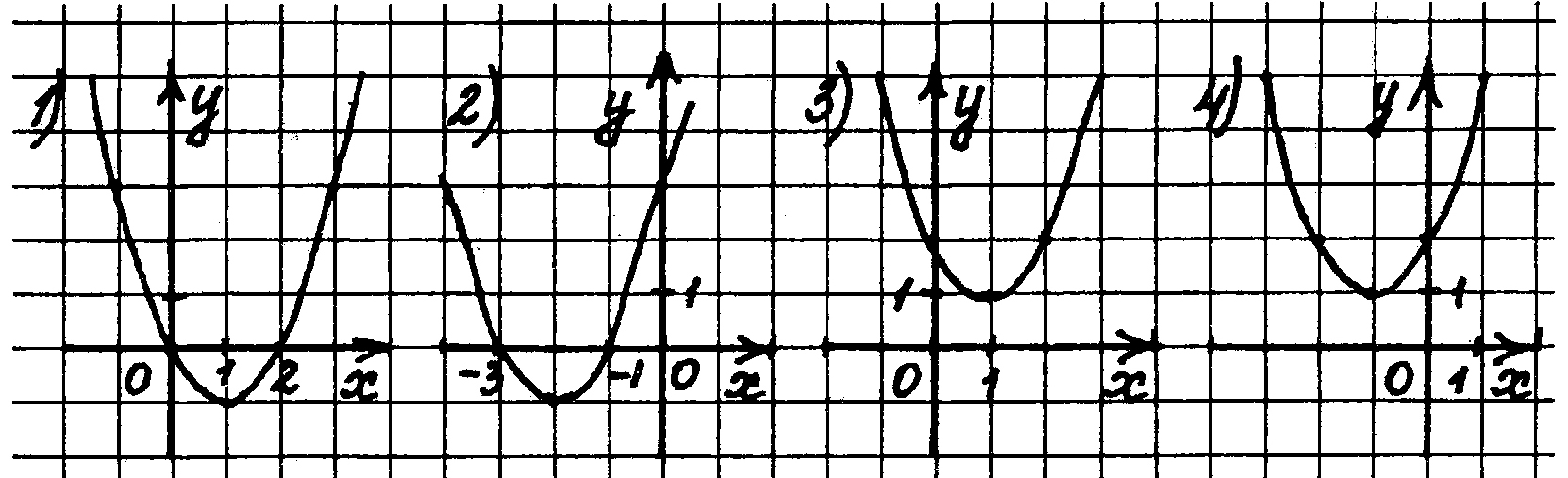
5. При каких значениях множество значений функции

6. Найдите область определения функции

7. В уравнении выразите переменную х через у.

8. Если одну сторону прямоугольника увеличить на 40%, а смежную сторону уменьшить на 30%, то как изменится площадь прямоугольника?

1) увеличится на 10%; 2) уменьшится на 10 %; 3) увеличится на 5%; 4) уменьшится на 2%.

9. По данным рисунка найдите площадь заштрихованной фи­гуры (NK, KL, LM , MN — дуги с цент­рами в вершинах А, В, C и D квадрата ABCD; взять , ответ округлить до сотых).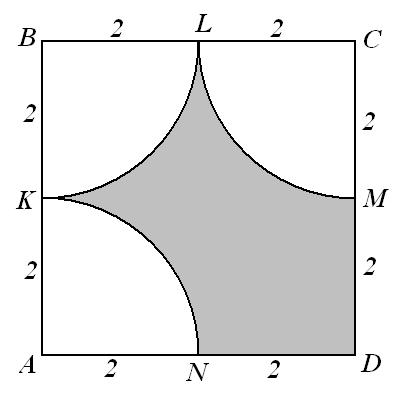

10. В прямоугольном треугольнике АВС на катете АВ как на диаметре, построена окружность, разбивающая гипотенузу на части в отношении 3:2, считая от вершины С. Найти площадь треугольника АВС, если его гипотенуза равна 10 ().

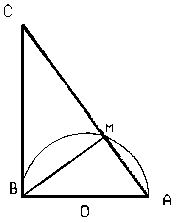
2 часть.

Задание 1. (15 баллов).

Найдите сумму корней уравнения

и укажите, при каких значениях a эта сумма принимает наибольшее значение.

Задание 2. (15 баллов).

Бассейн для плавания наполняется водой двумя кранами за 1 час 12 минут. Если второй кран закрыть через 1 час, то для наполнения бассейна первый кран должен быть открыт ещё в течение 20 минут. За какое время наполняется бассейн каждым краном в отдельности.

Задание 3. (20 баллов) Решите уравнение .

Ответы:

Часть 1.

1

2

3

4

5

6

7

8

9

10

1,2,4

8/9

2

-4; 4;

уменьшится на 2%.

6,58

24,4

Часть 2.

Задание 1. (15 баллов).

Найдите сумму корней уравнения

и укажите, при каких значениях a эта сумма принимает наибольшее значение.

Решение

Найдем значения параметра a, при которых уравнение будет иметь действительные корни. Дискриминант квадратного уравнения должен быть неотрицательным: .

Найдем значение дискриминанта:

.

. Положим , получим систему неравенств:

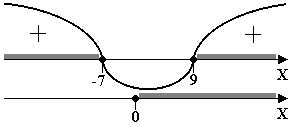
Получим, ,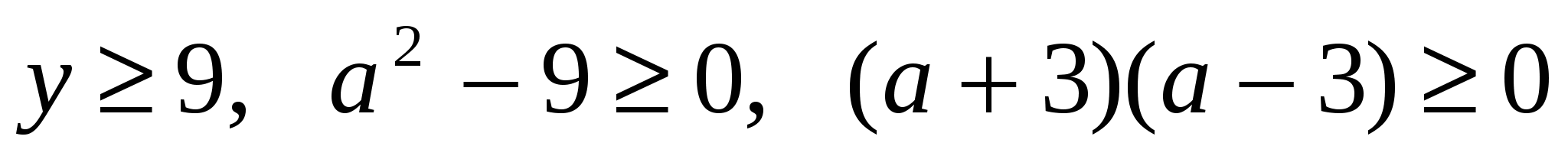

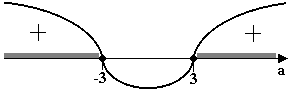
При и или 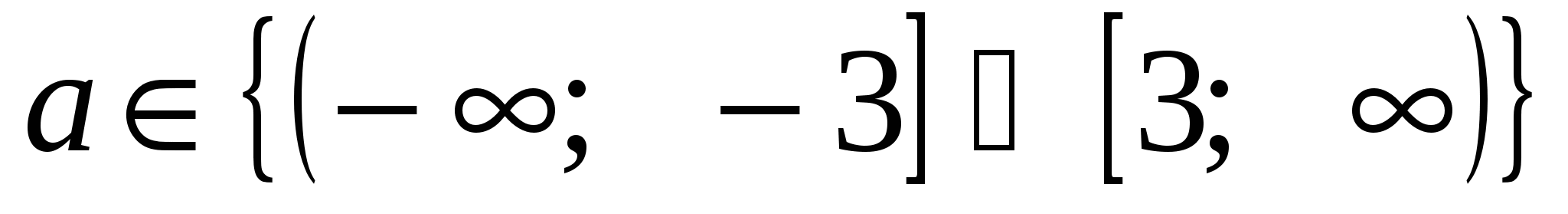уравнение имеет действительные корни. Поскольку уравнение приведенное, то, по теореме Виета, сумма корней уравнения будет равна второму коэффициенту с противоположным знаком:

.

Рассмотрим это выражение как функцию от a и найдем ее наибольшее значение на промежутках .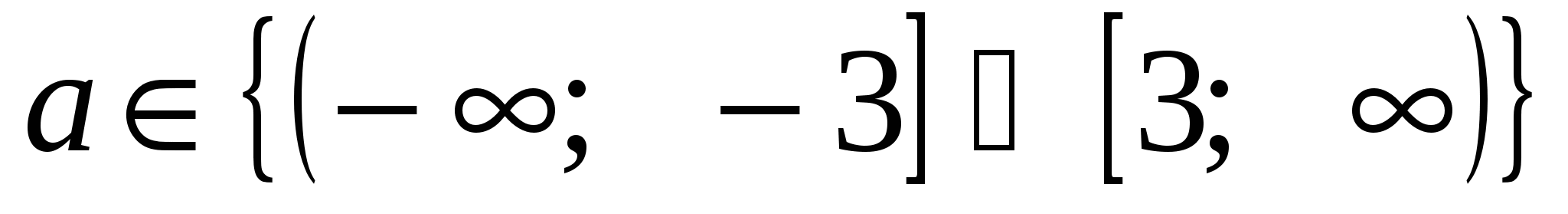

Графиком функции является парабола с вершиной в точке 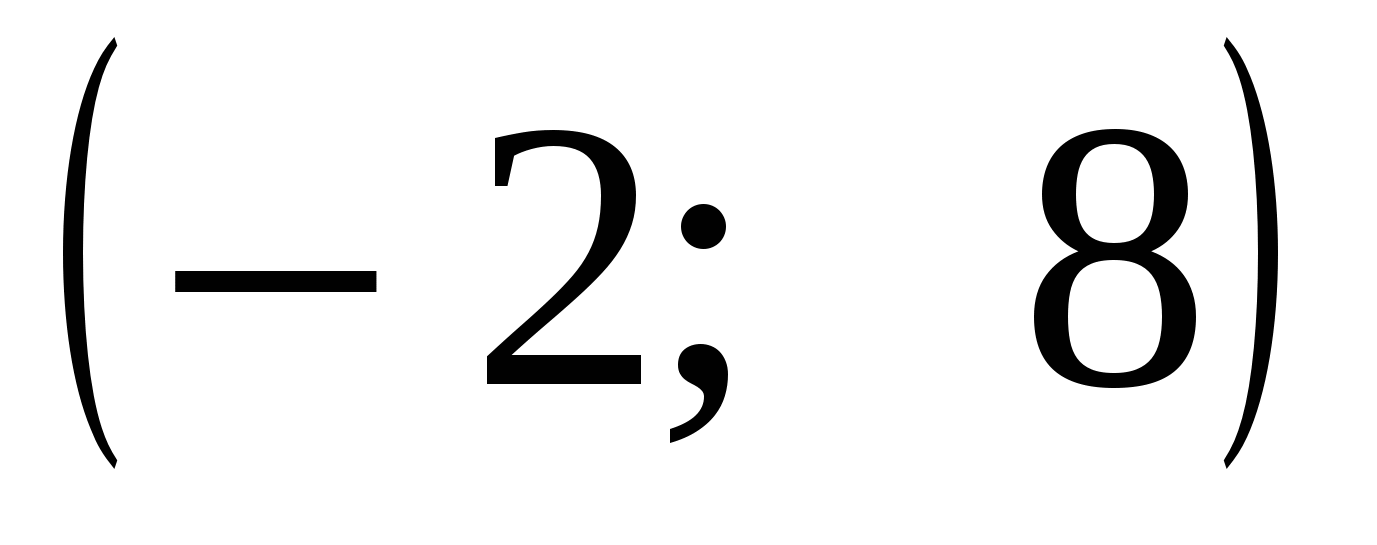, ветви которой направлены вниз. Она пересекает ось абсцисс в точках: .

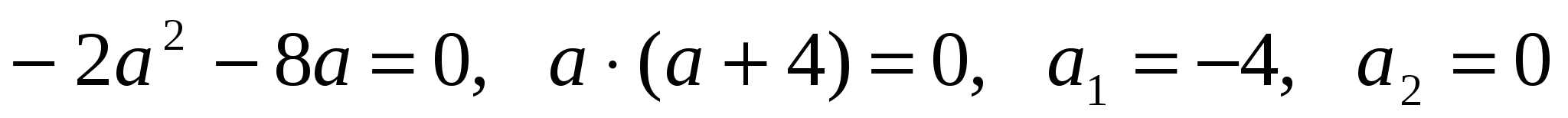Начертим схематически график этой функции на множестве и .

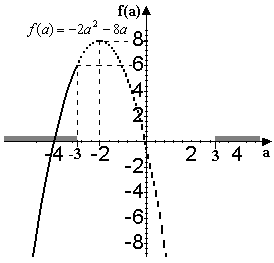
Очевидно, что наибольшее значение функция принимает в точке a = -3 и принимает значение .

Ответ: При 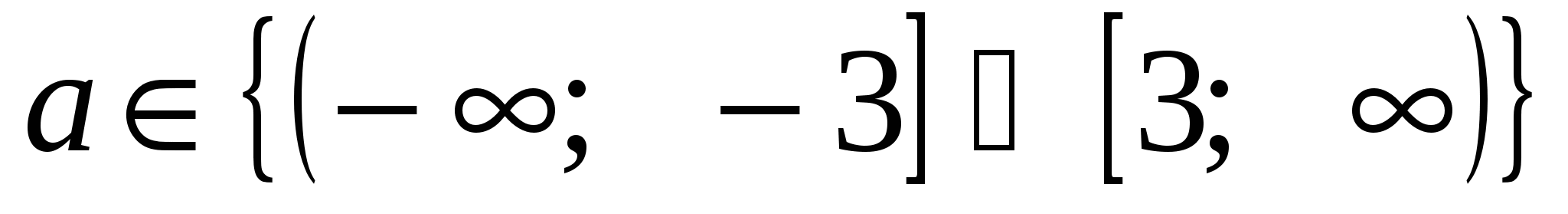сумма корней равна и принимает наибольшее значение при a = -3, равное 6.

Задание 2. (15 баллов).

Бассейн для плавания наполняется водой двумя кранами за 1 час 12 минут. Если второй кран закрыть через 1 час, то для наполнения бассейна первый кран должен быть открыт ещё в течение 20 минут. За какое время наполняется бассейн каждым краном в отдельности.

Решение

Пусть x час - время, за которое наполняется весь бассейн первым краном, если он открыт только один;

y час - время, за которое наполняется весь бассейн вторым краном, если он открыт только один;

1 - вся работа, т. е. наполнение всего бассейна водой;

- делает работы за 1 час первый кран, производительность первого крана;

- делает работы за 1 час второй кран, производительность второго крана;

- делают за 1 час два крана, будучи открыты вместе, совместная производительность двух кранов.

По условию, двумя кранами бассейн наполняется водой за 1 час 12 мин, т. е. за часа, значит, .

Если второй кран закрыть через 1 час, тогда вместе два крана за это время выполнят работы .

Первый кран, при этом должен еще работать 20 минут, т. е. 1/3 часа.

За это время он выполнит работу .

По условию, тогда вместе они выполнят всю работу:

.

Получим систему уравнений:

.

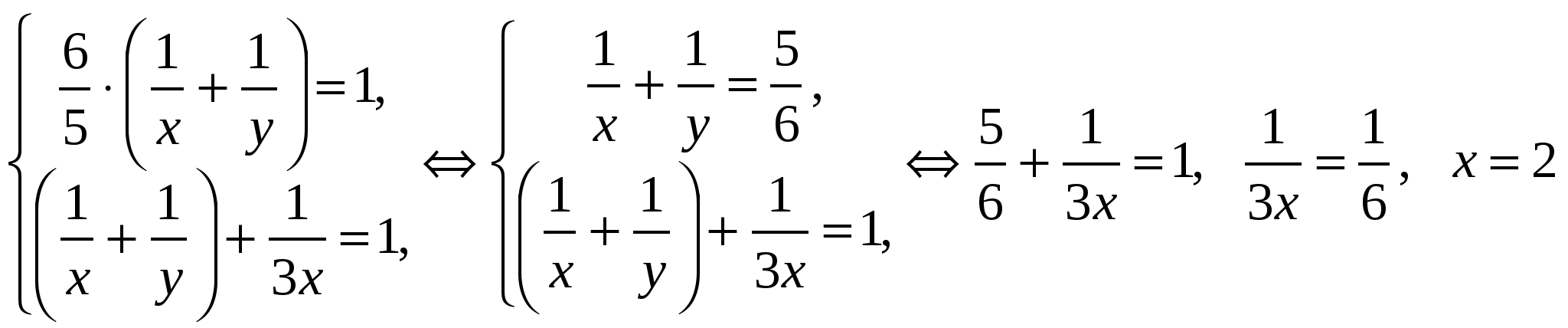Подставляя это значение в первое уравнение системы, находим y:

.

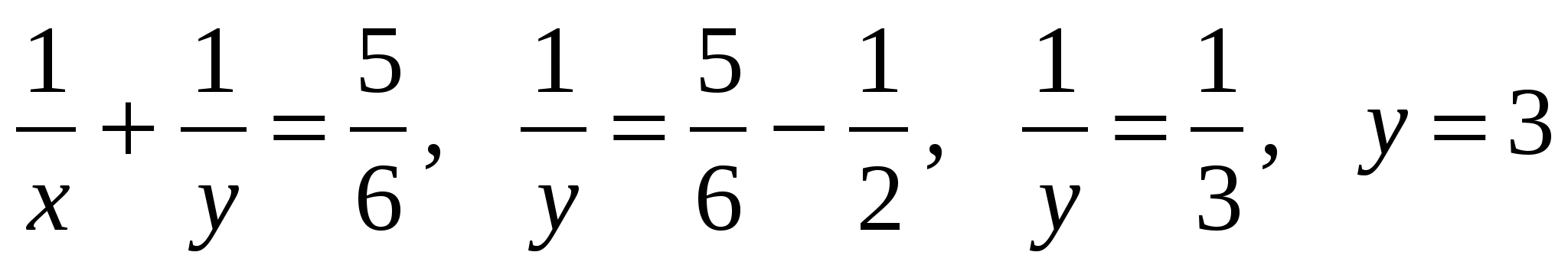Ответ: за 2 часа первый кран наполнит бассейн, работая один;

за 3 часа второй кран наполнит бассейн, работая один.

Задание 3. (20 баллов)

Решите уравнение .

Решение. Один из возможных способов решения данного уравнения является введение параметра. Пусть , тогда уравнение примет вид:

.

Заметим, что оно является квадратным относительно а. Перепишем его в виде: .

Его дискриминант равен .

Тогда ; .

Значит исходное уравнение равносильно совокупности двух уравнений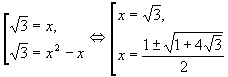

Ответ: .

Критерии оценивания.

Каждая работа оценивается и проверяется, не менее чем 2-мя членами жюри.

1 часть (по 5 баллов).

5 баллов ставится за верное решение;

4 балла – за верное решение с недочетом;

2-3 балла – решение в основных чертах верное, но неполное или содержит непринципиальные ошибки;

1 балл – решение в целом неверное, но содержит более или менее существенное продвижение в верном направлении;

0 баллов – решение неверное или отсутствует.

2 часть.

1 задание.

15 баллов – решение верное, даны необходимые пояснения;

10 баллов – в решении допущена техническая ошибка и решение доведено до конца;

5 баллов – идея решения верная, недостаточны пояснения или допущена техническая ошибка, и решение не доведено до конца;

0 баллов – решение неверное или отсутствует.

2 задание.

15 баллов – решение верное и приведены необходимые пояснения;

10 баллов – решение верное, но нет необходимых пояснений;

5 баллов – идея решения верная, решение доведено до конца, но есть ошибка в решении системы уравнений, влияющая на ответ или при верном решении оно не доведено до конца;

0 баллов – решение неверное или отсутствует совсем.

3 задание.

20 баллов – решение верное и приведены необходимые пояснения;

15 баллов – идея решения верная, решение доведено до конца, но допущена техническая ошибка при записи корней;

10 баллов – идея решения верная, но решение не доведено до конца (не найдены корни);

5 баллов – идея решения верная, но допущена ошибка в составлении дискриминанта или определении его знака и решение не доведено до конца;

0 баллов – решение неверное или отсутствует совсем.