Предметная неделя по математике

Цель: создание условий для развития интереса учащихся к математике.

Задачи:

1. Активизация познавательной деятельности обучающихся.

2. Развитие интеллектуальных и творческих способностей, остроты мышления и наблюдательности.

3. Воспитание самостоятельности, чувства ответственности, культуры коллективного общения.

- Ребята, у нас начинается математическая неделя. Сегодня вы познакомитесь с загадочным и интересным миром  математики. Увидите, как разнообразен и увлекателен этот мир. Математика – одна из важнейших наук.

- В путешествие по этой стране мы берем с собой самых смелых, дружных, сообразительных и находчивых математиков. В пути вам потребуются: смекалка, сообразительность, внимание.- А есть ли среди вас такие?

В глубину веков... В древние времена не существовало единой для всех стран системы счета.
Еще каких-то пятьсот лет назад единого счёта не было даже в просвещенной Европе, не говоря уже о какой-нибудь Африке или Америке. Но, тем не менее, люди все равно числа как-то записывали. У каждого народа была своя собственная или позаимствованная у соседа система записи чисел. Одни использовали буковки, другие - значки, третьи - закорючки. У кого-то получалось удобнее, у кого-то не очень. Позднее человек научился использовать символы для разных единиц счета. Он рисовал черточку или другую отметку для любого предмета, который он считал, но у него по-прежнему не было слов, чтобы обозначить цифры. Еще позднее человек начал считать с помощью пальцев на руке.
Система счета, которую мы используем сегодня, была изобретена в Индии тысячу лет назад. Арабские купцы распространили ее по всей Европе к 900 году. В этой системе использовались цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 и 0. Это десятичная система, построенная на основе десятки. Так как у нас 10 пальцев на руках, это привело к использованию цифры 10 в системах счета. Славянская кириллическая десятеричная алфавитная нумерация. Слайд 3 Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию. Древнекитайская система счисления. Слайд 4 Эта система одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае. Система счисления индейцев Майя. Слайд 5 Эта система очень интересна тем, что на ее развитие не повлияла ни одна из цивилизаций Европы и Азии. Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Основанием этой системы было число 20, хотя сильно заметны следы пятеричной системы. Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять). Римская система счисления. Слайд 6 Это самая известная система, после «арабской», она возникла более двух с половиной тысяч лет назад в Древнем Риме. Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Римскими цифрами  пользовались  очень долго.  Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами  (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д. Новая или арабская нумерация. Слайд 7 Система счета, которую мы используем сегодня, была изобретена в Индии тысячу лет назад. Это, самая распространенная на сегодняшний день нумерация. Название "арабская" для нее не совсем верно, поскольку хоть и завезли ее в Европу из арабских стран, но там она тоже была не родной. Арабские купцы распространили ее по всей Европе к 900 году. В этой системе использовались цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 и 0. Это десятичная система, построенная на основе десятки. Так как у нас 10 пальцев на руках, это привело к использованию цифры 10 в системах счета. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке

Ведущий.

- И так, готовы? В путь!

1 «Математическая лотерея»

Игра состоит в решение простых шуточных задач, простейших ребусов.

Примеры заданий:

1) Предлог стоит в моём начале,

В конце же - загородный дом.

А целое мы все решали

И у доски, и за столом. (За + дача = задача)

2) Он грызун не очень мелкий,

Ибо чуть побольше белки.

А заменишь «У» на «О» -

Будет круглое число. (Сурок - сорок)

3) С «К» - фигура без углов,

С «Д» - дружить с тобой готов. (Круг - друг)

Число богатырей в «Сказке о мертвой царевне»

7

Число богатырей, братьев царевны – Лебедь

33

Число разбойников, врагов Али – Бабы

40

2. «Магический квадрат». слайд 8

В пустые клетки расставить числа 3, 4, 5, 6, 8, 9 так, чтобы по горизонтали, вертикали и диагонали сумма была равна 21. Какая команда быстрее выполнит это задание, та и побеждает в этом конкурсе.

10

3

8

5

7

9

6

11

4

3.Найди закономерность слайд 9

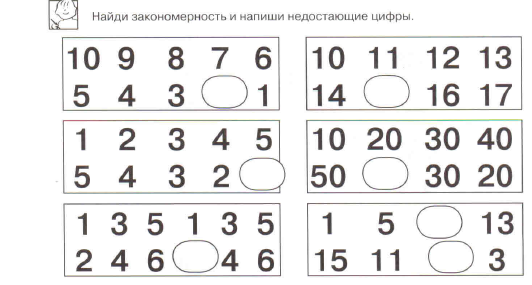
4.Поставь знаки Слайд10

Слайд11.

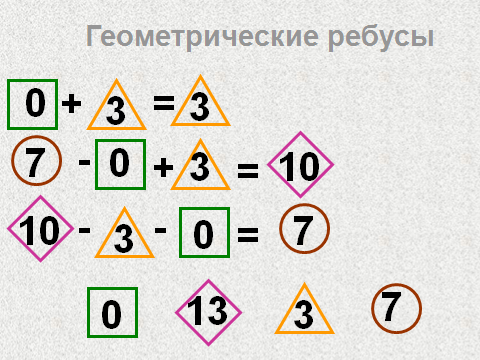
5. Конкурс капитанов. (слайд 12)

На табло числа от 1 до 32. Капитаны должны их называть в порядке возрастания и показывать в течение 2 минут. Кто больше назовет чисел, тот и побеждает.

9

7

11

17

15

20

24

4

8

2

26

5

28

21

12

23

32

25

19

18

27

6

1

22

3

30

29

14

10

16

31

13

6. «Лучший конструктор».

Из цветной бумаги вырезать геометрические фигуры и из них сделать аппликацию. У какой команды на картине больше окажется геометрических фигур, та получает 5 баллов, а другая на усмотрение жюри.

7.Математический марафон

Сложение и вычитание в пределах 100

1. К 3 десяткам прибавить 7 единиц.

2. Из 47 вычесть 40.

3. Уменьшаемое 80, вычитаемое 30, найти разность.

4. Сколько вычесть из 17, чтобы получилось 8?

5. Сколько прибавить к 7, чтобы получилось 18?

6. Уменьшаемое 24, вычитаемое 5, назовите разность.

7. Из скольки вычесть 11, чтобы получилось 21?

8. 48 единиц уменьшить на 2 десятка.

9. К 3 десяткам прибавить 4 десятка.

Геометрические фигуры

1. Как называется линия, имеющая начало, но не имеющая конца?(луч)

2. Как называется фигура, не имеющая углов?(круг)

3. Дайте иное определение ломаной замкнутой линии из 3 звеньев.(треугольник)

4. Как называется прямоугольник с 4 равными сторонами?(квадрат)

5. Что находится сложением всех длин сторон многоугольника?(периметр)

Компоненты действий

1. Как называется первый компонент при сложении?(слагаемое)

2. Что найдём, если к вычитаемому прибавим разность?(уменьшаемое)

3. Как называется второй компонент при вычитании?(вычитаемое)

Подведение итогов.