Творческая мастерская учителя

Запомнить так,

чтоб не забыть

Автор-составитель: Е.В. Глебова, учитель математики МОУ «Гимназия», г. Великий Устюг

Рецензенты: Кульневский М.Г., Сверкунов К.Г.

Запомнить так, чтобы не забыть, 5-9 классы: приёмы запоминания и ассоциации в математике (авт.- сост. Е.В. Глебова - Великий Устюг: « Малая академия», 2013.- 44с.

Изучение математики детьми с гуманитарным складом ума требует особого труда, использования нестандартных приёмов запоминания.

Вниманию читателя предложены разнообразные ассоциации на математические понятия; способы запоминания терминов.

Пособие предназначено учащимся и учителям школ, гимназий; рассчитано на творческое использование.

2013

Введение

Бывает, что во время

урока математики, когда даже воздух стынет от скуки,

в класс со двора влетает бабочка…

А.П. Чехов

Математику должны изучать все дети; дети с разными

способностями, склонностями, предпочтениями…

Как заинтересовать гуманитарно-ориентированных детей непростым школьным предметом, как математика? Как помочь увидеть изящество и красоту её стройных формул? Возможно, пособие, которое вы держите в руках, поможет найти ответы на эти вопросы. А так же поможет запомнить всё изучаемое так, чтобы не забыть.

Данное пособие можно использовать как в математических классах, так и гуманитарных. Мы приводим нетрадиционные формы запоминания, литературные минутки, исторические экскурсы, привлекаем большое количество ассоциаций и пр.

Мы предприняли попытку систематизировать материал по математике 5-9 классов, упорядочить по темам.

Пособие представляет своеобразный дидактический материал, возможности применения которого могут варьировать по усмотрению учителя.

I раздел пособия посвящён ассоциациям и аналогиям между математическими и литературными объектами.

Во II разделе рассмотрены темы алгебра и геометрия 5-9 классов с приёмами запоминания.

В III разделе рассмотрены темы геометрии 5-9 классов с технологиями запоминания.

Предложенные материалы сопровождаются теоретическими положениями, обосновывающими актуальность использования предлагаемого материала, комментариями автора.

Пособие будет полезно и при внеклассных занятиях по предмету, проведении конкурсов, викторин.

Работая над пособием, мы ставили пред собой цель- помочь ученикам запомнить «сухие» математические факты, создать для гуманитариев более комфортную атмосферу на уроке, облегчить процесс приобретения и сохранения знаний.

К. Бальмонт дал напутствие своему читателю: « Умей творить из самых малых крох, иначе для чего же ты кудесник?»

Хочется надеяться, что мой опыт и идеи, собранные по крупицам и систематизированные в данном пособии, помогут учителю и ученикам по- иному взглянуть на предмет математики и почувствовать себя (хотя бы немного) волшебником.

Успехов вам и вдохновения!

Математико-гуманитарные «мостики», аналогии, ассоциации.

Знание по математике тесно переплетаются со знаниями по другим, часто гуманитарным, предметам.

Особое место занимают задания на установление аналогий между математическим материалом и различными объектами из гуманитарной области и из повседневной жизни. Выявление таких тонкостей привлекают внимание школьников «далёких» от математики, придаёт им силы, вселяет надежду на дальнейшее обучение, ведь это интересно, живо, нестандартно.

Неудивительно, что такие аналогии и ассоциации существуют, т.к. источник всего математического знания- сама жизнь.

Аналогии в математике

« Я больше всего дорожу аналогиями.

Они знают все секреты природы,

И ими меньше всего следует пренебрегать в геометрии»

Ян Каплер

Аналогия (греч.)- соответствие, сходство. Приведём аргументы, которые позволят нам обосновать необходимость использования заданий на установление аналогий и ассоциаций.

Итак, первое: межпредметные аналогии помогают интегрировать знания.

Второе: приблизить предмет математики к школьнику, сделать его разным и близким, перевести правила, теоремы, задачи на язык образов, символов, эмоций.

В- третьих: работа по установлению ассоциаций способствует развитию образной памяти, обороты мышления, воображения.

Кроме того, упражнения по нахождению одинаковых понятий в различных науках (гипербола (мат.)- гипербола (литерат.)) помогают найти их объединяющий стержень, приблизить математику к условиям реальной жизни и возникающих в ней задач. Межпредметные связи, творческое мышление, ассоциативное мышление,- всё это ведёт к собственным открытиям.

Литературные метафоры математики

1. Аксиома = ясно как дважды два.

2. Метод от противного = не было бы счастья, да несчастье помогло.

3. Параллельные прямые = небо и земля.

4. Отрезок = было бы начало, будет и конец.

5. Прямая = дорога без начала и конца.

6. Луч = солнечный луч, небо вокруг.

7. Круг и шар = Загадка: без окон, без дверей полга горница людей.

8. Наклонная и её проекция = предмет, приставленный под наклоном к стене,- это наклонная.

9. Куб = кристаллы соли имеют форму куба.

10. Сравнение отрицательных чисел = из двух зол выбирай меньшее.

11. Область допустимого значения (ОДЗ) = каждый гриб в руки берут, да не каждый в кузов кладут.

12. Прямая пропорциональность = много снега - больше хлеба.

13. Обратная пропорциональность = тише едешь - дальше будешь. Дальше положишь- ближе возьмёшь. Меньше знаешь - крепче спишь.

14. Подобные слагаемые = масть к масти подбирается. Сытый голодному не товарищ.

15. Модуль числа = нет худа без добра.

16. Посторонний корень = пятое колесо к телеге.

17. Прямая и обратная теоремы = ты - мне, я - тебе.

18. Доказательство теоремы = не верь глазам своим. (Надо доказать!)

19. Дискриминант = скажи мне, кто твой друг, и я скажу, кто ты.

D 0 – 2 корня.

D 0 – корней нет.

D = 0 – 2 совпадающих корня.

20. Разные способы решения одной задачи = два ботинка на одну ногу.

Межпредметные связи

1. Обыкновенные дроби – музыка, деление пирога.

2. Пропорции, % - биология, труд, ИЗО, домоводство.

3. Масштаб- география.

4. Векторы – алгебры, физика, информатика.

5. Преобразование фигур - биология, рисование, литература.

6. Квадратные уравнения- физика, литература ( О. Хайям)

7. Прямая и обратная пропорциональность- физика, литература.

8. S круга - физика, астрономия.

9. Система координат - география, астрономия.

10. Элементы теории вероятности - биология.

11. Решето Эратосфена - история.

12. Теорема Пифагора, Фалеса, Виета - история.

13. Относительная погрешность – физика, статистика.

14. Проекция наклонной - геометрия, физика.

15. Координатная плоскость – география.

16. Процентное отношение вещества - химия.

17. Гомотетия – рисование, география.

18. Доли, дроби – музыка.

19. Формулы - физика, химия.

20. Куб, параллелепипед - черчение, физика, химия.

Математика 5 класс

1. Не путать понятия число и цифра.

С помощью их составляют

Цифра Число

Буква Слово

Цифры используют для записи слов так же, как буквы для записи слов. Иногда цифра носит роль числа так же, как буква роль слова. Например: буква (слово) Я или цифра (число) 7.

2. 11= 1+10 (один на дцать)

3. «Говорящие приставки»

ЗАПОМНИТЕ некоторые приставки, котрые помогут выучить единицы измерения величины.

Кило = 1000 1кг= 1000г килограмм

1км= 1000м километр

Санти = 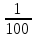1м= 100см сантиметр

Деци = 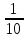1м= 10дм дециметр

Милли = 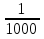1м= 1000мм миллиметр

4. Периметр (от латинского «Пери»- вокруг. Периметр - измерение в единицах длины).

5. Треугольник – ТРИ угла, вершины.

- существует такой музыкальный инструмент.

6. Луч – ассоциация с лучом о прожектора (есть начало, а конца нет)

Отрезок – «отрезали» есть 2 конца.

Шкалы и координаты

1. «Цена деления» - это понятие можно ассоциировать с длиной шага.

2. Координатный луч имеет свои три особенности, которые можно запомнить с помощью:

начало

единичный отрезок

направление

ННЕ -

S квадрата равна a в квадрате Sкв = а²

V куба равен а в кубе Vкуба = a³

Прямоугольный параллелепипед – в жизни это обычная коробка, комната, шкаф…

Ребро - как кость скелета - служит для построения каркаса.

Грань – грани граненого стакана – это уже плоскость.

Окружность ассоциируется с кольцом

Круг – ассоциация – монета

Эллипс – овал

Шар – ассоциация с мячом

Сфера- ассоциация с резиной (каркасом мяча)

Знаменатель («земля» - внизу)

Числитель («чистое небо»- вверху)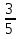

Дробь – «дробить»

Округление чисел

Правило «пятёрки» (начиная с 5, идёт увеличение на 1)

Скорость сближения

+

Нахождение V сближения зависит от направления движения.

V₂

V₁

V сближения = V₁ + V₂

Движение в двух направлениях, знак в формуле из двух чёрточек «+»

V₂

V₁

V сближения = V₁ – V₂

Движение в одном направлении, знак одна черта «-» (Из большего вычесть меньшее)

Действия с десятичными дробями

+ -

При записи в столбик запятая под запятой,

разряд под разрядом

19,124

17,89

1,234

1 8,34

0,0017

Х

х

При записи в столбик «равнение по правому краю»

Формулы

S= V ^x t Путь = работа

A= P ^x t Скорость = производительность

1 процент с латинского pro centum.

o

t

Существует история о том, откуда возник знак %. В далёкие времена наборщица текста спешила, и вместо принятого тогда написания процентов в виде С по ошибке набрала %

Виды углов

Обычно путают прямой угол с развёрнутым.

180^о

- от слова «развернуть».

Кстати сказать, не забывайте известное понятие «биссектриса» - это крыса, которая бегает по углам и делит угол пополам.

Угол 45^о можно начертить без транспортира (на клетчатой бумаге по диагонали клетки)

Тогда 135^о= 90⁰+ 45^о тоже реально начертить без транспортира.

Математика 6 класс

1. Делитель а – « он делит а»

Все делители а начинаются с 1, закончатся a 1 делитель a а

2. Кратное а – « оно делится на а»

Кратное а а Самого большого числа, кратного а, нет.

3. Признаки делимости

Признак помогает установить, будет делиться число без остатка или нет.

На 2 и 5;10: ориентир на одну последнюю цифру числа

2 ^x 5 = 10 (один 0)

На 4 и 25; 100: ориентир на две последние цифры числа

4 ^x 25 = 100

На 8 и 125; 1000: ориентир на 3 последние цифры числа

8 ^x 125 = 1000

На 3 На 9

Сумма цифр данного числа кратна

Кратна 3 Кратна 9

4. НОД (72;96)= 2^x2^x2^x3 = 24

72 2 96 2 НОД подчеркнуть

36 2 48 2 одинаковые множители в разложении

18 2 24 2 чисел.

9 3 12 2

3 3 6 2

1 3 3

1

5. : =

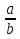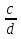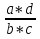
Дробь, перед которой стоит знак : , надо перевернуть

6. 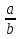от

это

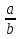Надо x от умножай на дробь ( при небрежном написании т иногда похожа на ж)

Что составляет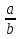

7. от ?

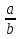?= : Если дробь рядом с?, то на неё надо делить.

8. «Правило креста» при решении пропорций

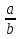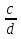⁼ получаем: a ^x d= b^x c

9. Lокружности = 2ПR²

Длина окружности измеряется в единицах длины (м, см…), зн. R в I степени

Sкруга = ПR²

Площадь измеряется в квадратных единицах, зн. R²

10. Шар = арбуз, глобус

Сфера – поверхность шара = кожура арбуза

11. Число П = 3,1415926… 3-что

1-я

4-знаю

1-о

5-круге

12. -2 -5 читать удобно: -2 да -5

Знак + и – относить к числу, перед которым он стоит

-2-5=-7

Долг да долг = долг -2+(-5)=-7

-9+3 = -6

Должны 9 рублей, а в кармане 3 = если отдашь долг, то всё равно будешь должен 6 (в данном случае)

ЗАПОМНИТЬ! При возникновении трудностей в вычислениях, выполнить про деньги (долг и наличные)

13. При х и делении правило знаков:

- ^х - = + - : - = +

- ^x + = - - : + = -

Количество минусов нечётное, ответ с минусом.

Количество минусов чётное, ответ с плюсом.

14. Раскрытие скобок

Перед () минус, значит у числах в скобках менять знаки

Минус = менять

a-(b-c+d)= a-b+c-d

15. Координатная плоскость

x

y

А

0

Чтобы отметить координаты точки А(3;2) встань в 0. Далее представь ситуацию доставки груза на другой этаж, для этого надо: 1) сначала подойти к лестнице на данном этаже или

2) подняться по лестнице вверх или спуститься вниз или

0(о;о) – начало отсчёта (озеро во Франции –Оо)

А (x;y) – сначала движение по оси оx, затем по оси oy

Ось ox = усталый человек говорит OX, и стремится занять горизонтальное положение.

Ось oy = «Ух –ты» - говорим, восхищаясь, поднимаем большой палец кулака вверх.

16. Уравнение вида |x| = а

а О , то корней нет

а = О , то корень один X=О

а , то 2 корня: x = а

17. Решение задач на прямую и обратную пропорциональность

15 кг- 8 деталей 15 машин- 8 минут

45 кг- x деталей 45 машин- x минут

I стрелку в любом направлении ставим в том столбике, где всё известно. О направлении стрелки в другом столбце думать по ситуации задачи прямая пропорциональность, то стрелки в одном направлении. Или

Обратная пропорциональность стрелки в разных направлениях: Или

= =

При составлении пропорции «иди по стрелкам»

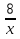
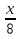
! В кратких записях величина под величиной: (кг под кг; мин. под мин.; % под %)

! В I строке говорится про I и ту же ситуацию, во II строке про II ситуацию!

Алгебра 7 класс

1. 2⁵=32 (на конце 2-чётное, 3+2=5)

2¹⁰=1024

2. 6x=3 В подобных случаях многие путают, что на что делить.

X= 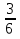= 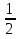Запомни так: «то, что без буквы, делить на то, что рядом с буквой»

3. 7 10 24,5

В двойном неравенстве углы знаков смотрят влево. Обратить внимание, что числа стоят по возрастанию.

4. x 0 – число положительное

X 0- число отрицательное

Х 0- число не отрицательное (усложнение в знаке, усложнение в словах)

X 0- не положительное (усложнение в знаке, усложнение в словах)

5. Хотя бы один- означает один или больше.

6. Союз «и» - в математике означает «вместе»

Союз «или» - означает объединение

И = = система Или = [ = совокупность

7. О*x = 5 O*x = О

Ответ: корней нет Ответ: x- любое число (множество корней)

Как не спутать?

X+8,2

В уравнении О^x x= 0 можно откинуть x, то получится ОО, а это похоже на знак бесконечности.

8. 324x – 1 на 9

Как составить уравнение? Смотри на знак неравенства. Уголок знака всегда смотрит на меньшее

Возможные ситуации: 1) = + - самая удобная

2) - =

3 + 4x

3) - =

9. 16,7 – x в 8 раз

Уголок на меньшее. Уравнение можно составить так:

1) x =

2) =

3) =

10. При решении задач верно и удачно составленная краткая запись- половина успешного решения.

11. y= f(x)

y

y- функция («y » есть в слове функция)

x

стрелки показывают, как смотреть по осям

0

y

y

12. как определить: какой график изображён: возрастающей функции или убывающей функции?

0

x

Ответ: смотри на оси OX тогда по прямой глаз движется, значит функция возрастающая.

Возрастает = «поднимаемся в гору»

x

Изображён график убывающей функции, т.к., смотрим по оси ОX и видим, что взгляд «катимся с горки»

0

13. Что значит слово «очевидно» - оченьвидно (очень видно)

14. Не менее a означает «больше или равно a»

15. x= ИКС - абсцисса (звук с в обоих словах)

Y= игрэк- ордината (звук р в обоих словах)

16. Ось ОX - задаётся y=0

Ось ОY – задаётся x=0

Как не запутаться?

ОX – нет буквы Y в записи, значит Y=О

ОY – в записи нет X, значит X=О

y

О в математике означает: нет ничего.

3

X=3

y

x

Y=3

18.

3

0

0

x

Как запомнить, какой оси график параллелен?

Y=3 1)отмечать 3 на той оси, где написано y=3

2) график параллелен той оси, какой буквы в записи нет.

X=3 прямая || оси oy, т.к. в записи буквы y нет

(нет x, значит график ||ox)

19. y= kx +b

b

Значение b показывает точку пересечения с осью oy

b- «Воробей на дубе»

20. y= ax² – парабола

X²= парабола (два=пара)

График похож на чашу, которая может быть и перевёрнутой.

21. y= ax³ – кубическая парабола (3=куб)

22. y= 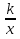- гипербола (в русском языке есть термин гипербола = преувеличение. Чем меньше x, тем больше значение y)

23. a^m x aⁿ = a^m+n x похоже на +

a^m : a ⁿ = a^m-n : на калькуляторе : , а знак : похож на –

24. Формулы «сокращённого» умножения = «быстрого» умножения.

a² – b² = (a-b)(a+b) В скобках с минусом порядок букв тот же, что в a² – b²

(a b)² = a² 2ab+ b² - у каждого одночлена II степень

a³ - a³ = (a-b)(a² + ab + b²)

в «маленькой» скобке знак – совпадает со знаком «-» в левой части, в «длинной» скобке всё «+»

a³ + a³ = (a+b)(a² - ab + b²)

в «короткой» скобке +, как в левой части, в «длинной» скобке наоборот, есть «-».

(a-b)³ = a³ – 3a² b+ 3ab² – b³ чередование знаков справа; каждый одночлен III степени

Общее для всех формул

Если в левой части формул есть (), то в правой части скобок нет, и наоборот.

Алгебра 8 класс

ax+ bx+ l

cx- dx+m

1. При сокращении дробей вида помнить правила:

-начинай преобразовывать-то, что проще (выносить за скобки, группировать)

-числитель подскажет, что делать в знаменателе и наоборот

-надо сократить = значит должно появиться что-то одинаковое в числителе и знаменателе

2. При + и – дробей надо находить НОЗ , при этом помнить:

НОЗ находим по принципу:

-всего понемногу

-одинаковое берём 1 раз

+

=

. . . . . . .

+

a

b-c

-

a

=

a(b-c)

. . . . . . .

x-2 x+2 (x-2)(x+2)

. . .^{. . . . . . . . . . .}

+

=

Берём букву в наивысшей степени из приведённых

a⁷

a⁷

a⁵

3. При нахождении дополнительных множителей дробей вспомни «кодовый замок» на дверях

b(a+5)(c-4)

c-4

a+5

=

-

b

+

НОЗ= b(a+5)(c-4) = код из трёх цифр

(b(c-4))

Тогда, чтобы войти в «I дверь» (найти дополнительный множитель I дроби) надо нажать ещё b(c-4)

=

b(c-4)

(a+5)

a+5

Аналогично, чтобы «войти во II дверь», надо ещё нажать (a+5)(c-4), т.к. b уже нажали.

«Вход в III дверь»= нажали ещё (a+5)b, т.к. (c-4) уже введено.

4. Не стоит путать понятия

Сократить и взаимно уничтожить

Сокращают дробь (когда числа «на разных этажах» )

16(x-8)⁵ = 4(x-8)⁴

12(x-8) 3

Взаимно уничтожить можно слагаемые, ( когда числа с противоположными знаками на «одном этаже»)

=

3-x+x 3

12+ 2x-12 2x

5. + и - , как конечные действия, это запрет к сокращению дробей.

X+8 нельзя сокращать ни на x, ни на 4, ни на 2

4x-10 + и – запрещают

Ассоциируйте + и – с «оголёнными» проводами, которые голыми руками не трогают!

6. x не отрицательное число, значит положительное или О

«не» отрицательная частица, значит получим , кроме того «не» усложняет понятие, значит идёт усложнение знака x О

7. «не положительное» число x. Слово «не» означает противопоставление положительному числу, значит О, но усложнение в формулировке даст усложнение знака x О.

8. Арифметический квадратный корень

Под знаком радикала может стоять неотрицательное число, т.е. О

= При извлечении из числа получаем только не отрицательный результат, т.е. О

9. 196 ^x 5 = 14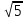 Используйте приём подчёркивания. Число 196 подчеркнули, значит из него извлекли

10. Внести под знак

= ² x

- = - ² x Отрицательному числу доступа под

нет. Он, как собачка, остаётся вне дома, на улице.

11. Вынести из- под - действие, обратное внесению под

12. (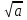)² = a 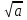² = |a|

Запомните так!

При a 0 при любом a

Были () в формуле в левой Не было скобок в левой части

части, значит в правой формулы, значит в правой

части их не будет; исчезнет части будет знак модуля;

квадрат. Исчезает квадрат.

13. Уравнения

a=0, то x=0

a 0, то корней нет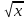

x²= a = a

a 0, то x= 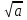a 0, то x=a²

2 корня, т.к. высшая Возводить обе части в квадрат

степень вторая, можно, если они без

причём условие существования знака «-».

корней выполнено ( a 0)

Как запомнить, когда возводить в квадрат, а когда извлекать ?

Возведение в квадрат и извлечение - это 2 обратных действия.

Если в условии был квадрат ², то придёшь к .

Если в условии был , то придёшь к возведению в квадрат²

2

14. 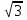11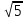 + и – невыполнимы, если подкоренные выражения разные.

Как понять? 8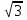 это 8 рублей

11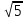 это 11 долларов

8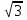+ 11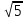= в один кошелёк положим, (т.е. соединим +), но одной валютой стать не могут ( это не будет 19 ).

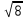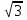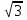НО! 8 + 11 = 19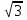 (8 рублей + 11 рублей = 19 рублей)

15. ОДЗ : = всё можно, кроме того, что нельзя.

16. Теорема Виета

ax² + bx+ c = 0 , a=1, D 0, то

x₁+x₂= -b Как запомнить?

x₁^xx₂= c -b=II коэффициент, взятый с противоположным знаком. (бэ- II буква в русском алфавите)

с- сводный член, связан с произведением корней: з-с парные согласные.

17. a^-n=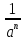

«-» превращается в , при этом aⁿ «спускается» в знаменатель.

18. x a x a

x

x

a

x

a

Штрихи от a идут вправо Штрихи от a идут влево

( скобка круглая)

ЗАПОМНИ: a a

a

x

a

Усложнение

знака

усложнение [скобка квадратная]

скобки ]

[ ]

( )

Геометрия 7 класс

1. Биссектриса – это «крыса», которая бегает по углам и делит угол пополам.

2. Медиана- от лат. «Media» -середина

3. ||-ые прямые - ассоциация: рельсы или линия земли и линия горизонта.

4. Теорема

Доказательство

Формулировка нужно, чтобы только

нужна для доказать то, о чём

решения задач гласит теорема.

5. Смежные углы- как смежные комнаты = одна стена общая, а у углов- одна сторона общая.

6. Вертикальные углы- ассоциация с (буква х)

7. Доказательство от противного или от противоположного.

8. Обратная теорема к данной. Условие заключение.

10. Свойство медианы равнобедренного треугольника

БМВ( приём запоминания- «автомобиль БМВ»)

Если в р/б треугольнике к основанию проведены:

Биссектриса Медиана Высота

Является Является Является биссектрисой и

медианой и биссектрисой и медианой.

Высотой. высотой.

11. Признаки и свойства ||-ти прямых

-Если…, то - теорема, обратная признаку

- Устанавливают ||-ть - ||-ть есть, что из этого следует

12. Внешний угол треугольника

Ассоциация: стоит человек у дома и

опирается на его стену.

13. Центр, вписанный в треугольник окружности - точка пересечения биссектрис углов треугольника.

Центр, описанный около треугольника окружности - точка пересечения серединных перпендикуляров к сторонам треугольника.

Как не перепутать? («В» похожа на «б») Опис.= сер.пер.

14. Построение

Чертёж один! Ножка циркуля встаёт в данную точку.

Угла , равного данному Биссектрисы угла

«раскрытия рта»

Надо «замерить ширину

Геометрия 8 класс

1. Схема четырёхугольников

Равнобокая

Прямоугольник

Квадрат

Ромб

Трапеция

Параллелограмм

Четырёхугольник

Прямо-угольная

2. Средняя линия треугольника

Средняя- середина сторон треугольника.

3. Построение IV пропорционального отрезка

Прилежащий катет

Гипотенуза

Искомый отрезок x сделать сначала IV членом пропорции! =

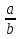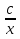
4. СOS α=

Противолежащий катет

Гипотенуза

α

SIN α =

Прилежащий катет

Гипотенуза

СOS- дОбрый=

Противолежащий катет

Гипотенуза

SIN- злой=

Противолежащий катет

Прилежащий катет

sin α

cos α

tg α = =

cos α

sin α

сtg α = = одинаковая буква сначала (с)

5. –яр и наклонная

Стена дома

Ассоциация:

Перпендикуляр = стена дома

Наклонная = лестница, прислонённая к дому

6. Не учи всю таблицу! Знай первую строку и свойства функций!

Используйте «правило снежинки»

α

30^o

2

45^o

60^o

Свойства функции

sin α

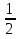
2

2

3

cos α

2

3

2

2

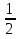
tg α

3

3

1

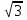
ctg α

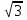
1

3

3

C

B

А

7.

C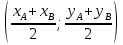

Вспомни приём деления отрезка пополам из бумаги: Сложи концы соответственно, разделишь пополам.

8. длина AB= (X_B-X_A)²+ (Y_B-Y_A)²

Длина отрезка = длинная формула.

Литература

Агеева И.Д. Занимательные материалы по математике. – М.:Сфера, 2006. – 240 с.

Баландин Б.Б. 10000 вопросов для очень умных. – М.: РИПОЛ-классик, 2007.-512 с.

Гачев Г.Д. Математика глазами гуманитария. – М.:СГУ, 2006. – 360 с.

Гузеев В.В. Гуманитарный прорыв в образовании//Народное образование. – 2006. - №2. -. С.123-129.

Дорофеев А.В. Гуманитарные аспекты преподавания математики.// Математика в школе.- 2000.-№6.

Зверев И.Д. Взаимная связь школьных предметов,- М.: знание, 1977-65с.

Лавринович К.В. – Богатство интересов – залог обучаемости//Математика в школе. – 1990. - №6

Панишова О.В. Математика для гуманитариев.- Волгоград: Учитель, 2010.-271с.

Математика 5,6 Н.Я. Виленкин – М: Мнемозина, 2007.

Алгебра 8 Н. Макарычев, под ред. С.А. Теляковского – М:Просвещение, 2009, 271 с.

Геометрия 7-9. А. В. Погорелов – М: Просвещение, 2009, 224 с.

Интернет-ресурсы

Bob Jensen’s Essay for New Faculty. – Режим доступа: http://www.trinity.edu/rjensen/000aaa/newfaculty.htm

Рифма.ком.ру & рифма.инфо/Портал «Русские рифмы».- Режим доступа: http://rifma.com.ru/

Содержание

Введение…………………………………………………………………………………………………..2

Математико-гуманитарные «мостики», ассоциации……………………………..4

Аналогии в математике…………………………………………………………………………….5

Литературные метафоры математики………….………………………………………….6

Межпредметные связи……………………………………………………………………………..8

Математика 5 класс…………………………………………………………………………………10

Математика 6 класс………………………………………………………………………………….16

Алгебра 7 класс……….………………………………………………………………………………..22

Алгебра 8 класс……..………………………………………………………………………………….28

Геометрия 7 класс….………………………………………………………………………………….35

Геометрия 8 класс….………………………………………………………………………….........37

Литература………………………………………………………………………………………………..41