ПРОГРАММА КУРСА «РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ»

1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

• Направленность дополнительной образовательной программы

Одним из направлений инновационных поисков школы является ориентация обучения на личность школьника, обеспечение возможностей её самораскрытия. При этом необходимо готовить учащихся, умеющих не просто приспосабливаться, а активно осваивать ситуации происходящих социальных перемен. Для формирования же умений в этой области необходимо создавать для детей условия, когда они должны будут действовать в нестандартной обстановке, самостоятельно находить способы решения возникающих перед ними задач, иметь возможность оценить свои знания и умения, свою подготовленность к самостоятельным действиям. Решение логических и нестандартных задач является одним из таких условий.

Ориентация современной школы на гуманизацию процесса образования и разностороннее развитие личности ребёнка предполагает, в частности, необ-ходимость гармоничного сочетания собственно учебной деятельности, в рам-ках которой формируются базовые знания, умения и навыки, с деятельностью творческой, связанной с развитием индивидуальных задатков учащихся, их познавательной активностью, способностью самостоятельно решать нестандартные задачи и т. п. Активное введение в традиционный учебный процесс разнообразных развивающих занятий, целенаправленных на развитие личностно-мотивационной и аналитико-синтетической сфер ребёнка, памяти, внимания, пространственного воображения и ряда других важных психических функций, является в этой связи одной из важнейших задач.

Программа курса включает следующие основные направления:

- формирование общеинтеллектуальных умений (операции анализа, сравнения, обобщения, выделение существенных признаков и закономерностей, гибкость мыслительных процессов);

- развитие внимания (устойчивость, концентрация, расширение объёма, переключение, самоконтроль и т. д.);

- развитие памяти (расширение объёма, формирование приёмов запоминания, развитие смысловой памяти);

- развитие пространственного восприятия и сенсомоторной координации;

- развитие учебной мотивации;

- развитие личностной сферы (в том числе снятие характерных для адаптационного периода тревожности, робости, агрессивно-защитных реакций, формирование адекватной самооценки, развитие коммуникативных способностей).

• Новизна, актуальность, педагогическая целесообразность.

Значимость указанных выше занятий в общем учебно-воспитательном про-цессе обусловлена прежде всего тем обстоятельством, что сама по себе учебная деятельность, направленная в традиционном её понимании на усвоение учащимися требований базовой школьной программы в целом, не сопряжённая в должной степени с творческой деятельностью, способна, как это ни парадоксально, привести к торможению интеллектуального развития детей. Привыкая к выполнению стандартных заданий, направленных на закрепление базовых навыков, которые имеют единственное решение и, как правило, единственный заранее предопределённый путь его достижения на основе некоего алгоритма, дети практически не имеют возможности действовать самостоятельно, эффективно использовать и развивать собственный интеллектуальный потенциал. С другой стороны, решение одних лишь типовых задач обедняет личность ребёнка, поскольку в этом случае высокая самооценка учащихся и оценка их способностей преподавателями зависит, главным образом, от прилежания и старательности, не учитывается ряд индивидуальных интеллектуальных качеств, таких как выдумка, сообразительность, способность к творческому поиску, логическому анализу и синтезу.

Таким образом, использование развивающих упражнений способствует повышению познавательной и творческо-поисковой активности детей, важное в равной степени как для учащихся, развитие которых соответствует возрастной норме, так и для тех, кто её опережает (для последних рамки стандартной программы просто тесны)

• Цели и задачи дополнительной образовательной программы

Целесообразность проведения с младшими школьниками занятий, специально направленных на развитие личностно-мотивационной и аналитико-синтетической сферы ребёнка, внимания, памяти, пространственного воображения и ряда других функций, обусловлена уникальностью данного возрастного периода, характеризующегося повышенной сензитивностью. Именно в указанный период у ребёнка наиболее интенсивно протекает процесс физиологического созревания основных мозговых структур, что даёт возможность эффективного воздействия на его интеллектуальную и личностную сферу.

Цель данного курса: создание условий для формирования и развития познавательной активности, интеллектуальных и творческих способностей младших школьников при решении логических задач.

Проведение занятий по курсу направлено на достижение следующих основных задач:

• Обучить построению логических рассуждений и выводов;

• Развивать логическое мышление, любознательность, творческое воображение, сообразительность, способность к творческому поиску, логическому анализу и синтезу, способность к абстрагированию и обобщению;

• Воспитывать общую культуру мышления, усидчивость, самоконтроль.

Кроме того, учащиеся должны приобрести практические навыки решения широкого круга логических задач, требующих творческого подхода и развивающих познавательную активность.

• Отличительные особенности данной дополнительной образовательной программы.

Введение в учебный процесс регулярных развивающих занятий, включение детей в постоянную поисковую деятельность существенно гуманизируют начальное образование. Такой систематический курс создаёт условия для развития у детей познавательных интересов, формирует стремление ребёнка к размышлению и поиску, вызывает у него чувство уверенности в своих силах, в возможностях своего интеллекта. Во время занятий по предложенному курсу происходит становление у детей развитых форм самосознания и самоконтроля, у них исчезает боязнь ошибочных шагов, снижаются тревожность и необоснованное беспокойство. Тем самым создаются необходимые личностные и интеллектуальные предпосылки для успешного протекания процесса обучения на всех последующих этапах образования.

Курс «Решение логических задач» имеет непосредственную связь со всеми основными предметами начального обучения. Так, например, более интенсивное развитие логического мышления учащихся, их внимания и памяти помогает лучше анализировать и глубже понимать читаемые тексты и изучаемые на уроках русского языка правила, свободнее ориентироваться в закономерностях окружающей действительности, эффективнее использовать накопленные знания и навыки на уроках математики, а формирование у школьников пространственного восприятия и конструкторских навыков способствует более эффективной деятельности на уроках труда.

Во время реализации этой программы отметок не ставится, чем создаются комфортные условия для успешного протекания процесса обучения на всех последующих этапах обучения. Это ещё одно из отличий программы.

• Возраст детей, участвующих в реализации дополнительной образовательной программы

Программа дополнительного образования «Решение логических задач» предназначена для обучающихся 1-4 классов, в возрасте 7-11 лет. Занятия проводятся в учебном кабинете, закрепленном за классом. Курс может вести как классный руководитель, так и любой другой учитель начальных классов.

• Сроки реализации дополнительной образовательной программы

Курс условно разделён на 4 взаимосвязанных этапа, различающихся типом и уровнем сложности используемых заданий и упражнений.

Стандартная продолжительность этапа – один учебный год. Соответственно, курс в целом занимает (при условии проведения одного занятия в неделю) 4 года.

• Формы и режим занятий

Занятия по курсу «Решение логических задач» целесообразно проводить один раз в неделю за счёт часов школьного компонента, предназначенных для общеразвивающих занятий.

Курс построен так, что основными формами работы являются индивидуальная, групповая и фронтальная.

Оптимальным вариантом являются развивающие занятия именно в рамках отдельного специального курса. Это позволяет повысить личностно-мотивационный настрой школьников и их заинтересованность благодаря объединению различных по направленности заданий единым сюжетом. Дети успешно воспринимают такие занимательные, богатые эмоциями уроки несмотря на то, что выполнение отдельных заданий представляет для них существенные трудности.

• Ожидаемые результаты и способы определения их результативности

По итогам реализации программы учащиеся должны:

• знать основные подходы к решению логических задач;

• проводить логические рассуждения и делать выводы;

• применять навыки творческой деятельности и повышение познавательной активности в учебном процессе;

• грамотно обоснованно мотивировать свои действия, опираясь на законы логики, применять их при решении логических задач, четко излагать свои мысли

• развивать способность к абстрагированию и обобщению;

• совершенствовать математические (количественные, временные, прост-

ранственные) представления;

• усвоить простейших приёмов эффективного восприятия и запоминания

вербальной и визуальной информации;

достигнуть высокого уровня развития наглядно-образного мышления и

создания фундамента для эффективного последующего развития абстракт-

но – логического мышления.

• Формы проведения итогов реализации дополнительной образовательной программы

Для определения результативности реализации программы и повышения мотивации и самооценки учащихся целесообразно периодически проводить:

• Олимпиады

• Конкурсы

• Интеллектуальные игры

• Диагностика

и направлять учащихся для участия в мероприятиях различного уровня по данному профилю.

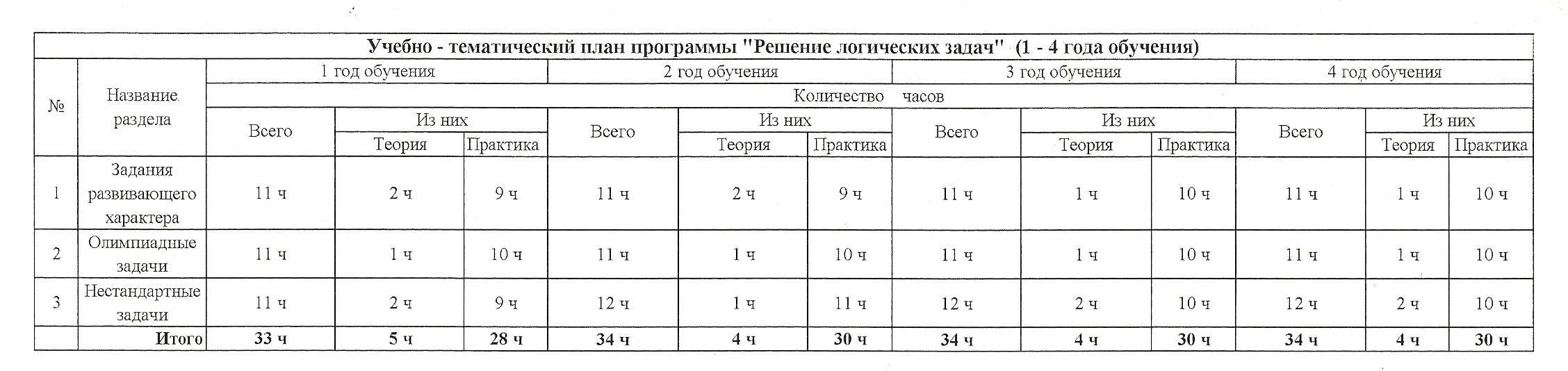
2. УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

Содержание курса включает три основных раздела:

1. Задания развивающего характера.

2. Олимпиадные задачи.

3. Нестандартные задачи.

В программе указано примерное количество часов на изучение каждого раздела. Учитель может самостоятельно распределять количество часов по темам программы, опираясь на собственный опыт и имея в виду подготовленность учащихся и условия работы в данном классе.

ПРОГРАММА

1. КЛАСС (33 ч)

ЗАДАНИЯ РАЗВИВАЮЩЕГО ХАРАКТЕРА (11 ч)

Задания на развитие памяти, внимания, воображения, логики и мышления. Задачи – загадки. Затейные задачи. Геометрические головоломки. Игра «Танграм». Ребусы «Сложи и вычти», «Распредели по группам», «Выдели признаки».

ОЛИМПИАДНЫЕ ЗАДАЧИ (11 ч)

Задачи подготовительного тура. Геометрические задачи. Задачи на планирование действий. Занимательные задачи со сказочным сюжетом. Задачи на движение, на смекалку. Задачи повышенной трудности и повышенной сложности.

НЕСТАНДАРТНЫЕ ЗАДАЧИ (11 ч)

Логогрифы. Числовые задачи – загадки. Установи закономерность. Продолжи последовательность. «Что? Где? Когда?». Пропущенное число. Зашифрованная переписка. Безмерные линейки. Задачи на движение. Самые, самые… Пирамида.

2. КЛАСС (34 ч)

ЗАДАНИЯ РАЗВИВАЮЩЕГО ХАРАКТЕРА (11 ч)

Задания на развитие логического мышления. Геометрические головоломки. Игра «Танграм». Ребусы «Сложи и вычти». Магические квадраты. Волшебные палочки. Семь раз отмерь и один раз отрежь. Конструктивные задачи. Математическая рыбалка. Логическое домино. Математические фокусы.

ОЛИМПИАДНЫЕ ЗАДАЧИ (11 ч)

Задачи подготовительного периода. Геометрические задачи. Комбинаторные задачи. Задачи на планирование действий. Циферблат. Задачи на движение. Занимательные задачи со сказочным сюжетом. Задачи повышенной сложности. Задачи – ловушки.

НЕСТАНДАРТНЫЕ ЗАДАЧИ (12 ч)

Задачи Г. Остера. Путешествие во времени. Числовые задачи – загадки. За-кономерности, последовательности. «Что? Где? Когда?» Вставь пропущенное число. Зашифрованная переписка. Безмерные линейки. Аналитические задачи. Шестиклеточный логикон. Математические фокусы. Сказки – загадки.

3 КЛАСС (34 ч)

ЗАДАНИЯ РАЗВИВАЮЩЕГО ХАРАКТЕРА (11 ч)

Логические упражнения. Числовые фигуры. Логическое домино. Лишнее число. Волшебные палочки. Числовые ребусы. Ребусы «Умножить и разделить». Вычислительные машины. Задачи на сообразительность. Логические слова. Математические лабиринты.

ОЛИМПИАДНЫЕ ЗАДАЧИ (11 ч)

Задачи на разминку. Задачи на смекалку. Комбинаторные задачи. Геометрический конструктор. Задачи на движение. Задачи на развитие пространственной ориентации. Индивидуальные задания. Парные задания. Групповые задания.

НЕСТАНДАРТНЫЕ ЗАДАЧИ (12 ч)

Логогрифы. Математические фокусы. Сказки – загадки. Математический калейдоскоп. Превращение фигур. Дорисуй девятое. Аналитические задачи. Найди ошибку. Задачи с несколькими способами решения. Шестиклеточный логикон. Пирамида.

4 КЛАСС (34 ч)

ЗАДАНИЯ РАЗВИВАЮЩЕГО ХАРАКТЕРА (11 ч)

Логические задачи. Числовые ребусы. Волшебные палочки. Логические слова. Задачи на сообразительность. Математические лабиринты. Задачи – шутки. Числовые фигуры. Игра «Танграм». Магические фигуры.

ОЛИМПИАДНЫЕ ЗАДАЧИ (11 ч)

Задачи подготовительного этапа. Задачи на развитие пространственной ориентации. Геометрические задачи. Задачи на смекалку. Комбинаторные за-дачи. Индивидуальные задания. Парные задания. Групповые задания. Резервные задачи.

НЕСТАНДАРТНЫЕ ЗАДАЧИ (12 ч)

Математические игры и фокусы. Загадки в цифрах. Исключи лишнее. Нарисуй без отрыва. Задачи на простейшее умозаключение. Задачи на развитие логической операции отрицания. Задачи Г. Остера. Безмерные линейки. Логические задачи с величинами. Аналитические задачи.

ПРИМЕРНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ.

1 КЛАСС (33 ч)

Задания развивающего характера – 11 ч

1

Задания на развитие памяти.

2

Задания на развитие внимания.

3

Задания на развитие воображения.

4

Задания на развитие логики и мышления.

5

Задачи – загадки.

6

Затейные задачи.

7

Геометрические головоломки.

8

Геометрические головоломки. Игра «Танграм».

9

Ребусы «Сложи и вычти».

10

Задания «Распредели по группам».

11

Задания «Выдели признаки».

Олимпиадные задачи – 11 ч

12

Задачи подготовительного тура.

13

Задачи подготовительного тура.

14

Геометрические задачи.

15

Задачи на планирование действий.

16

Занимательные задачи со сказочным сюжетом.

17

Занимательные задачи со сказочным сюжетом.

18

Задачи на движение.

19

Задачи на смекалку.

20

Задачи повышенной трудности.

21

Задачи повышенной сложности.

22

Резервные задачи.

Нестандартные задачи – 11 ч

23

Логогрифы.

24

Числовые задачи – загадки.

25

Задания «Установи закономерность».

26

Задания «Продолжи последовательность».

27

Что? Где? Когда?

28

Пропущенное число.

29

Зашифрованная переписка.

30

Безмерные линейки.

31

Задачи на движение.

32

Самые, самые …

33

Пирамида.

2 КЛАСС (34 ч)

Задания развивающего характера – 11 ч

1

Задания на развитие логики мышления.

2

Геометрические головоломки.

3

Игра «Танграм».

4

Ребусы «Сложи и вычти».

5

Магические квадраты.

6

Волшебные палочки.

7

Семь раз отмерь и один раз отрежь.

8

Конструктивные задачи.

9

Математическая рыбалка.

10

Логическое домино.

11

Математические фокусы.

Олимпиадные задачи – 11 ч

12

Задачи подготовительного этапа.

13

Задачи подготовительного этапа.

14

Геометрические задачи.

15

Геометрические задачи.

16

Комбинаторные задачи.

17

Задачи на планирование действий.

18

Циферблат.

19

Задачи на движение.

20

Занимательные задачи со сказочным сюжетом.

21

Задачи повышенной сложности.

22

Задачи – ловушки.

Нестандартные задачи – 12 ч

23

Задачи Г. Остера.

24

Путешествие во времени.

25

Числовые задачи – загадки.

26

Закономерности, последовательности.

27

Что? Где? Когда?

28

Задания «Вставь пропущенное число».

29

Зашифрованная переписка.

30

Безмерные линейки.

31

Аналитические задачи.

32

Шестиклеточный логикон.

33

Математические фокусы.

34

Сказки – загадки.

3 КЛАСС (34 ч)

Задания развивающего характера – 11 ч

1

Логические упражнения.

2

Числовые фигуры.

3

Логическое домино.

4

Лишнее число.

5

Волшебные палочки.

6

Числовые ребусы.

7

Ребусы «Умножь и раздели».

8

Вычислительные машины.

9

Задачи на сообразительность.

10

Логические слова.

11

Математические лабиринты.

Олимпиадные задачи – 11 ч

12

Задачи на разминку.

13

Задачи на разминку.

14

Задачи на смекалку.

15

Комбинаторные задачи.

16

Комбинаторные задачи.

17

Геометрический конструктор.

18

Задачи на движение.

19

Задачи на развитие пространственной ориентации.

20

Индивидуальные задания.

21

Парные задания.

22

Групповые задания.

Нестандартные задачи – 12 ч

23

Логогрифы.

24

Математические фокусы.

25

Сказки – загадки.

26

Математический калейдоскоп.

27

Превращение фигур.

28

Дорисуй девятое.

29

Аналитические задачи.

30

Аналитические задачи.

31

Найди ошибку.

32

Задачи с несколькими способами решений.

33

Шестиклеточный логикон.

34

Пирамида.

4 КЛАСС (34 ч)

Задания развивающего характера – 11 ч

1

Логические задачи.

2

Числовые ребусы.

3

Волшебные палочки.

4

Логические слова.

5

Задачи на сообразительность.

6

Математические лабиринты.

7

Задачи – шутки.

8

Числовые фигуры.

9

Игра «Танграм».

10

Игра «Танграм».

11

Магические фигуры.

Олимпиадные задачи – 11 ч

12

Задачи подготовительного этапа.

13

Задачи подготовительного этапа.

14

Задачи на развитие пространственной ориентации.

15

Задачи на развитие пространственной ориентации.

16

Геометрические задачи.

17

Задачи на смекалку.

18

Комбинаторные задачи.

19

Индивидуальные задания.

20

Парные задания.

21

Групповые задания.

22

Резервные задачи.

Нестандартные задачи – 12 ч

23

Математические игры и фокусы.

24

Загадки в цифрах.

25

Задания «Исключи лишнее».

26

Задания «Нарисуй без отрыва».

27

Задачи на простейшее умозаключение.

28

Задачи на простейшее умозаключение.

29

Задания на развитие логической операции отрицания.

30

Задачи Г. Остера.

31

Безмерные линейки.

32

Логические задачи с величинами.

33

Логические задачи с величинами.

34

Аналитические задачи.

3. МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ

Методическое обеспечение программы состоит из УМК (дидактический, раздаточный материал, наглядные и методические пособия, тетради с печатной основой), который подразумевает следующие формы работы по разделам:

1 раздел «Задания развивающего характера» - беседа, игра, индивидуальная и групповая работа;

2 раздел «Олимпиадные задачи» - беседа, игра, индивидуальная работа, соревнование, конкурс;

3 раздел «Нестандартные задачи» - беседа, игра, индивидуальная, групповая и фронтальная работа, конкурсы, КВН, интеллектуальный марафон.

«Решение логических задач»

Занимательные вопросы

Аня жила ближе к школе, чем Валя. Кто из них жил от школы дальше?

Математические фокусы

Как из пяти спичек получить восемь, не ломая их?

Задачи на смекалку

Я провел у бабушки понедельник, вторник, среду и четверг, а моя сестра в ту неделю - среду, четверг, пятницу и субботу. Сколько всего дней гостили мы у баб} ки? (6 дней)

Ребусы

ВИЗ НА 100 Л ПРО 10OP

Задача на смекалку

1. Сколько получится, если из наименьшего двузначного числа вычесть на большее однозначное? (10-9 =1)

2. Сколько получится, если из числа, выраженного тремя единицами второго раз­ряда, вычесть число, выраженное пятью единицами первого разряда? (30 -5 = 25)

Задача-шутка

1. Что тяжелее - килограмм ваты или килограмм железа?

2. Два отца и два сына съели 3 апельсина. Сколько апельсинов съел каждый из них? (По одному)

МАТЕМАТИЧЕСКИЕ ИГРЫ (соревнования)

Игра «Бегущие минутки»

Вопросы 1-й команде:

1. Сколько пальцев на руке?

2. Сколько букв в русском алфавите?

3. Сколько букв в слове школа!

4. Сколько слогов в слове Вуратино!

5. Сколько дней в неделе?

6. Сколько сторон у квадрата?

7. Сколько сторон у шестиугольника?

8. Сколько десятков в числе 18?

9. Сколько отдельных единиц в числе 15?

1. 
   

   Как назвать число, в котором 10 десятков?

2. Как называется результат при сложении?

3. Сколько см в двух дм?

Вопросы 2-й команде:

1. 
   

   Сколько пальцев на двух руках?

2. Сколько гласных букв в русском алфавите?

3. Сколько слогов в слове карандаш*?

4. Сколько букв в слове урок!

5. Сколько месяцев в году?

6. Сколько сторон у прямоугольника?

7. Сколько сторон у пятиугольника?

8. Сколько десятков в числе 11?

9. Сколько отдельных единиц в числе 16?

10. Как назвать число, в котором 7 десятков?

11. Как называется результат при вычитании?

12. Сколько дм в сорока см?

Игра «Угадай фигуру»

Вопросы 1-й команде:

1. 6 одинаковых граней, 12 одинаковых ребер, 8 вершин. (Куб.)

2. 3 угла, 3 разные стороны. (Разносторонний треугольник.)

3. 3 стороны, 3 угла, один из которых прямой. (Прямоугольный треугольник.)

4. 4 прямых угла, 4 стороны, противоположные стороны равны. (Прямоугольник.)

5. 3 стороны, 3 угла, 2 из которых прямые. (Вопрос-ловушка.)

6. 3 угла, 3 стороны, все стороны равны. (Равнобедренный треугольник.)

Вопросы 2-й команде:

1. 4 угла, 4 стороны, противоположные углы равны, стороны равны. (Ромб.)

2. 3 стороны, 3 угла, один из которых тупой. (Тупоугольный треугольник.)

3. 4 стороны, 4 угла, все углы прямые. (Прямоугольник.)

4. 4 прямых угла, 4 стороны, все стороны равны. (Квадрат.)

5. 4 стороны,4 острых угла. (Вопрос-ловушка.)

6. 3 угла, 3 стороны, все стороны равны. (Равносторонний треугольник.)

Математические квадраты как средство развития умения

вычислять и рассуждать

8

18

4

6

10

14

16

2

12

12

27

9

18

15

21

24

3

18

Задание: докажите, этот квадрат не математический

Задание: в математиче­ском квадрате суммы чи­сел по любым вертика­лям, по любым горизон­талям равны одному и тому же числу. Проверь­те, будет ли данный

квадрат математическим.

12

22

8

10

14

18

20

6

16 |

6

4

7

10

8

6

*

16

2

Задание: в математиче­ском квадрате суммы чи­сел по любым вертика­лям, по любым горизон­талям равны одному и тому же числу. Найдите это число.

Задание: дан квадрат, в котором в некоторые клеточки вписаны числа. Вставьте числа 3, 5, 8, 9, 11 так, чтобы получился магический квадрат.

Задание: дан математи­ческий квадрат. Докажи­те, что в клеточке со звездочкой (*) не может стоять число 32.

8

18

4

6

10

16

2

12

8

14

20

4

9

А

3

5

Б

8

1

В

Задание: дан мате тический квадрат, кое число должно ять в пустой клетке?

Задание: дан квадра, в котором в некоторых клеточки вписаны числа. Вставьте числа ( 10, 12, 16, 18, 22 так, чтобы получился магический квадрат.

Задание: дан матема­тический квадрат. Най­дите сумму чисел, ко­торые «спрятались» за буквами А, Б, В.

8

18

А

6

10

Б

Г

2

В

Задание; дан математический квадрат. Найдите сумму чисел А + Б + В + Г.

Занимательная геометрия

Изобрази человечка с помощью кругов и отрезков.

Анаграммы

У кого из этих животных 38 ног? ЦАРИУК, ТОМЕГЕБ, АКР.

У кого их этих животных 10 глаз? ВРООКА, КВАИПЯ НОЕЛЬ.

Палиндром

Закончи палиндром:

Около Миши ....

На доме ч

Шороху дуба

Игра «Спрятанная поговорка»

Поставь названия месяцев в правильном порядке и узнаешь поговорку.

«Эльфийские игры»

Впишите в пустые клеточки буквы так, чтобы получились значимые слова.

Е

Л

ь

Е

Л

ь

Е

Л

ь

Е

л

ь

Е

л

ь

Е

л

ь

Е

л

ь

Е

л

ь

Е

л

ь

Е

л

ь

Е

л

ь

Е

л

ь

ДИАГНОСТИКА СТЕПЕНИ ВЛАДЕНИЯ ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ

Способность выделять существенное

Учитель предлагает ряд слов, в каждом из которых 5 дается в скобках, а одно перед ними. Ученики должны исключить из скобок, т.е. выделить, 2 слова, наиболее существен­ные для слова, стоящего перед скобками.

• Спорт (медаль, оркестр, состязание, победа, стадион).

• Война (пушки, аэроплан, сражения, солдаты, ружья).

• Пение (звон, голос, искусство, мелодия, аплодисменты).

• Город (автомобиль, здание, толпа, улица, велосипед).

• Лес (лист, яблоня, охотник, дерево, кустарник).

Обработка результатов: ученики, которые правильно справились с заданием, оче­видно, обладают умением выделять существенное, т.е. способны к абстрагированию.

Сравнение

Каждый ученик на листе бумаги должен написать черты сходства - слева, а справа -черты различия названных предметов, понятий.

• Книга - тетрадь.

• Дождь - снег.

• Лошадь - корова.

Обработка результатов: составляется общий список черт сходства и различия на­званных предметов, затем устанавливается, какую часть из этого списка сумел написать ученик. Доля названных учеником черт сходства и различия из общего числа черт в про­центах - это уровень развития у него умения сравнивать.

Обобщение

Предлагается 2 слова. Ученику нужно определить, что между ними общего.

• Школа - учитель.

• Дождь-град.

• Нос - глаз.

Классификация

Эта методика также выявляет умение обобщать.

Даны пять слов. Четыре из них объединены общим признаком. Пятое слово к ним не подходит. Нужно найти это слово.

1. треугольник, отрезок, длина, квадрат, круг

2. молоко, сыр, сметана, простокваша, мясо

3. футбол, хоккей, волейбол, плавание, баскетбол

4. дуб, дерево, ольха, тополь, береза

5. секунда, час, год, вечер, неделя

Теоретический анализ с помощью анаграммы

Предлагаются анаграммы. Надо по анаграммам найти исходные слова.

осокл исал оголав абарн

Обработка результатов: 1-я группа - у них отсутствует теоретический анализ, 2-я группа - ученики быстро находят ответы, обнаружив общее правило.

Анализ отношений понятий (аналогия)

Даны три слова. Первые два находятся в определенной связи. Между третьим и од­ним из предложенных пяти слов существуют такие же отношения. Нужно найти четвертое слово.

Песня : композитор = самолет : ?

а) аэродром

б) горючее

в) конструктор

г) летчик

д) истребитель

Эта методика позволяет выявить у учащихся умение определять отношения межд\ понятиями или связи между понятиями:

а) причина - следствие

б) противоположность

в) род - вид

г) часть - целое

д)функциональные отношения

Изучение скорости протекания мыслительных процессов

Использование метода, суть которого состоит в заполнении пропущенных букв в слове;

Д_р_в_, р_ка, г_ра, п_ле, п_ро,к_са

Оценка результатов

Тесты

Высокий уро-

Выше

Средний

Ниже

Низкий

вень

среднего

уровень

среднего

уровень

Анаграмма

Существенное

Сравнение

Классификация

Обобщение

Аналогия

5 5 5 5 5 9-10

4

4 4 4 4 7-8

3 3 3 3 3 5-6

2 2 2 2 2 3-4

0-2

За каждый правильный ответ присваивается 1 балл

Общий уровень мышления

30-35

24-29

18-23

10-17

0-9

Список использованной литературы:

1. Бабкина Н.В.Радость познания. Программа занятий по развитию познавательной деятельности младших школьников: Книга для учите-ля. – М.: АРКТИ, 2000. – 78 с.

2. Байрамукова П.У. Математика. Сборник задач 1 – 3 класс. «Через сказ-ку в мир математики». – М.: «Издат – школа 2000», 1999. – 64 с.

3. Беденко М.В. Самостоятельные и контрольные работы по математике: 1 – 4 класс. – М.: ВАКО, 2005. – 224 с.

4. Бурлака Е.Г., Прокопенко И.Н. Занимательная математика. –Донецк: ПКФ «БАО», 1997. – 352 с.

5. Калугин М.А., Новоторцева Н.В. Развивающие игры для младших школьников. Кроссворды, викторины, головоломки. Популярное посо-бие для родителей и педагогов. – Ярославль: Академия развития, 1996.- 224 с.

6. Калугин М.А. После уроков. Ребусы, кроссворды, головоломки. Попу-лярное пособие для родителей и педагогов. – Ярославль: Академия развития, 1997. – 192 с.

7. Лавриненко Т.А. Задания развивающего характера по математике: По-собие для учителей начальных классов. – Саратов: Лицей, 2003. – 192 с.

8. Левитас Г.Г. Нестандартные задачи на уроках математики в 1 – 4 классах. – М.: Илекса, 2005. – 230 с.

9. Лихтарников Л.М. Числовые ребусы и способы их решения. Для учащихся начальной школы. – СПб.: Лань, МИК, 1996. – 125 с.

10. Минскин Е.М. Игры и развлечения в группе продлённого дня: пособие для учителя. – 3-е изд. – М.: Просвещение, 1985. – 192 с.

11. Панскова Г.В. Всё дело в мыслях./Материалы Олимпиады-98 для учащихся начальных классов инновационных школ/ - Чебоксары: «КЛИО», 1998. – 48 с.

12. Русанов В.Н. Математические олимпиады младших школьников: Книга для учителя: Из опыта работы. – М.: Просвещение, 1990. – 77 с.

13. Смекалка для малышей. Занимательные задачи, загадки, ребусы, голо-воломки. Пособие для начальной школы. – М.: «Омега», 1994. – 256 с.

14. Степанова С.Ю. Сборник задач по математике для учащихся 1 – 3 классов: Пособие для учителей и родителей. – И.:«Свиток», 1996.- 72 с.

15. Тарабарина Т.И., Ёлкина Н.В. И учёба, и игра: МАТЕМАТИКА. Попу-лярное пособие для родителей и педагогов. – Ярославль: «Академия развития», 1997. – 240 с.

16. Тихомирова Л.Ф. Логика. Дети 7 – 10 лет. – Ярославль: Академия развития: Академия Холдинг, 2002. – 144 с.

17. Тихомирова Л.Ф. Математика в начальной школе: развивающие игры, задания, упражнения. Пособие для учителей начальных классов, воспи-тателей детских садов. – М.: ТЦ «Сфера», 2003. – 96 с.

18. Тонких А.П., Кравцова Т.П., Лысенко Е.А. и др. Логические игры и зада-чи на уроках математики. Популярное пособие для родителей и педагогов. – Ярославль: 2Академия развития», 1997. – 240 с.

19. Узорова О.В. Контрольные и олимпиадные работы по математике: По-собие для четырёхлетней начальной школы: 1 – 2 классы. – М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2004. – 127 с.

20. Чутчева Е.Б. Занимательные задачи по математике для младших школьников: Учебное пособие. – М.: ВЛАДОС, 1996. – 144 с.

21. Шиманская Г.С., Шиманский В.И. Логические игры и задачи. – Д.: Сталкер, 1997. – 448 с.