Шпаргалка по Математическому программированию










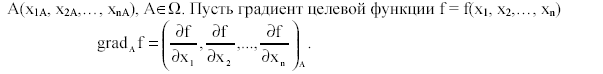
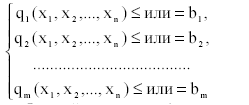
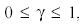
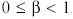
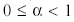
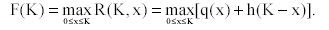



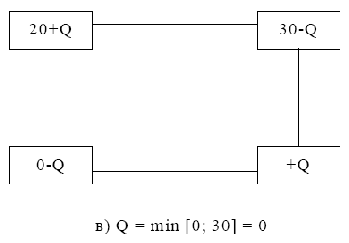






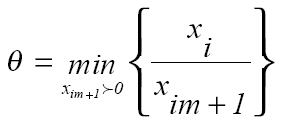









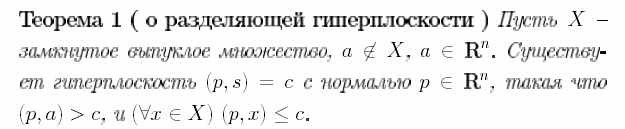
направления использования мат. моделей в экономике.
Математические модели позволяют определять оптимальные значения неизвестных параметров экономических систем, что является важным в процессе принятия решений. Математическое программирование как раз и дает аппарат, позволяющий оптимизировать процесс отбора лучших вариантов планов в процессе управления в экономических системах.
Используется в матстастике, оптимизационные методы, методы экономич. кибернетики, экспериментальные задачи.
При изучении сложных процессов и явлений в экономике очень часто применяется моделирование – вполне определенное конкретное отображение рассматриваемых характеристик изучаемого объекта. Суть его состоит в том, что изучаемое явление воспроизводится в экспериментальных условиях с помощью модели в другом временном и пространственном масштабе. Модель – это специально создаваемый объект, с помощью которого воспроизводится вполне определенные характеристики исследуемой системы с целью ее изучения. Математическое моделирование является наиболее совершенным и вместе с тем эффективным методом получения информации об исследуемом объекте. Оно представляет собой мощное средство анализа в экономике. Результаты исследования с помощью моделей будут иметь практический интерес тогда, когда построенная модель будет достаточно адекватна рассматриваемому явлению, т.е. достаточно хорошо отображать реальную ситуацию.
2. математическое програмирование как наука, его структура. Задачи оптимизации. Трудности применения классических методов оптимизации при решении экономических задач.
Математическое программирование – это раздел прикладной математики, который разрабатывает теоретические основы и методы решения экстремальных задач.
К математическому программированию относятся ряд разделов, основные из которых следующие:
1. Линейное программирование. К данному разделу относятся задачи, в которых неизвестные переменные входят в математические соотношения в первой степени.
2. Нелинейное программирование. К данному разделу относятся задачи, в которых целевая функция и (или) ограничения могут быть нелинейными.
3. Динамическое программирование. К данному разделу относятся задачи, в которых процесс решения можно разбить на отдельные этапы.
4. Целочисленное программирование. К данному разделу относятся задачи, в которых неизвестные переменные могут принимать только целочисленные значения.
5. Стохастическое программирование. К данному разделу относятся задачи, в которых содержатся случайные величины в целевой функции или ограничениях.
6. Параметрическое программирование. К данному разделу относятся задачи, в которых коэффициенты при неизвестных переменных в целевой функции или ограничениях зависят от некоторых параметров.
Для решения задач математического программирования сложно использовать классические методы нахождения экстремума т. к. в задачах математического программирования целевая функция достигает своего экстремального значения на границе области допустимых значений неизвестных переменных, а производные в граничных точках не существуют. Полный перебор допустимых точек невозможен из-за значительного их количества.
3. Понятие математической модели, виды мат. моделей
Математическая модель – это записанная в математических символах и выражениях абстракция реального явления или процесса. Математические модели экономических процессов и явлений называются экономико-математическими моделями
Модели делятся на:
линейные, в которых все зависимости описываются линейными соотношениями,
нелинейные, в которых имеются нелинейные соотношения;
стохастические, в которых учитывается случайный характер изучаемых процессов,
детерминированные, в которых учитываются усредненные значения всех параметров.
динамические модели, в которых исследуемые системы рассматриваются в развитии в течение нескольких периодов,
статические, в которых фактор времени не учитывается.
оптимизационные модели, в которых выбор осуществляется в зависимости от экстремизации некоторого критерия,
неоптимизационные, в которых критерия оптимальности нет.
макромодели (всего хозяйства в целом)
микромодели (отдельных звеньев или процессов экономики).
Виды математических моделей: линейные, нелинейные, квадратические, целочисленные, дискретные, параметрические, дробно-линейные, динамические, стохастические
4. Общая постановка задач математического програмирования.
Рассмотрим общую постановку задачи математического программирования.
Общая задача математического программирования состоит в определении оптимального значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений. Математически определение оптимального решения выражается в нахождении экстремума (max или min) функции многих переменных
Z = f (x1, x2, …, xn)
в заданной области изменения этих переменных
gi (x1, x2,…, xn)Ribi (i = 1, 2,…, m),
где Ri - один из знаков ≥, =, ≤.
5. Задача об оптимизации плана выпуска продукции. Экономическая постановка и построение математической модели задач.
Экономическая постановка:
Предприятие производит n видов продукции с использованием m видов сырья. Для производства единицы продукции используется строго определённое количество сырья того или иного вида. Сырьё каждого вида на предприятии ограничено. Предприятие получает определённую прибыль от реализации единицы продукции. Необходимо найти такой план производства продукции, при котором предприятие получит максимальную общую прибыль.
Математическая постановка:
Введём обозначения заданных параметров.
Пусть j – индекс вида продукции j = 1, n
i– индекс вида ресурсов i = 1, m
аij – затраты сырья i-го вида на производство единицы продукции j-го вида;
Аi – заданное ограничение на имеющийся объём ресурсов i-го вида;
Рj – прибыль, получаемая от реализации единицы продукции j-го вида;
Введём неизвестные переменные:
xj – объём выпускаемой продукции j-го вида.
В терминах введённых обозначений данная задача запишется следующим
образом:
z = Р1x1 + Р2x2 + … +Pnxn → max
а11x1 + а12x2 +…+ а1nxn ≤ A1
а21x1 + а22x2 +…+ а2nxn ≤ A2
…………………………….
a m1x1 + а m2x2 +…+ а m n xn ≤ Am
xj ≥ 0, j = 1, n
6. Задача о рационе. Экономическая постановка и построение математической модели задачи.
Экономическая постановка
В некотором фермерском хозяйстве производится откорм животных. Для откорма используется n видов кормов. Известно содержание питательных веществ (кальций, фосфор и др.) в единице корма каждого вида. Для полноценного питания животных необходимо потребление питательных веществ не меньше заданных количеств. Известна стоимость единицы каждого корма. Необходимо определить рацион кормления животных, при котором общие затраты на откорм будут минимальными.
Математическая постановка:
Введём обозначения заданных параметров:
j – индекс вида кормов, j = 1, n
i – индекс вида питательных веществ, i = 1, m
аij – содержание i-го питательного вещества в единице корма j-го вида;
Аi – необходимое суточное потребление питательного вещества i –го вида;
Сj – стоимость единицы кормов j-го вида.
Введём неизвестные переменные:
хj – суточный объём кормления животных j-м видом корма.
В терминах введённых обозначений данная задача запишется следующим
образом:
z = С1x1 + С2x2 + … +Сnxn → min
а11x1 + а12x2 +…+ а1nxn ≥ A1
а21x1 + а22x2 +…+ а2nxn ≥ A2
…………………………….
am1x1 + аm2x2 +…+ а mnxn ≥Am
xj ≥ 0, j = 1, n
7. Транспортная задача. Экономическая постановка и построение математической модели задачи.
Экономическая постановка:
Имеется m поставщиков однородной продукции и n потребителей этой продукции. Известны удельные затраты на доставку единицы продукции от каждого поставщика каждому потребителю. Запасы продукции у поставщиков ограничены. Известны так же потребности в продукции каждого потребителя.
Необходимо определить такой план перевозки продукции от поставщиков к потребителям, при котором общие затраты на перевозку будут минимальными.
Математическая постановка:
Введём обозначения заданных параметров:
j – индекс потребителей, j = 1, n
i – индекс поставщиков, i = 1, m
Аi – объём имеющейся продукции у i-го поставщика;
Вj – объём потребность в продукции j-го потребителя;
Cij – удельные затраты на перевозку единицы продукции от i-го поставщика j-му потребителю.
Введём неизвестные переменные:
хij – объём перевозки продукции от i-го поставщика j-му потребителю.
В терминах введённых обозначений данная задача запишется следующим образом:
z = С11x11 + С12x12 +…+С1nx1n + С21x21 +…+ Сm(n -1)xm (n-1) + Сmnxmn → min
Ограничения задачи.
I. От каждого поставщика можно вывести продукцию не более имеющегося количества:
x11 + x12 +…+ x1n ≤ A1
x21 + x22 +…+ x2n ≤ A2 (2)
…………………….
xm1 + xm2 +…+ xmn ≤ Am
II. Потребность каждого потребителя в продукции должна быть удовле-
творена:
x11 + x21 +…+ xm1 ≥B1
x12 + x22 +…+ xm2 ≥B2
……………………. (3)
x1n + x2n +…+ xmn ≥Bn
III. Условие неотрицательности: xij ≥0, i = 1, m ; j = 1, n
Часто удобно записывать математическую постановку в свёрнутом виде:
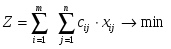
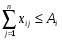 , i = 1, m
, i = 1, m 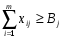 , j = 1, n
, j = 1, n
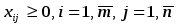
8. Задача о выборе назначениях или о назначениях. Экономическая постановка и построение математической модели задачи.
Экономическая постановка:
Имеются n видов работ и n исполнителей. Каждый из исполнителей может выполнить любую, но только одну работу. Задана себестоимость выполнения каждой работы, каждым исполнителем. Необходимо закрепить исполнителей за работой таким образом, чтобы общая стоимость выполнения работ была минимальной.
Математическая постановка.
Введём обозначения заданных параметров.
i – индекс работ, i = 1, m
j – индекс исполнителей, j = 1, n
Cij – себестоимость выполнения i-той работы j-тым исполнителем.
Введём неизвестные переменные. В данной задаче неизвестные переменные могут принимать только два значения 0 или 1. Такие переменные называются нулевыми.
1 - если за i-той работой закреплён j-тый исполнитель;
x ij =
0 - в противном случае.
В терминах введённых обозначений данная задача запишется следующим образом:
z = С11x11 + С12x12 +…+С1nx1n + С21x21 …+ С(n-1)(n -1)x(n-1)(n-1) + Сnnxnn → min
I группа ограничений.
За каждой работой должен быть закреплён только один исполнитель:
x11 + x12 +…+ x1n = 1
x21 + x22 +…+ x2n = 1
……………………..
xn1 + xn2 +…+ xnn = 1
II. группа ограничений.
Каждый исполнитель может выполнить только одну работу:
x11 + x21 +…+ xn1 = 1
x12 + x22 +…+ xn2 = 1
……………………..
x1n + x2n +…+ xnn = 1
x ij = { 0,1} i = 1, n ; j = 1, n
9. Задача о раскрое материалов. Экономическая постановка и построение математической модели задачи.
Экономическая постановка.
На раскрой поступает исходный материал одинакового размера. Его требуется раскроить на заготовки заданного размера в заданном количестве, таким образом, чтобы общие отходы были минимальными.
Математическая постановка.
Введём обозначения:
i – индекс заготовок,
Аi – необходимое количество заготовок i-того типа;
j – индекс вариантов раскроя,
Сj –размер отходов при раскрое единицы исходного материала по варианту j;
а ij – количество заготовок i-того вида при раскрое единицы исходного материала по варианту j.
Введём обозначения неизвестных переменных.
хj- количество исходного материала раскроенного по варианту j.
В терминах введённых обозначений данная задача запишется следующим образом:
z = С1x1 + С2x2 + … +Сnxn → min
а11x1 + а12x2 +…+ а1nxn = A1
а21x1 + а22x2 +…+ а2nxn = A2
…………………………….
am1x1 + аm2x2 +…+ аmnxn =Am
xj ≥ 0, j = 1, n
Применение математических моделей позволяет экономить исходные материалы до 20 %.
Математическая модель раскроя строится в два этапа.
На первом этапе производится построение вариантов раскроя, в результате которого определяются значения количества вариантов n, количества заготовок каждого вида, получаемых при различных вариантах раскроя (аij), а так же значения отходов (Сj).
Построение вариантов раскроя единицы исходного материала осуществляется в виде следующей таблицы:
№ варианта
Заготовка i1
Заготовка i2
…
Заготовка im
Отходы
Заготовки располагаются в порядке невозрастания их размеров. Построение вариантов осуществляется методом полного перебора.
10. Общая форма модели задач ЛП и ее особенности
Общая форма ЗЛП имеет вид:
Найти максимум или минимум целевой функции z:
z = С1x1 + … + Сnxn max (min)
При выполнении следующих ограничений:
а11 X1 + a12 X2 + … + а1n Xn R1 a1
а21 X1 + a22 X2 + … + а2n Xn R2 a2
………………………………………………….
am1 X1 + аm2 X2 +…+ аmnxn Rm am
хj ≥ 0, j = 1, k, k ≤ n
В общей форме каждый символ R1 , R2 ,…, Rm означает один из знаков: ≥, = или ≤ .
Общая форма модели задачи ЛП обладает следующими особенностями.
Система ограничений представлена в виде уравнений (жестких условий) и неравенств (нежестких условий).
Условия неотрицательности накладываются не на все переменные
Целевая функция стремится либо к максимуму, либо к минимуму.
11. Стандартная форма модели задач ЛП и ее особенности
Стандартная форма имеет следующий вид.
Найти максимум или минимум целевой функции z:
z = С1x1 + … + Сnxn → max (min) (1)
При выполнении следующих ограничений:
а11 Х1 + а12 Х2 + … + а1n Хn ≤ а1
а21 Х1 + а22 Х2 + … + а2n Хn ≤ а2
…………………………………………..
am1 Х1 + аm2 Х2 +… + аmn Хn ≥ аm
хj ≥ 0, j = 1, k, k ≤ n
Особенности стандартной формы модели задачи ЛП следующие:
система ограничений представлена в виде неравенств (нежестких условий)
условия неотрицательности накладываются на все переменные
целевая функция стремится либо к max, либо к min
12. Каноническая форма модели задач ЛП и ее особенности
Каноническая форма имеет вид:
Найти минимум целевой функции z:
z = С1x1 + … + Сnxn → min
При выполнении следующих ограничений:
а11 Х1 + а12 Х2 + … + а1n Хn = а1
а21 Х1 + а22 Х2 + … + а2nxn = а2
…………………………
am1x1 + аm2 X2 +… + аmn Xn = am
Xj ≥0, j = 1, n
Особенности канонической формы следующие:
Система ограничений представлена в виде уравнений (жестких условий).
Условия неотрицательности накладываются на все переменные
Целевая функция стремится к
В некоторых источниках целевая функция задачи ЛП, представленной в канонической форме, стремится к максимуму. Это делается для удобства решения задачи по алгоритму, разработанному на максимум целевой функции.
13. Возможный, допустимый, оптимальный опорный план задачи, ОДЗ задачи ЛП
Определение 1. Значения неизвестных переменных, удовлетворяющие всем ограничениям задачи линейного программирования, называются допустимыми значениями переменных или планами.
Определение 2. Множество всех планов задачи линейного программирования называется областью допустимых значений переменных (ОДЗ).
Определение 3. План задачи линейного программирования, при котором целевая функция принимает минимальное (или максимальное) значение на ОДЗ называется оптимальным.
14. Виды записей задач ЛП: развернутая, свернутая, матричная, векторная.
Модели задач ЛП могут быть записаны в различных видах.
1. Развернутый вид записи модели
Z = c1 X1 + c2 X2 + … + cn Xn → min
a11 X1 + a12 X2 + … + a1n Xn = a1,
a21 X1 + a22 X2 + … + a2n Xn = a2,
……………………………………………
a m1 X1 + am2 X2 + … + amn Xn = am,
Xj ≥ 0, j = 1, n.
2. Свернутый вид:
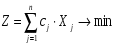
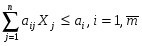 ,
,
Xj ≥ 0, j = 1, n.
3. Модель задачи ЛП в матричном виде:
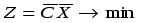
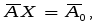 X ≥ 0
X ≥ 0
Где 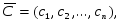
а11 а12 … а1n X1 a1
A= a21 a22 … a2n , X= X2 , A0 = a2
… … … … … …
am1 am2 … amn X3 am
4. Модель задачи ЛП в векторном виде:
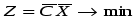
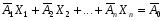
X ≥ 0
Где 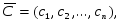
Х1 a11 a12 a1n a1
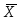 Х2 ,
Х2 , 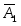 a21 ,
a21 , 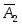 a22 ,
a22 , 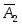 a2n ,
a2n , 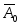 a2
a2
… … … … …
Хn am1 am2 am2 am
15. Переход от стандартной и общей формы задач ЛП к канонической. Теорема связи
Для перехода от общей или стандартной формы к канонической используют следующие приёмы.
1. Преобразование переменных. Если какая-то переменная Xk неположительна (Xk ≤ 0), то вводят новую переменную Xk ', так что Xk ' = –Xk . Очевидно, что Xk ' ≥ 0. После этого в каждом ограничении и целевой функции переменную Xk заменяют на [ – Xk '].
Если какая-то переменная Хt может принимать любые значения, то её заменяют разностью двух неотрицательных переменных Хt’ и Хt’’, т. е. полагают, что хt = Хt’ – Хt’’, где Хt’ 0 ≥ и Хt’’ ≥ 0.
2. Преобразование ограничений. Если какое–либо из ограничений в модели имеет вид неравенства, то оно преобразуется в равенство прибавлением (если неравенство имеет тип ≤) или вычитанием (если неравенство имеет тип ≥) из его левой части. Эти переменные называют балансовыми. Балансовые переменные входят в целевую функцию с коэффициентами нуль. Балансовая переменная принимает значение индекса последовательно после уже имеющихся. Если, например, система ограничений имеет 5 переменных, то первая балансовая переменная будет Х6, а вторая – Х7 и т.д.
Переход от канонической формы модели ЗЛП к стандартной
Для перехода от канонической формы к стандартной можно каждое из
уравнений заменить системой неравенств:
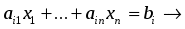
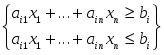
Другой способ состоит в приведении системы уравнений к специальному виду и дальнейшему исключению некоторых переменных.
С помощью метода Жордана-Гаусса выделяем в каждом уравнении базисную переменную. Такое выделение осуществляется с помощью эквивалентных (элементарных) гаусовских преобразований. К ним относятся:
а) умножение любого уравнения на константу отличную от нуля;
б) прибавление к любому уравнению любого другого уравнения, умноженного на любую константу.
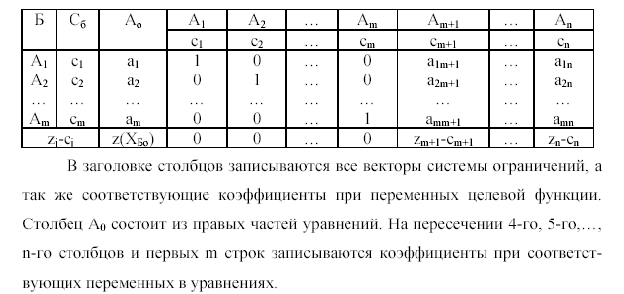
Исходную систему линейных уравнений перед преобразованием удобно записывать в виде матрицы или таблицы:
Далее находим х1, х2 … хn . Далее подставляем в целевую функцию z выражениех1 и х2 … хn.
Записываем задачу в стандартной форме.
17. Понятие гиперплоскости полуплоскости, опорная гиперплоскость.
18. Геометрич. интерпретация системы ограничений и целевой функции в задачи ЛП
19. Выпуклое множество: крайние (угловые) точки множества. Выпуклый многогранник
Определение Множество М называется выпуклым, если вместе с любыми двумя точками, принадлежащими данному множеству, оно содержит и отрезок их соединяющий.
Выпуклое множество
Определение Точка х множества М называется угловой или крайней, если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.
Теорема 1. Любую точку отрезка можно представить в виде выпуклой комбинации его угловых точек.
х = λ1 А + λ2 В
λ1, λ2 ≥ 0 выпуклая комбинация точек угловых точек А и В
λ1 + λ2 = 1
Теорема 2. Любую точку выпуклого замкнутого множества можно представить в виде выпуклой комбинации его угловых точек.
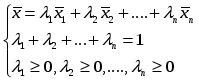
20. алгоритм графического метода решения задач ЛП
Алгоритм графического метода.
1. Проверяется, находится ли исходная ЗЛП в стандартной форме, если нет, то задачу необходимо преобразовать к стандартной форме.
2. Проверяется количество неизвестных переменных. Если это количество больше трёх, то задача не может быть решена графическим методом (существуют другие эффективные методы решения таких задач).
3. Строится область допустимых значений переменных для ЗЛП.
4. Строится направляющий вектор c .
5. Через ОДЗ проводится исходная изоцель (перпендикулярно направляющему вектору).
6. Проводится мысленное перемещение исходной изоцели в направлении вектора c , если определяется максимальное значение целевой функции, или в противоположном направлении, если определяется её минимальное значение, до тех пор, пока изоцель не станет опорной к ОДЗ. Точки пересечения опорной изоцели и ОДЗ и будут оптимальными точками задачи.
7. Для того, чтобы определить координаты оптимальной точки, необходимо решить систему соответствующих линейных уравнений.
8. Для нахождения оптимального значения целевой функции необходимо оптимальные значения переменных подставить в целевую функцию и вычислить её значение.
20. алгоритм графич. метода решения задач ЛП
Алгоритм графического метода.
Последовательным построением каждого из условий системы ограничений задачи осуществляется построение ОДЗ.
Строится направляющий вектор С по коэффициентам при переменных целевой функции.
Перпендикулярно направляющему вектору через начало координат проводится исходная изоцель.
Проводится мысленное перемещение исходной изоцели в направлении возрастания значений вектора С, если определяется максимальное значение целевой функции или в противоположном направлении, если определяется ее минимальное значение, до тех пор, пока изоцель не станет опорной к ОДЗ. Точки пересечения опорной изоцели и ОДЗ будут оптимальными точками задачи.
Для определения координат оптимальной точки необходимо решить систему соответствующих линейных уравнений тех условий, на пересечении которых находится оптимальная точка.
Для нахождения оптимального значения целевой функции, необходимо координаты оптимальной точки подставить в целевую функцию и вычислиь ее значение.
23. теоремы об области допустимых значений задачи ЛП и о целевой ф-ции
Теорема об ОДЗ. Область допустимых решений задачи ЛП выпуклое множество (замкнутое и ограниченное в n-мерном пространстве)
Теорема 2. О целевой функции задачи линейного программирования.
Целевая функция ЗЛП принимает своё оптимальное значение в одной из угловых точек области допустимых значений переменных. Если целевая функция принимает своё оптимальное значение в нескольких угловых точках, то такое же значение она принимает и в любой точке, являющейся выпуклой комбинацией данных угловых точек.
24. Теорема об угловой точке. Достаточное и необходимое условие
25. Следствия из теоремы о свойствах решений задач ЛП и выводы. Понятие опорного плана.
Следствия из теорем.
Определение. План 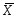 = (х1,х2,…,хn), положительным координатам которого соответствуют линейно независимые векторы, называется опорным планом ЗЛП.
= (х1,х2,…,хn), положительным координатам которого соответствуют линейно независимые векторы, называется опорным планом ЗЛП.
Следствие1. Опорный план имеет не более m положительных координат.
Если он имеет ровно m положительных координат, то такой опорный план называется невырожденным, в противном случае вырожденным.
Следствие 2. Каждая угловая точка ОДЗ является опорным планом.
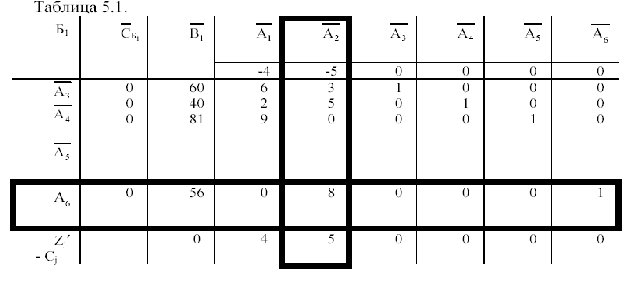
27. Алгоритм симплексного метода.
При решении задач ЛП симплексным методом необходимо выполнить следующую последовательность действий.
Проверяется, находится ли задача ЛП в канонической форме. Если нет, то необходимо исходную модель преобразовать в каноническую форму.
Выделяется начальный опорный план и значение целевой функции при этом опорном плане.
Проводится построение исходной симплексной таблицы.
Проверяются значения оценок оптимальности в индексной строке. Если нет положительных оценок, то выписывается оптимальное решение и алгоритм заканчивает свою работу. В противном случае выполняется пункт 5.
В базисе вводится вектор, которому соответствует наибольшая положительная оценка. Данный столбец называется разрешающим.
Из базиса выводится вектор, которому соответствует симплексное отношение, рассчитанное по формуле 0 < Ө ≤
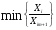 . Данная строка называется разрешающей строкой.
. Данная строка называется разрешающей строкой.Строится новая симплексная таблица. Соответствующим образом изменяются столбцы Б и СБ. остальная часть таблицы заполняется из предыдущей с помощью гауссовских преобразований, причем индексная строка считается m+1 строкой и также преобразуется с помощью гауссовских преобразований. Переходим к выполнению пункта 4 данного алгоритма.
После построения каждой таблицы можно проверить правильность вычислений с использованием формул вычисления оценок, приведенных в предыдущем параграфе.
28. выбор базиса и построение начального опорного плана при решении задач симплекс методом.
29. Симплекс-таблицы, их заполнение. Формулы расчета коэффициентов индексной строки.
30. Теорема оптимальности плана задачи линейного программирования следствие из теоремы оценки оптимальности при решении задач симплекс методом.
Теорема 1: Если для некоторого вектора Āj в системе
Х1 + а1m+1Xm+1 + а1m+2Xm+2 + … + а1nXn = a1
Х2 + а2m+1Xm+1 + а2m+2Xm+2 + … + а2nXn = a2
…………………………………………………..
Xm + аmn+1Xm+1 + аmn+2Xm+2 + … + аmnXn = am
Выполняется соотношение Zj – cj > 0, то план ХБ0 не является оптимальным и можно перейти к плану ХБ1 такому, что Z (ХБ1) ≤ Z (ХБ0).
Здесь Zj = (С, Āj) – скалярное произведение векторов.
С – вектор, состоящий из коэффициентов при базисных переменных целевой функции Z
Āj – вектор, состоящий из коэффициентов разложения соответствующего вектора по векторам базиса.
cj – коэффициент целевой функции Z при переменной Хj
Следствие из теоремы: Если для всех векторов Ā1, Ā2, …, Ān некоторого опорного плана Х выполняется соотношение Zj – cj < 0, то опорный план Х является оптимальным. Величины (Zj – cj) – называются оценками оптимальности соответствующих векторов.
Таким образом теорема и следствие позволяют установить, является ли очередной опорный план оптимальным и, если не является, то необходимо перейти к другому опорному плану, при котором значение целевой функции будет меньше.
Замечание. В теореме и следствии предполагается, что задача находится в канонической форме с целевой функцией на минимум. Однако симплекс-методом моно решать и задачи с целевой функцией на максимум. В этом случае при анализе значений оценок используется их противоположный смысл, то есть план будет оптимальным, если все оценки оптимальности будут не отрицательными (положительным или отрицательным).
31. Выбор вектора, вводящегося в базис и выводящегося из базиса. Симплексное отношение.
Для перехода к новому опорному плану необходимо один из свободных векторов 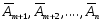 ввести в базис, а какой-то из базисных векторов вывести. Для введения в базис выберем вектор, имеющий хотя бы одну положительную координату. Пусть таким вектором будет вектор А m+1 .
ввести в базис, а какой-то из базисных векторов вывести. Для введения в базис выберем вектор, имеющий хотя бы одну положительную координату. Пусть таким вектором будет вектор А m+1 .
Разложению –
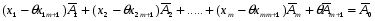 соотв. вектор, кот. будет являться опорным планом, если его координаты будут неотрицательными, а кол-во положительных координат будет равняться m.
соотв. вектор, кот. будет являться опорным планом, если его координаты будут неотрицательными, а кол-во положительных координат будет равняться m.
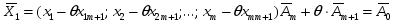
Координаты вектора Х1 должны быть неотрицательными, т.е. 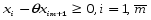 .
.
Если 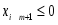 , то эта координата будет неотрицательной.
, то эта координата будет неотрицательной.
Пусть минимум в соотношении (5) был получен при i =1, тогда если взять
то первая координата вектора 1 х станет равной нулю.
Соотношение (6) называется симплексным отношением. Таким образом, мы перешли от исходного опорного плана 0 х (базисные векторы А1,А2,…Аm) к опорному плану 1 х (базисные векторы А2,А3,…,Аm,Am+1).
32. разрешающий элемент таблицы, его выбор. Правило полных жордановых исключений для перерасчета симплекс таблицы.
33. Правило «четырехугольника» для перерасчета симплекс-таблицы
34. Признак единственности оптимального плана, множества оптимальных планов и отсутствия оптимального плана при решении задача ЛП симплекс-методом.
При решении задач симплекс-методом возможны следующие виды оптимальных решений:
1. Единственность. Если оценки всех свободных векторов строго отрицательные, то полученный опорный план является оптимальным и единственным. (см. пример в предыдущем параграфе).
2. Альтернативный оптимум (множество оптимальных решений).
Если среди неположительных оценок свободных векторов имеется хотя бы одна нулевая, то полученный опорный план будет оптимальным, но не единственным. В этом случае можно перейти к другим опорным планам (вводятся в базис векторы, которым соответствуют нулевые оценки) и, затем, общее оптимальное решение записать в виде выпуклой комбинации полученных оптимальных опорных планов.
3. ЗЛП не имеет оптимального решения, так как целевая функция не ограничена снизу. Если в симплекс таблице имеется положительная оценка, а все элементы данного столбца отрицательны и нулевые, то данный вектор можно ввести в базис. Однако никакой из базисных векторов нельзя вывести из базиса. Из этого следует, что дальнейшее уменьшение целевой функции возможно при переходе к неопорному плану.
4. ЗЛП не имеет оптимального решения, так как система ограничений противоречива. Поскольку при решении ЗЛП обычным симплекс-методом должен быть исходный опорный план, то система линейных уравнений заведомо не противоречива. Следовательно, такой случай не может встретиться при решении обычным симплекс методом.
5. Если ОДЗ состоит из одной точки, то решение такой задачи является тривиальным, и может быть получено без использования симплекс-метода.
35. В каких случая применяется метод искусственного базиса
Если задача линейного программирования находится в канонической форме, однако, не во всех уравнениях присутствуют базисные переменные, т. е. исходный опорный план отсутствует. В этом случае в те уравнения, в которых нет базисных переменных, необходимо добавить с коэффициентом +1 некоторую неотрицательную переменную. Такая переменная называется искусственной.
36. Построение М-задачи в методе искусственного базиса
Если задача линейного программирования находится в канонической форме, однако, не во всех уравнениях присутствуют базисные переменные, т. е. исходный опорный план отсутствует. В этом случае в те уравнения, в которых нет базисных переменных, необходимо добавить с коэффициентом +1 некоторую неотрицательную переменную. Такая переменная называется искусственной.
Искусственную переменную необходимо добавить в целевую функцию с очень большим положительным числом (так как целевая функция на нахождения минимума). Это число обозначается латинской буквой M. Его можно считать равным +∞. В связи с этим иногда метод искусственного базиса называют М- методом. Такое преобразование исходной задачи называется построением расширенной задачи. Если решается задача с целевой функцией на нахождение искусственную переменную необходимо добавить в целевую функцию с очень большим положительным числом (так как целевая функция на нахождения минимума). Это число обозначается латинской буквой M. Его можно считать равным +∞. В связи с этим иногда метод искусственного базиса называют М- методом. Такое преобразование исходной задачи называется построением расширенной задачи. Если решается задача с целевой функцией на нахождение максимума, то искусственные переменные входят в целевую функцию с коэффициентом –М.
Таким образом, в расширенной задаче мы имеем опорный план (хотя некоторые из базисных переменных и являются искусственными).
Строится исходная симплекс таблица.
37. построение индексной строки в методе искусственного базиса
Строится исходная симплекс таблица, в которой индексная строка разбивается на две строки, поскольку оценки состоят из двух слагаемых. В верхней строке записывается слагаемое оценки без M, в нижней строке – коэффициенты при М. Знак оценки определяется знаком коэффициента при M, независимо от величины и знака слагаемого без M, так как M очень большое положительное число.
Таким образом, для определения вектора, который вводится в базис необходимо провести анализ нижней индексной строки. Если выводится из базиса искусственный вектор, то соответствующий столбец в последующих симплексных таблицах можно не вычислять, если нет необходимости в получении решения двойственной задачи (см. следующую тему).
После того, как все искусственные векторы будут выведены из базиса, нижняя строка будет иметь все нулевые элементы, за исключением оценок, соответствующих искусственным векторам. Они будут равны –1. Такую строку можно удалить из рассмотрения и дальнейшее решение проводить обычным симплекс-методом, если нет необходимости в получении решения двойственной задачи (см. следующую тему).
38. Критерий оптимальности в методе искусственного базиса. Признак построение начального опорного плана исходной задачи.
39. Алгоритм двойственного симплекс-метода
Алгоритм двойственного симплекс-метода:
обычным способом заполняют первую симплекс-таблицу не обращая внимания на знаки свободных членов. Считается, что такая задача должна иметь исходный единичный базис.
Выбирают направляющую строку по наибольшему по абсолютной величине отрицательному элементу столбца свободных членов А0
Выбирают направляющий столбец по наименьшему по абсолютной величине отношению элементов индексной строки к отрицательным элементам направляющей строки.
Пересчитывают симплексную таблицу по правилу полных жордановых исключений
проверяют полученный план на допустимость. Признаком получения допустимого опорного плана является отсутствие в столбце А0 отрицательных элементов. Если в столбце А0 имеются отрицательные элементы то переходят ко второму пункту. Если же их нет, то переходят к решению полученной задачи обычным способом.
признаком получения оптимального решения двойственным симплекс-методом является критерий оптимальности обычного симплекс-метода.
41. Открытые и закрытые транспортные модели. Переход от открытой транспортной модели к закрытой.
Типы транспортных задач.
Имеются m поставщиков однородной продукции с известными запасами продукции и n потребителей этой продукции с заданными объёмами потребностей. Известны так же удельные затраты на перевозку.
Если сумма объёмов запасов продукции равна объёму потребностей всех потребителей, то такая задача называется закрытой транспортной задачей
(т. е. если ∑ Ai = ∑ Bj), в противном случае транспортная задача называется открытой. Для решения транспортной задачи необходимо, чтобы она была закрытой.
Открытую транспортную задачу можно преобразовать к закрытой следующим образом.
Пусть ∑Ai > ∑Bj. В этом случае необходимо ввести фиктивного n+1 потребителя с объёмом потребностей ∑Ai – ∑Bj Удельные затраты на перевозку от поставщиков к фиктивному потребителю полагаются равными 0, так как на самом деле такие перевозки осуществляться не будут и некоторая часть продукции останется у поставщиков.
Если ∑Bj > ∑Ai . В этом случае необходимо ввести фиктивного m+1 поставщика с объёмом запасов∑Bj – ∑Ai . Удельные затраты на перевозку от фиктивного поставщика к потребителям полагаются равными 0, так как на самом деле такие перевозки осуществляться не будут и некоторую часть продукции потребители недополучат.
42. Способы построения первоначального распределения в транспортной задаче: метод северо-западного угла и метод наименьшего элемента в матрице.
Северо-западный прием построения опорного плана. Согласно этому приему формирование величин перевозок начинается с с.-з. уголка таблицы, т.е. с клетки x11. По этому приему прежде всего распределяется товар первого поставщика. Причем первый поставщик сначала предельно возможно удовлетворяет первого потребителя. Затем, если у поставщика товар еще остался,
Метод наименьшего элемента в матрице.
Сущность метода заключается в том, что максимально возможная поставка всегда проставляется в клетку, которой соответствует наименьший тариф матрицы.
Сначала делаем пометки (например, знаком ▼ ) в тех клетках строк, в которых наблюдается самая меньшая цена по строке. Затем обходим таблицу по столбикам и делаем такие же пометки в клетках, в которых самая маленькая цена по столбикам.
Дальнейшее распределение делается сначала предельно возможно по клеткам с двумя отметками, потом - с одной, а затем делается добалансировка задачи до (m + n – 1) заполнений. Заполнения организуем при прохождении таблицы слева направо и сверху вниз.
43. Свойства транспортных задач
Транспортная задача обладает некоторыми свойствами, которые можно отразить следующими теоремами.
Теорема 1. Закрытая транспортная задача всегда имеет решение.
Теорема 2. Если объёмы запасов продукции и объёмы потребностей является целыми числами, то и решение транспортной задачи также будет целочисленным.
Теорема 3. система ограничений закрытой транспортной задачи всегда линейно-зависима.
Из этой теоремы следует, что распределение закрытой транспортной задачи всегда имеет m + n – 1 базисную переменную и (m – 1) (n – 1) свободные временные.
44. Вырожденное распределение в транспортных задачах, избавление от вырожденности. Вычеркиваемая комбинация.
Распределение называется вырожденным, если количество клеток меньше чем m + n – 1.
45. Теорем оптимальности транспортной задачи.
Теорема. Если для некоторого распределения транспортной задачи вы-
полняются условия:
а). ui+vj = сij для занятых клеток
б) ui+vj ≤ сij,, для свободных клеток,
то данное распределение является оптимальным.
Величины ui называют потенциалами строк, а величины vj называют потенциалами столбцов.
46. Потенциалы и способы их расчета.
Для нахождения потенциалов строк и столбцов пользуются следующими рассуждениями, исходя из условия а) теоремы оптимальности.
Количество уравнений исходя из этого условия равняется m + n – 1, а количество неизвестных ui и vj равняется m + n. Т.о. количество переменных больше количества уравнений, причем все уравнения линейно независимы. Решение такой системы линейных уравнений является неопределенным, поэтому одному из потенциалов нужно присвоить любое значение. На практике ui = 0. получается система из m + n – 1 уравнений с m + n – 1 неизвестными переменными. Эту систему можно решить любым методом. На практике для расчета потенциалов рассматриваются занятые клетки, для которых один их потенциалов известен, и исходя из условия а) теоремы вычисляются значения остальных неизвестных потенциалов.
47. расчет оценок оптимальности распределения транспортных задач и критерий оптимальности.
Исходя из соотношения б) теоремы можно записать следующую формулу для вычисления оценок: δ ij = ui +vj – сij. Для того, чтобы оценки не перепутать с объёмами перевозок, они (оценки) заключаются в круги.
Оценки оптимальности в свободных клетках ТЗ представляют собой критерий оптимальности, с помощью которого осуществляется проверка распределения на оптимальность. Если оценки всех свободных клеток меньше или равны нулю, то данное распределение является оптимальным.
48. перераспределение поставок в транспортной задаче
Если распределение не является оптимальным, то необходимо осуществить перераспределение поставок.
Для перераспределения осуществляют построение цикла пересчета. В качестве клетки выбирается клетка с наибольшей положительной оценкой. Эта клетка помечается знаком «+», то есть в неё необходимо записать некоторый объём поставки. Но тогда нарушится баланс по данному столбцу, следовательно, одну из занятых клеток данного столбца необходимо пометить знаком «-», то есть уменьшить объём поставки на такую же величину. Но тогда изменится баланс по данной строке, следовательно, какую-то занятую клетку данной строки необходимо пометить знаком «+». Данный процесс продолжается до тех пор, пока не поставлен знак «-» в строке, где находилась исходная клетка.
Для любой свободной клетки существует цикл пересчета и притом единственный.
49. цепочки перераспределения, их виды.
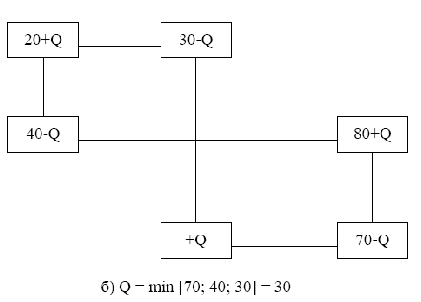
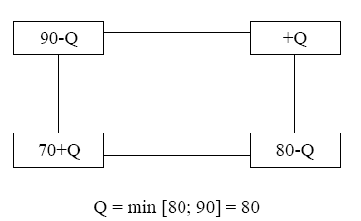
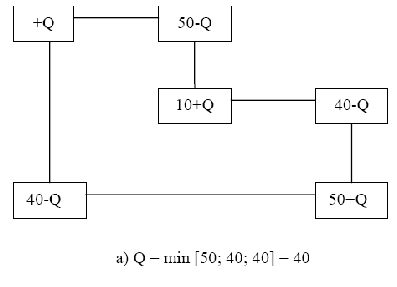
Пусть рассматриваемый план перевозок не оптимальный, т.е. имеются положительные относительные оценки. Тогда берется неблагоприятная клетка (одна из неблагоприятных) и для нее строится цикл пересчета, согласно которому потом делается перераспределение намеченных перевозок. Цикл строится в виде ломаной замкнутой линии, отрезки которой идут либо вдоль столбика, либо вдоль строки. В одном из углов ломаной претендующая на товар неблагоприятная клетка, а в остальных углах клетки заполненные, т.е. при построении цикла мы исходим из претендующей клетки и возвращаемся в нее по ломаной, но повороты мы можем делать только в клетках заполненных (соответствующих базисным переменным). Пусть неблагоприятная клетка претендует на товар Q. Чтобы не произошел разбаланс в таблице, надо в переходах по циклу по очереди
прибавлять и отнимать Q к имеющимся перевозкам. Так как углов чётное количество, в половине клеток Q прибавится, а в другой половине - отнимется. Обход цикла начинают по часовой стрелке или против с претендующей клетки, помещая туда товар Q, затем из соседней клетки вычитают Q, затем прибавляют и т.д. Сама величина Q выбирается так, чтобы одна из клеток опустошалась, но ни одна из поставок не стала бы отрицательной.
Для этого Q надо выбрать равным наименьшему уменьшаемому из клеток, в которых Q вычитается. На следующих рис. 7.1 и 7.2 покажем примеры циклов и правило вычисления.
При этом опустошаются две клетки. Но надо, чтобы взаимно пустой стала лишь одна клетка. Поступают так: одну из опустошающихся клеток делают пустой в новой таблице, а в другой опустошающейся клетке ставят нуль. Эта клетка считается в новой таблице базисной (заполненной).
50. Выбор объема перераспределения.
Определение объёма перемещаемой продукции. При определении объёма продукции, перемещаемого по циклу пересчёта, мы должны исходить из следующих двух соображений:
а) после преобразования в клетках таблицы не должны получиться отрицательные числа;
б) одна из занятых клеток должна стать свободной.
Для того, чтобы эти условия выполнялись, необходимо объём перемещаемой продукции выбрать следующим: θ=min {хij} -, где {хij} – объёмы перевозок из клеток цикла пересчёта, помеченных знаком «-».
θ = min{20;30}=20
К значениям клеток, помеченных знаком «+»прибавляется θ. От значений клеток, помеченных знаком «-», вычитается θ. Значение поставок остальных клеток переписывается без изменений. В результате получим следующую таблицу.
53. Алгоритм метода потенциалов.
Алгоритм:
1. Проверить, выполняется ли для задачи рав-во 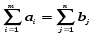 если нет, то в задачу вводится фиктивный поставщик или потребитель
если нет, то в задачу вводится фиктивный поставщик или потребитель
2. Условие задачи записывается в форме транспорт.таблицы
3. Строится начальный опорный план
4. Определяются потенциалы пост-ков и потреб-лей
5. Вычисляются оценки свободных клеток. Если все они не отрицательные – план оптимальный и нужно выписать ответ. Матрицу перевозок Х и определить величину затрат на транспортировку. Если план не явл-ся оптимальным, т.е.среди оценок есть отриц-ые, то выбир-т перспективную клетку с наибольшей по величине отриц. оценкой и переходят по величине к след.
6. Загруж-т перспективную клетку. Оформл-т нов.опорн.план в виде трансп.таблицы. Переходят к пункту 4.
54. Учет затрат на производство и транспортировку продукции. Транспортная задача с запретами на поставки.
При решении некоторых задач необходимо учитывать затраты не только на перевозку груза, но и на производство перевозимой продукции. Для этого в матрице трансп. задачи
Где Cij ‘ – приведенные затрат на производство одной единицы продукции.
Cij “– затраты на транспортировку одной единицы продукции.
Дальше задача решается обычным способом.
Задачи с запретами на поставки.
В некоторых ситуациях нельзя перевозить продукцию по какому-либо маршруту.
Для этого в матрице транспортной задачи перевозка через которую является запретной проставляется запрещающий тариф М. дальше задача решается обычным способом., однако этой клетке всегда будет соответствовать отрицательная оценка клетки.
55. учет ограничений по пропускной способности маршрутов, учет обязательности некоторых поставок в транспортной задаче.
учет ограничений по пропускной способности маршрутов.
В некоторых транспортных задачах по некоторым маршрутам устанавливают меньшую пропускную способность чем необходимо для удовлетворения спроса пункта потребления.
учет обязательности некоторых поставок в транспортной задаче.
В некоторых случаях в задаче требуется, что например по маршруту Ak Bs должно обязательно осуществиться поставка в объема А ед. В этом случае из объема производства пункта А и объем S Bs вчитается обязательная поставка и задача решается относительно необязательности поставок. После получения оптимального решения обязательно поставка добавляется к объему стоящему в клетке Ak Bs.
56. Возможные выводы при экономич. интерпретации оптимального распределения для открытых транспортных задач.
При получении оптимального распределения необходимо вернуться к исходной задаче и сделать соответствующие экономич. выводы. Они следующие:
если введен пункт потребления, то это означает, что в анализируемоой системе излишни объемы производства, и можно без ущерба для рассматриваемой системы уменьшить мощности тех пунктов производства на величину привязки, которые привязались к фиктивному пункту потребления.
если же введен фиктивный пункт производства, то это означает, что мощностей реальных пунктов производства не хватает и их необходимо увеличить. Увеличиваются мощности тех пунктов производства, которые ближе всего расположены к пунктам потребления, привязанным к фиктивному пункту производства. Производится увеличение мощности производителя на величину привязки. Для этого рассматривают столбец пункта потребления, который привязан к фиктивному пункту производства, и находят в нем наименьший тариф. Мощность соответствующего этому тарифу пункта производства наиболее эффективно увеличить на величину привязки.
57.Понятие двойственности. Экономическая постановка двойственных задач на примере задачи об оптимизации плана выпуска продукции.
Двойственная задача - это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой задачи.
Пусть имеется зада об оптимизации плана выпуска продукции. Она имеет следующий вид:
Исходная задача:
а11х1+а12х2+…+ а1пхп≤в1 |у1
а21х1+а22х2+…+ а2пхп≤в2 |у2
……………….. |.. (1)
ат1х1+ат2х2+…+ атпхп≤в1 | ут
xj≥0, j = 1,n(2)
z = c1x1+c2x2+…+cnxn ->max(3)
_
X = (x1,x2,…, xn)
aij – кол-во сырья i- го вида, затраченного для выпуска j-го вида продукции
Двойственная задача
Пусть предприятие по какой-либо причине не может выпускать продукцию. Для того, чтобы уменьшить затраты простоя, предприятие может реализовать сырье, которое у него имеется. По каким ценам нужно реализовать сырье?
уi- цена i- го вида сырья имеющегося на предприятии.
а11у1+а21у2+…+ ат1ут≥с1
а12х1+а22у2+…+ ат2хп≥с2
……………….. (1’)
а1пу1+а2пу2+…+ атпут≥сп
уi≥0, j = 1,m(2’)
F = b1y1+b2y2+…+bmym ->min(3’)
58. Соответствие между структурными элементами прямой и двойственной задачи
Каждой задаче линейного программирования можно сопоставить
двойственную задачу по следующим правилам:
1. Во всех ограничениях исходной задачи свободные члены должны
находиться справа, а члены с неизвестными - слева.
2. Ограничения-неравенства исходной задачи должны иметь знаки,
направленные в одну строну.
3. Если целевая функция в исходной задаче минимизируется, ограничения-неравенства следует записать со знаком «≤» , тогда в двойственной задаче целевая функция будет минимизироваться и знаки ограничений-неравенств будут «≥».
4. Каждому ограничению исходной задачи соответствует переменная в
двойственной задаче. Если переменная соответствует неравенству, она неотрицательна, если равенству – то переменная без ограничений на знак («произвольная»).
5. Коэффициенты при переменных в ограничениях двойственной задачи получаются транспонированием матрицы, составленной из
коэффициентов при переменных исходной задачи.
6. Свободные члены исходной задачи являются коэффициентами при
переменных в функции цели двойственной задачи, а свободными
членами в двойственной задаче – коэффициенты при переменных в
функции исходной задачи.Отметим также, что соотношение двойственности взаимное, т.е. задача, двойственная по отношению к двойственной, совпадает с исходной.Двойственные пары задач подразделяются на симметричные и несимметричные. В симметричной паре ограничения прямой и двойственной задач являются нестрогими неравенствами и, следовательно, переменные обеих задач могут принимать только неотрицательные значения.
59. Построение двойственных задач к исходным задачам, записанным в стандартной, канонической и общей форме модели(построение симметричных и несимметричных двойств. задач)
Стандартная форма (исходная)
n
Σ aijxj ≤ bi, i=1,n(1)
j=1
xj≥0, j=1,n(2)
n
z = Σ cjxj ->max(3)
j=1
Двойственная стандартная
m
Σ aijyi ≤ cj, j=1,n(1)
i=1
yi≥0, j=1,m(2)
m
F = Σ biyi ->min(3)
i=1
Исходная задача в канонической форме:
n
Σ aijxj = bi, i=1,m(1)
j=1
xj≥0, j=1,n(2)
n
z = Σ cjxj ->min(3)
j=1
Двойственная каноническая
m
Σ aijyi ≤ cj, j=1,n(1)
i=1
yi- любые (2)
m
F = Σ biyi ->max(3)
i=1
Дадим экономическую интерпретацию пары двойственных задач. Рассмотрим задачу рационального использования ресурсов. Пусть предприятие располагает ресурсами b1,b2,…bm, которые могут использ-ся для выпуска n-видов продукции. Пусть также известны стоимость единицы j-вида продукции cj (j=1,n) и норма потребления i-го ресурса (i=1,m) на производство единицы j-й продукции – aij.Требуется определить объем производства продукции каждого вида xj (j=1,n), максимизирующий суммарную стоимость
f= c1x1+…+cnxn (1)
При этом расход ресурсов не должен превышать их наличия:
a11x1+…+a1nxn<=b1 }
…………………….. } (2)
am1x1+…+amnxn<=bm }
Все известные по своему экономическому смыслу неотрицательны:
Xj>=0 (j=1,n). (3)
Заметим, что это задача образуют симитричную двойственную задачу.
Несимметричные двойственные задачи.
Возьмем ЗЛП на максимум в канонической форме:
Max Z=(n;j=1)Σcj*xj
(n;j=1)Σaij*xj=bi (i=1,m)
Xj>=0 (j=1,n).
60.Основная и вторая теорема двойственности (сформулировать теоремы и разъяснить)
Первая теорема двойственности.
Теорема: если одна из двойственных задач имеет оптимальный план, то и другая решима, т.е. имеет опт.план. При этом экстремальные значен.целевых функций совпадают (j=от 1 до n) Σcjxj*= (i=от 1 до m)Σbiyi* если в исходн. задаче целевая функция неограниченна на множестве планов, то в двойственной задаче система ограничений несовместна.
Вторая теорема двойственности и ее эконом.интерпритация.
Для того, чтобы допустимые решения пары двойственных задач были оптимальными, необходимо и достаточно выполнение условия: xj*(∑aij yi*-cj)=0, j от 1 до n, yi*(∑aij xj*-bi)=0, I от 1 до m. Это условия дополняющей нежесткости. Из них следует: если какое-либо ограничение двойств.задачи обращ-ся оптималь.планом в строгое равенство, то соответствующая компонента опт. плана двойственной задачи должно равняться нулю.Если же какая-то компонента опт. плана равна нулю, то соответствующее ограничение двойств.задачи обращается опт.планом в строгое равенство хj*>0 следовательно (i= от 1 до m)Σaij yi*=cj (затраты на пр-во продукции=цене) – Если продукция вошла в опт.план, то если затраты>цены, объем пр-ва=0 Σaij yi* >cj следовательно xj*=0
yi*>0 следовательно (j=от 1 до n) Σaij xj*=bi (рас-ды рес-ов =запас рес-ов).
(j=от 1 до n) Σaij xj*
Смысл теоремы сводится к следующему:
-если стоимост.оценка рес-ов расход-х на пр-во ед.прод-ии=цене, то этот вид прод-ии входит в оптим.план ;
-если затраты превышают цену, то прод-ию производить не следует;
- еслирасход рес-ов=запасу, то стоимост.оценка этого рес-са положительна. Такой рес-с наз-ся дефицитным. Наибелее дефицит.рес-с обладает наибольшей оценкой;
-если рес-с израсходован неполностью, то его стоимост.оценка = 0.
61. Построение оптимального опорного плана двойственной задачи по симплексной таблице исходной задачи
Информация из столбцов обратной матрицы линейных преобразований, приведших к оптимальному результату. Из столбцов матрицы D-1 можно почерпнуть весьма полезную информацию.
Столбец A3: «теневая» цена ресурса S2 равна y01=0, столбец остался
единичным и по первой строке можно прочесть, что x3=9, т.е. при реализации найденного оптимального плана 1-й ресурс окажется в избытке, причем этот избыток (недоиспользование) как раз составит 9 условных единиц.
Столбец A4: «теневая» цена ресурса S2 равна y02=1, ресурс будет полностью использован и его возможное увеличение будет вести к увеличению целевой функции (т.е. дохода). И т.к. y02=1, то увеличение ресурса S2 на 1 у.е. будет давать добавку по доходу на .Z = y02· .в2 = = 1.1 = 1 (тыс. грн.) (здесь .в2 -приращение ресурса S2 и .Z - соответствующее приращение дохода ). При таком приращении ресурса S2 максимальный доход уже составит Zmax=58 тыс. грн. + 1 тыс. грн = 59 тыс. грн. На рис. 6.2 проиллюстрирована эта ситуация, комментарий по отношению к которой будет приведен ниже. Из столбца A4 еще следует, что при увеличении ресурса S2 на 1 у.е. для новой оптимальной точки выпуск товара T1 сократится на ½ тонны (на пересечении строки базисной переменной x1 и столбца A4 стоит «-1/2»), а выпуск товара T2 увеличится на 3/2 тонны (т.к. в строке с базисной переменной x2 в столбце A4 имеем «3/2»).Сказанное по столбцу A4 будет ниже прокомментировано с помощьюграфических построений (рис. 6.2).Столбец A5: «теневая» цена ресурса S3 равна y03=2. Это означает, чтоувеличение ресурса S3 на 1 у.е. принесет добавку по Z на .Z = y03· .в3 = 2.1 =2(тыс. грн.) и составит Zmax=58 тыс. грн. + 2 тыс. грн = 60 тыс. грн. При этом, как следует из столбика A5 табл. 3, выпуск T1 увеличится на ½ тонны, а T2 уменьшится на ½ тонны. Запас по сырью S1 (см. 1-ю строку) увеличится на 3/2 у.е.
62. Идея метода динамического програмирования и его геометрическая интерпретация. Принцип оптимальности Беллмана.
Оптимальное решение задачи методом динамического программирования находится на основе функционального уравнения
fn-1(Sl)=optimum(Rl+1(Sl,Ul+1)+fn-(l+1)(Sl+1)) (1)
ul+1
(l=0,n-1)
Чтобы определить его, необходимо:
1.записать функциональное уравнение для последнего состояния процесса (ему соответствует l=n-1)
fn-1(Sl-1)=optimum(Rn(Sn-1,Un)+f0(Sn))
ul+1
2.найти Rn(Sn-1,Un) из дискретного набора его значений при некоторых фиксированных Sn-1 и Un из соответствующих допустимых областей (так как f0(Sn)=0, то f1(Sn-1)= optimum(Rn(Sn-1,Un)
Un
В результате после первого шага известно решение Un и соответствующее значение функции f1(Sn-1)
3.Уменьшить значение l на единицу и записать соответствующее функциональное уравнение. При l=n-k (k= 2,n) оно имеет вид
fk(Sn-k)=optimum(Rn-k+1(Sn-k,Un-k+1)+fk-1(Sn-k+1)) (2)
Un-k+1
4.найти условно-оптимальное решение на основе выражения (2)
5.проверить, чему равно значение l.Если l=0, расчет условно-оптимальных решений закончен, при этом найдено оптимальное решение задачи для первого состояния процесса. Если l не равно 0, перейти к выполнению п.3.
6.Вычислить оптимальное решение задачи для каждого последующего шага процесса, двигаясь от конца расчетов к началу.
Метод динам программ позволяет одну задачу со многими переменными заменить рядом последовательно решаемых задач с меньшим числом переменных. Решение осуществляется по шагам. Основной принцип, на котором базируется оптимизация многошагового процесса, а также особенности вычислительного метода—принцип оптимальности Беллмана.
Оптимальное поведение обладает тем свойством, что каковы бы ни были начальное состояние и начальное решение, последующие решения должны быть оптимальными относительно состояния, полученного в результате первоначального решения.
Математически он записывается выражением вида:
fn-1(Sl)=optimum(Rl+1(Sl,Ul+1)+fn-(l+1)(Sl+1)) (1)
ul+1
(l=0,n-1)Optimum в выражении означает максимум или минимум в зависимости от условия задачи.
63. Требования, предъявляемые к задачам, решаемым методом ДП
Динамическое программирование—математический метод для нахождения оптимальных решений многошаговых задач. Многошаговым является процесс, развивающийся во времени и распадающийся на ряд шагов, или этапов.
Одна из особенностей метода динамического программирования состоит в том, что принятые решения по отношению к многошаговым процессам рассматривается не как единичный акт, а как целый комплекс взаимосвязанных решений. Эту последовательность взаимосвязанных решений называют стратегией.Цель оптимального планирования—выбрать стратегию, обеспечивающую получение наилучшего результата с точки зрения заранее выбранного критерия. Такую стратегию называют оптимальной.
Другой важной особенностью метода является независимость оптимального решения, принимаемого на очередном шаге, от предистории, т.е. от того, каким образом оптимизируемый процесс достиг теперешнего состояния. Оптимальное решение выбирается лишь с учетом факторов, характеризующих процесс в данный момент.
Метод динам программ характеризуется также тем, что выбор оптимального решения на каждом шаге должен производиться с учетом его последствий в будущем. Это означает, что, оптимизируя процесс на каждом отдельном шаге, ни в коем случае нельзя забыть обо всех последующих шагах.
64.Экономическая постановка и построение математической модели задачи, решаемой методом ДП(на примере задачи о распределении капиталовложений). Рекуррентное соотношение Беллмана.
Предварительно поясним, что метод динамического программирования применяется прежде всего к тем задачам, в которых оптимизируемый процесс (или ситуация) разворачивается в пространстве или во времени, или в том и другом.
Пусть сам процесс (ситуация) настолько сложен, что нет возможности его оптимизировать известными методами. Тогда по методу динамического программирования СЛОЖНЫЙ процесс (операция, ситуация) разбивается (членится) на ряд этапов (шагов). Эта разбивка во многих случаях является естественной, но в общем случае привносится искусственно. Например, при рассмотрении какой-либо партии игры в шахматы любой ход каждого из игроков как раз и служит
разбивке всей партии на отдельные шаги (этапы). А в военной операции по преследованию одной ракеты другой весь непрерывный процесс приходится искусственно разбивать на этапы, например, через каждую секунду наблюдения. Метод динамического программирования позволяет оптимизацию всего сложного процесса заменить условной оптимизацией по каждому из этапов
(шагов) с последующим синтезом оптимального управления всем процессом. При этом метод предусматривает, что условная оптимизация на отдельном шаге (этапе) делается в интересах, прежде всего, всей операции.
Все вычисления, дающие возможность найти оптимальное значение эффекта, достигаемого за n шагов, fn(S0), проводятся по формуле (1), которая носит название основного функционального уравнения Беллмана или рекуррентное соотношение. При вычислении очередного значения функции fn-1 используется значение функции fn-(l+1), полученное на предыдущем шаге, и непосредственное значение эффекта Rl+1(Sl,Ul+1), достигаемого в результате выбора решения Ul+1 при заданном состоянии системы Sl. Процесс вычисления значения функции fn-1(l=0,n-1)
Осуществляется при естественном начальном условии f0(Sn)=0, которое означает, что за пределами конечного состояния системы эффект равен нулю.
65. Задача о распределении капитальных вложений (пример).
Для решения задачи об оптимальном распределении капиталовложений мы будем пользоваться функциональным уравнением Беллмана. Сначала с помощью простейшей ситуации проиллюстрируем вывод функционального уравнения Беллмана, а потом на примере докажем, как использовать это уравнение для решения интересующей нас задачи.
Начнем с оптимального распределения выделенных капиталовложений в сумме К между двумя предприятиями. Плановые отделы предприятий на основе своих расчетов сформировали функции дохода q(x) для предприятия П1 и h(x) - для предприятия П2. Функции эти означают, что если первое или второе предприятие получит капиталовложение и размере х, то первым предприятием
будет получен доход q(x), а вторым h(x), причем величина x может принимать непрерывные или известные дискретные значения от 0 до К.
Итак, пусть предприятию П1 выделены капиталовложения в сумме х, тогда предприятию П2 выделяется сумма К - х. В этом случае от первого предприятия будет получен доход q(x), а от второго - h(К - x). Если капиталовложения К были выделены на один плановый период, то общий доход от двух предприятий составит R(K, x) = q(x) + h(K - x). Очевидно, что x и соответственно К - x надо выбирать такими, чтобы R(K, x) приняло свое максимальное значение, которое мы обозначим через F(K):
Эта запись является как бы остовом для более полных записей
функционального уравнения Беллмана. УСЛОЖНИМ нашу задачу, распределив капиталовложения на два плановых периода (два этапа). Пусть изначально решено первому предприятию П1 выделить сумму х, а второму К – х. В целом доход получался бы равным R(K, x) = q(x) +
h(K - x). Если мы будем иметь в виду, что капиталовложения распределяются на 2 периода (2 этапа), то на первом предприятии остаток капиталовложений составит x, где , а на втором - (К - х), где Соответственно доходы за второй период составят q(x) -по первому предприятию и h[(K - x)] - по второму. Оптимизацию по методу динамического программирования, как правило, начинают с концевого этапа. Поэтому начнем со второго этапа, обозначив F1 максимально возможный доход от двух предприятий на втором
этапе. Получим
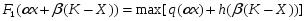
Затем к рассмотренному последнему (в нашем случае второму) этапу как бы пристраиваем предшествующий (у нас первый) этап и находим максимальный доход от двух этапов вместе:
Аналогичным образом для n этапов получаем
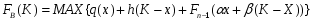
где Fn-1 - целевая функция, дающая наилучший результат за последние (n - 1) этапы. Полученное функциональное уравнение Беллмана носит рекуррентный характер, т.е. связывает значение Fn со значением Fn-1.
В более общем начертании уравнение Беллмана имеет вид
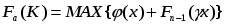
где , Fn-1 - максимальный доход за (n - 1) последних этапов, Fn -
максимальный доход за все n этапов.
66. Понятие о решении задач нелинейного программирования
Пусть задача нелинейного программирования ставится в следующем общем виде: найти такие значения переменных х1, х2,…, хn, которые отвечают условиям:
и приносят требуемый экстремум (максимум или минимум) целевой функции
f = f(х1, х2,…, хn), (13.2)
где f(х1, …, хn) и qi(х1, …, хn) ( m , 1 i ) - действительные нелинейные,
регулярные функции n действительных переменных.
По своим общим свойствам задачи нелинейного программирования могут
существенно отличаться от линейных. Например, область допустимых решений может уже быть невыпуклой, а экстремум целевой функции может наблюдаться в любой точке допустимой области. Существенно отличаются и методы решения нелинейных задач. Рассмотрим лишь некоторые подходы к решению этих задач.
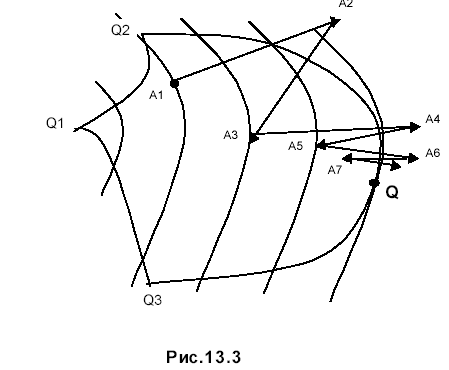
Прежде всего также справедлив графический подход при решении простейших задач нелинейного программирования. Так, если аргументами задачи являются переменные х1 и х2, то сначала на плоскости этих переменных строится область допустимых решений, а затем с помощью уровней целевой функции f(х1,х2) определяется оптимальная точка в области.
В нелинейном программировании для решения многих задач используется градиентный подход. Имеется целый ряд градиентных методов, сущность которых состоит в поиске оптимального результата с помощью градиента целевой функции - вектора, указывающего направление максимального возрастания цели для рассматриваемой точки. В общем случае процедура поиска совершается в итеративном режиме от первоначально выбранной точки к точкам с лучшим показателем. Пусть, например, - о6ласть допустимых решений
рассматриваемой задачи, а итеративный процесс расчетов начинается с точки
Далее, сначала делается переход по градиенту целевой функции, а затем возврат в область по градиенту к нарушенной границе О2 О3 области . На рис. 13.3 показано так, что Ai с нечетными индексами принадлежат области , а точки Аi с четными индексами не принадлежат . По мере приближения к оптимальной точке Q направления рабочих градиентов сближаются. Поэтому идеальным критерием остановки процесса будет коллинеарность градиента цели и градиента нарушенной границы.
67. Понятие о параметрическом и целочисленном программировании.
Постановка и математич модель ЗЦЛП.
В задачах с неделимыми объектами на переменные накладываются условия целочисленности. Иногда эти условия распространяются на все переменные, иногда—на часть переменных.Рассматривают полностью целочисленную задачу
f=(n,j=1)∑CjXi max
(n,j=1)∑AijXj=bi, i=1,m
xj≥0, j=1,n
xi-целое,j=1,n
Теперь в отличие от общей задачи линейного программирования, оптимальный план не обязательно будет в вершине многогранника планов.Существуют следующие методы решения целочисленных задач:
1.Методы отсечения
2.Комбинаторные
3.Приближенные методы..
Параметрическое программирование – раздел математического программирования, посвящённый исследованию задач оптимизации, в которых условия допустимости и целевая функция зависят от некоторых детерминированных параметров.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ