Справочные материалы для учащихся 5 класса по математике "Выражения.Формулы.Уравнения.Задачи"









 ТЕМА 2: ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ. ФОРМУЛЫ. УРАВНЕНИЯ И ЗАДАЧИ, РЕШАЕМЫЕ С ПОМОЩЬЮ УРАВНЕНИЙ. КОМБИНАТОРИКА.
ТЕМА 2: ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ. ФОРМУЛЫ. УРАВНЕНИЯ И ЗАДАЧИ, РЕШАЕМЫЕ С ПОМОЩЬЮ УРАВНЕНИЙ. КОМБИНАТОРИКА.
Раздел 1: Числовые выражения
Запись, составленную из чисел , знаков арифметических действий и скобок , называют числовым выражением
Например: 36:4 – 25; 84 + ( 67 – 37 ) * 4 .
а) Что значит найти значение числового выражения?
Это значит необходимо выполнить все действия над числами, придерживаясь общепринятых правил порядка их выполнения.
Например: ( 327 -123 ) :  + 86 = 137
+ 86 = 137
Порядок выполнения действий: 1) 327-123 = 204; 2)  = 2 * 2 = 4; 3) 204 : 4 = 51 ; 4) 51 + 86 = 137
= 2 * 2 = 4; 3) 204 : 4 = 51 ; 4) 51 + 86 = 137
б) «Чтение» числовых выражений
Числовые выражения необходимо уметь «читать», используя названия действий.
Например: 5+67 – сумма чисел 5 и 67 ; 81 – 9 - разность чисел 81 и 9 ; 2 * ( 5 + 7 ) - произведение 2 и суммы чисел 5 и 7 ;
21 : ( 7 – 4 ) - частное от деления 21 и разности 7 и 4 ;
( 35 + 7 ) * ( 35 – 7 ) – произведение суммы и разности чисел 35 и 7 .
Запомни: Числовое выражение имеет только одно значение ( правильный ответ).
Раздел 2 : Буквенные выражения
Запись, которая состоит из чисел , букв , знаков арифметических действий и скобок , называется буквенным выражением
Например : ( 3 + а ) – 17 ; 6 + 3х ; а : 3 + 5 * к .
В буквенных выражениях используют те же знаки действий ( + , - , * , : ) , как и у числовых ,только часто не пишут знак умножить между числом и буквой. 3* х = 3х .
а) Что значит найти значение буквенного выражения?
Для этого необходимо вместо буквы подставить соответствующее числовое значение и выполнить все действия в полученном числовом выражении :
Пример 1: Найти значение выражения 3х + 5 , если х = 15
Решение: если х = 15 , то 3х + 5 = 3 * 15 + 5 = 45 + 5 = 50
Пример 2 : В первом ящике лежало а яблок , а груши положили в в ящиков по 25 кг. Сколько всего яблок и груш ? Вычислите значение полученного выражения при а = 30 , в = 3 .
Решение : Если груши положили в в ящиков по 25 кг в каждый , то всего груш было 25в ( кг ) . Следовательно, всего яблок и груш было а + 25в ( кг ). Если а = 30 , в + 3 ,то а + 25В = 30 + 25 * 3 = 30 + 75 = 105 ( кг ).
Запомни: Буквенное выражение имеет бесконечно много значений , которые зависят от значений букв .Изменяя значение буквы , мы получаем каждый раз новое значение буквенного выражения.
Раздел 3 : Формулы
Иногда буквенное выражение обозначают одной буквой. Например периметр квадрата обозначили буквой Р. Тогда пишут Р = 4а .Эту запись называют формулой вычисления периметра квадрата.
Известные нам формулы:
№п/п
Название формулы
Формула
1
Периметр квадрата
Р = 4а
2
Площадь квадрата
S = а*а = 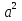
3
Периметр прямоугольника
Р = ( а + в ) * 2
4
Площадь прямоугольника
S = а*в
5
Нахождение расстояния ( пути ), S - расстояние
S = v * t
6
Нахождение скорости , v - скорость
V = S : t
7
Нахождение времени , t - время
t = S : v
8
Нахождение объёма куба
9
Нахождение площади поверхности куба
10
Нахождение суммы длин всех ребер куба
11
Нахождение объёма параллелепипеда
12
Нахождение площади поверхности параллелепипеда
13
Нахождение суммы длин всех рёбер параллелепипеда
Раздел 4: Уравнения
Уравнением, называется равенство , содержащее неизвестное , значение которого нужно найти.
Корнем уравнения называется значение буквы , при котором уравнение становится верным числовым равенством .
Решить уравнение – значит найти все его корни или убедиться ,что их вообще нет.
Пример1: 0 * х = 12 . Это уравнение не имеет корней , т.к. при умножении нуля на число получают нуль , и число 12 никогда не получат.
Пример 2 : 0 * х = 0 . Это уравнение имеет бесконечное множество корней , т.к. при умножении нуля на любое число мы всегда получаем нуль.
а) простейшие уравнения:
Чтобы найти вычитаемое , нужно из уменьшаемого вычесть разность. 346 – х = 259 х = 346 – 259 х = 87 Ответ : х = 87 чтобы найти уменьшаемое , нужно к разности прибавить вычитаемое. х – 250 = 52 х = 250 + 52 х = 302 Ответ: х = 302 Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель. 5*х = 500 х = 500 : 5 х = 100 Ответ : х = 100 Чтобы найти неизвестное слагаемое , нужно от суммы вычесть известное слагаемое. 64 + х = 146 х = 146 – 64 х = 82 ответ: х = 82
Чтобы найти делитель , нужно делимое разделить на частное. 240 : х = 20 х = 240 : 20 х = 12 Ответ : х = 12 Чтобы найти делимое , нужно частное умножить на делитель. х : 18 = 6 х = 6 * 18 х = 108 Ответ : х = 108
б) Примеры решения сложных уравнений:
( х – 50 ) + 41 = 95 , где х -50 –слагаемое х -50 = 95 – 41 х – 50 = 54 , где х - уменьшаемое х = 54 + 50 х = 104 Ответ : х = 104 77 : ( х + 10 ) = 7 , где х + 10 – делитель х + 10 = 77 : 7 х + 10 = 11 , где х – слагаемое х = 11 – 10 х = 1 Ответ : х = 1 83 – ( х – 42 ) = 12 , где х – 42 –вычитаемое х – 42 = 83 – 12 х – 42 = 71 , где х – уменьшаемое х = 71 + 42 х = 113 Ответ : х = 113 ( 13 + х ) – 58 = 126 , где 13+х -уменьшаемое 13 + х = 126 + 58 13 + х = 184 , где х - слагаемое х = 184 – 13 х = 171 ответ : х = 171
95 – ( 99 – х ) = 8 , где 99 – х – вычитаемое 99 – х = 95 – 8 99 – х = 87 , где х – вычитаемое х = 99 – 87 х = 12 ответ : х = 12
8 * ( х – 14 ) = 56 , где х – 14 – множитель х – 14 = 56 : 8 х – 14 = 7 , где х – уменьшаемое х = 7 + 14 х = 21 Ответ : х = 21
х : 8 – 6 = 49 , где х : 8 – уменьшаемое х : 8 = 49 + 6 х : 8 = 55 ,где х – делимое х = 55 * 8 х = 440 Ответ : х = 440 52 + 72 : х = 56 , где 72 : х – слагаемое 72 : х = 56 – 52 72 : х = 4 , где х – делитель х = 72 : 4 х = 18 Ответ : х = 18
Раздел 5 : Решение задач с помощью уравнений
Типы задач:
1) Задачи с одной переменной
На полке стояли книги. После того , как с полки взяли 12 книг , а поставили – 9 , на полке стало 39 книг. Сколько книг стояло на полке сначала?
Было
Взяли
Поставили
Стало
?
12 книг
9 книг
39 книг
Решение:
Пусть было Х книг , тогда ( Х – 12 ) + 9 = 39
Х – 12 = 39 – 9
х – 12 = 30
х = 30 + 12
х = 42 ( книг ) – было
Ответ: 42 книги.
2) Задачи с двумя одноименными величинами
На двух полках стояло 72 книги. На второй полке стояло в 2 раза больше , чем на первой . Сколько книг стояло на каждой полке?
Первая полка
?
 72 книги
72 книги
Вторая полка
? , в 2 раза больше , чем
Решение:
Пусть на первой полке стояло Х книг , тогда на второй стояло (2х) книг. Всего на полках стояло 72 книги. Составим уравнение: х + 2х = 72
х ( 1 + 2 ) = 72
3х = 72
х = 72 : 3
х = 24 ( книг ) – на 1 – й полке
2) 24 * 2 = 48 ( кн.) – на 2-й полке Ответ: 24 книги, 48 книг.
3) Задачи с тремя зависимыми величинами
а) За 2 кг яблок и 3 кг груш заплатили 31 руб. Сколько стоит килограмм яблок и килограмм груш , если груши дороже яблок на 2 руб.
Фрукты
Цена 1 кг
Количество
Стоимость
Яблоки
?
2 кг
 31 грн.
31 грн.
груши
? , на 2 руб. больше
3 кг
Решение: Пусть 1 кг яблок стоит х ( руб.) , тогда 1 кг груш стоит ( х + 2 ) руб. За 2кг яблок заплатили ( 2х ) руб.) , а за 3 кг груш – 3* ( х + 2 ) руб .За всю покупку заплатили 31 грн. Составим уравнение : 2х + 3 ( х + 2 ) = 31
2х + 3х + 6 = 31
5х + 6 = 31
5х = 31 – 6
5х = 25 ; х = 25 : 5 ; х = 5 ( руб.) – стоит 1 кг яблок
2) 5 + 2 = 7 ( руб.) – стоит 1 кг груш Ответ : 5 руб., 7 руб.
б) Два велосипедиста одновременно выехали навстречу друг другу из сёл, расстояние между которыми 50 км. Встретились они через 2 часа . Первый ехал со скоростью 12 км/ч. найдите скорость второго велосипедиста.
Велосипедист
скорость
время
расстояние
первый
12мк/ч
2ч
 50 км
50 км
второй
?
2ч
Решение :
Пусть скорость второго велосипедиста – х км/ч , тогда он поехал ( 2х ) км , а первый проехал – (12 * 2 ) км. Общее расстояние 50 км. Составим уравнение:
2х + 12 * 2 = 50 ;
2х + 24 = 50 ;
2х = 50 – 24
2х = 26
х = 26 : 2
х = 13 ( км/ч) – скорость второго велосипедиста. Ответ : 13 км/ч.
в) Катер прошел 51 км по течению реки и потратил на это 3 часа. Найдите скорость течения , если собственная скорость катера равна 15 км/ч.
Движение
скорость
время
расстояние
По течению
(15 + ?) км/ч
3 часа
51 км
Решение:
Пусть скорость течения – х км/ч, тогда скорость по течению равна ( 15 + х ) км/ч. Расстояние катера по течению реки составляет 3 * ( 15 + х ) км. Составим уравнение: 3 * ( 15 + х ) = 51
15 + х = 51 : 3
15 + х = 17
х = 17 – 15
х = 2 ( км/ч ) – скорость течения реки Ответ: 2 км/ч.
ПАМЯТКА ДЛЯ УЧЕНИКА
Скорость по течению равна течение 2 км/ч катер10 км/ч Скорость против течения равна течение3км/ч катер 24км/ч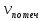 =
=  +
+ 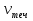
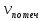 = 2 + 10 = 12 ( км/ч
= 2 + 10 = 12 ( км/ч  =
= 
 = 24 – 3 = 21 км/ч
= 24 – 3 = 21 км/ч

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ