Урок "Путешествуем по графам"
Урок "Путешествуем по графам"
Цель:
повторить и закрепить сведения о графах, полученные на предыдущих уроках;
развивать умение самостоятельно строить графы по словесному описанию отношений между предметами и существами;
познакомить детей с понятием и “путь в графе”;
научить строить и описывать пути в графах;
повысить мотивацию учебно-познавательной деятельности школьников к информатике посредством компьютерной поддержки.
Задачи:
Образовательные: продолжить знакомство с графом; формировать умения анализировать, строить графы по словесному описанию отношений между предметами и существами, обобщать предложенный материал.
Развивающие: развивать умение применять полученные знания на практике при решении графических задач, познавательный интерес к учебному предмету, творческую активность, логическое мышление, внимание.
Воспитательные: способствовать формированию самооценки четвероклассников, воспитывать взаимопомощь и способность к сотрудничеству.
1.Повторение.
Учитель: На прошлом уроке мы начали изучать графы.
Кто из вас может сказать:
– что такое “граф”;
– как называются точки в графах;
– как называются линии в графах.
(Слайд1,2)
-Приведите примеры графов. Где в жизни мы с ними встречаемся? 
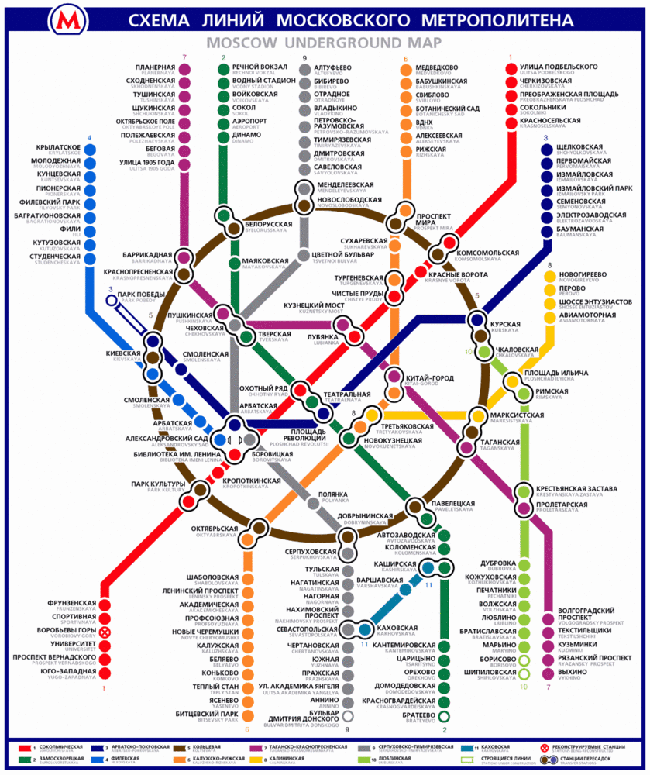
(Слайд 3, 4, 5)
2. Работа на интерактивной доске.
-А сейчас давайте с вами построим граф на интерактивной доске. Кто мне поможет?
У.:Представим себе, что между 3 и 4 классами проходят соревнования по пионерболу.
На схеме классы обозначены точками:
4А, 4Б, 3А, 3Б, 3В.
Послушайте задание:
4А играет с 4Б, 3А с 3Б, 3Б с 3В.
Что получилось? (граф)
Таким образом, игры или отношения между классами мы обозначаем линиями. Получается граф, где вершины графа обозначают классы, а ребра-связи, отношения между классами, т.е. игры.
Учитель подытоживает сказанное учениками:
– Итак: вершины графа обозначают предметы или существа, а рёбра- связи, отношения между ними.
3.Проверка домашнего задания. (Слайд 8)
- Почему майка у Ника жёлто-синяя? (в его плане не 4 хода и есть ход к коту).Почему в руках у него зелёный шарик? (В плане не 4 хода или есть код к коту)…Скажите, а какой цвет получится, если соединить синий и жёлтый? (зелёный, майка Ника зелёная)…
4. Изучение нового.
– Отношения в графе изображаются при помощи линий. Мы называем их рёбра. Одни отношения изображаются рёбрами без стрелок, а другие – рёбрами со стрелками.
Работа по учебнику, с.11 №13.
(Слайд 9)
Прочитайте задание:
Проведите линию от описания к графу.
-Почему к первому описанию относится граф со стрелками, а ко второму – без стрелок?
Вопрос:
Между какими отношениями в графах нужны стрелки?
Ответ: Стрелки нужны, когда мы обозначаем порядок действия или путь от одной вершины графа к другой, потому что путь имеет направление. Например один шахматист сыграл и победил, один человек позвонил другому, один приходится другому сыном и т.д.
А если два человека относятся друг к другу одинаково, один приходится другому братом, то стрелка не нужна.
5. Игра «Нужна ли стрелка?» (Учебник с.123)
Я привожу примеры отношений между существами или предметами, а вы говорите, нужна ли стрелка на ребре этого графа или не нужна.
- друг сообщил другу какую-то новость;
- Лена и Лиза – сестры;
- один игрок бросил мяч другому;
- два человека – отец и сын;
- строитель построил дом;
- две книги стоят на одной полке;
- два человека живут в соседних домах.
6.Вводится понятие “Направленное ребро”.
Линия со стрелкой в графе – это направленное ребро.
Направленное ребро – это ребро, которое имеет направление.
(Ученики приводят свои примеры.Демонстрация слайдов презентации не моей)
Учитель: направление в графах задаётся стрелочками, но не всегда у графа могут быть рёбра (Слайд 10) в отличие от вершин. Такой граф называется пустым.


7. Мы продолжаем путешествие по графу.стр. 12
На прошлом уроке вы решили, что лучший план строительства ходов - это план…Джека. Почему? (Каждый мышонок согласен вырыть один ход и никто не хочет попасть в лапы коту).
Сегодня мышата готовы начать строительство ходов, но у них одна лопата и поэтому им придётся копать по очереди. По готовому плану Джека мы попробуем построить графы для двух способов передачи лопаты.
Прочитайте задание 14.
-Найдите подсказку в тетрадях: кто при этом должен копать первым? Подсказка приведена в первой строке описания пути – Пухлик.
-Можно ли изобразить путь лопаты ребрами без стрелок? Почему? (путь от одной вершины графа к другой можно изобразить только с помощью ребер со стрелками, потому что путь имеет направление).
-Теперь давайте попробуем описать путь, перечисляя по порядку обозначения вершин этого графа.
- Помощники! Помогите! (Работа на интерактивной доске)
-Чем отличаются два пути лопаты? (начинаются и заканчиваются оба пути одинаково, но в первом случае сначала копает Джек, а потом Мауси, а во втором случае – наоборот).
Прочитайте задание 15.
Прочитать задание вслух.
-Ребята найдите и покажите на доске такую вершину, из которой выходят три стрелочки? (вершина справа от буквы «Т»).
-К каким буквам ведут стрелки от этой вершины? (к буквам «П», «С» и «Т»).
-Какая же буква должна быть в этой вершине? (это должна быть такая буква, чтобы из неё можно было получить букву «П», «С» или «Т», добавив одну черточку.Можно рассуждать наоборот: если убрать по одной черточке в буквах «П», «С» и «Т», то получится искомая буква.)
-Вам понятно как делать. Теперь самостоятельно определите и заполните остальные пустые вершины графа у себя в тетради.
8. Домашнее задание. Дома вы будете выполнять задание 13(придумать историю к 5 графу), 15, 16, 17. Откройте, посмотрим, что вам нужно сделать.
-В 16 задании вам нужно будет заменить семерку на единицу.
-Каждая стрелка означает, что в числе одна семерка заменяется на единицу и получается другое число.
-Сейчас мы с вами вмести впишем числа и разберем один путь.
-А 17 задании вам нужно будет нарисовать домик не отрывая руки и не обводить одно ребро дважды. Потом записать путь нарисованного домика.
-Все остальное делается аналогично.
9. Подведение итогов.
-Чему сегодня учились на уроке?
(вспомнили, между какими отношениями в графах нужны стрелки
…узнали, что такое направленное ребро, учились описывать пути в графах, перечисляя по порядку обозначения вершин, также мы вспомнили из каких элементов состоит граф…

Нравится материал? Поддержи автора!
Ещё документы из категории начальная школа:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ