Муниципальное бюджетное общеобразовательное учреждение

Троицкая средняя общеобразовательная школа

Некоторые методы решения

олимпиадных задач.

(для 5-7 классов)

Автор: Зубова Анна Николаевна

учитель математики

с. Троицкое

2013г.

Содержание

Введение…………………………………….…………………………………...3

Основная часть

Олимпиадные задачи……………………………………….……………………4

Анкетирование учащихся………………………………………………………..6

Изучение типов олимпиадных задач и методов их решения………………….8

Выводы ……...…………………………………………………..........................18

Памятка участнику олимпиады ………………………………………………...18

Список литературы ………………………………………………………….…..19

Введение

Каждый год в школе проводится I тур математической олимпиады, затем муниципальная олимпиада и т.д. Внешняя простота таких задач — их условия — обманчива. Кто хотя бы раз в жизни пробовал решать математические олимпиадные задачи, тот понимает, о чем идет речь. Олимпиадные задачи, как правило, являются нестандартными, т.е. требующими использования всех знаний в нестандартных ситуациях, но в школьном курсе математики этому вопросу внимания практически не уделяется. Поэтому я решила разобраться в решении этих задач, попробовать их исследовать, найти общие идеи и методы решения.

Цель: исследование и изучение основных типов олимпиадных задач, ознакомление с методами их решения и развитие познавательного интереса учащихся к такому виду задач.

Были поставлены такие задачи:

- изучить и понять типы олимпиадных задач;

- выявить отношение учащихся к такому виду задач;

- рассмотреть идеи и методы решения олимпиадных задач;

- наработать навыки в решении таких задач (выпуск методички).

Объект: разные олимпиадные задачи: логические задачи, задачи на переливание и взвешивание, задачи с отношениями, задачи на чет и нечет, задачи на делимость, раскраски в шахматном порядке. А предмет исследования - способы решения таких задач.

Актуальность. Две стихии господствуют в математике - числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. Задача- это почти всегда поиск, раскрытие каких-то свойств и отношений, а средства её решения- это интуиция и догадка, эрудиция и владение методами математики. Эти же качества человеческого ума воспитываются, укрепляются, обогащаются у каждого, кто регулярно отдает часть своего досуга умственной гимнастике, лучшим видом которой является решение математических головоломок, ребусов, задач с интригующим содержанием.

Гипотеза: Изучение методов решения олимпиадных задач повысит интерес учащихся к принятию участия в них; способствует развитию компетентной личности, владеющей настойчивостью, инициативой, самостоятельностью.

Методы изучения нашей проблемы:

Поисковый метод с использованием научной и учебной литературы;

Исследовательский метод при определении видов олимпиадных задач и методов их решений;

Практический метод решения задач.

Олимпиадные задачи.

Что же мы понимаем под олимпиадными задачами?

Олимпиадные задачи в математике — термин для обозначения круга задач, для решения которых обязательно требуется неожиданный и оригинальный подход.

Математические соревнования и конкурсы имеют давнюю историю. Так сохранились сведения о том, что уже в древней Индии (около 2000 г. До н.э.) для решения математических задач устраивались состязания в присутствии многочисленных зрителей. Широкое распространение получили математические турниры в эпоху возрождения. Школьные математические олимпиады берут свое начало с так называемого «этвёшского соревнования», проведенного в 1894 г. в Венгрии по инициативе Лорана Этвёша – президента Венгерского физико-математического общества. В СССР первые математические соревнования школьников состоялись в Грузии. В 1933 г. в Тбилиси были проведены первые школьные и районные олимпиады. Первые городские олимпиады состоялись в Тбилиси и Ленинграде в 1934 г. на следующий год в Москве и Киеве. В дальнейшем олимпиадное движение распространилось по всей стране. Идея объединить олимпиадное движение в масштабе всей страны впервые была реализована в 1960 г. и начиная с 1961 г. регулярно стали проводиться так называемые Всероссийские математические олимпиады.

На выполнение олимпиадных задач отводится строго определенное время, в качестве заданий предлагаются не задачи обязательного или повышенного уровня (по школьным меркам), а задания нестандартные.

Какая же задача называется нестандартной? «Нестандартные задачи- это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения.» (Фридман Л.М. Турецкий Е.Н. Как научиться решать задачи.- Москва. Просвещение 1989г). Однако, следует заметить, что понятие «нестандартная задача» является относительным. Одна и та же задача может быть стандартной или нестандартной, в зависимости от того, знакомы ли мы со способами решения задач такого типа. Таким образом, нестандартная задача- это задача, алгоритм которой неизвестен, т.е. неизвестен ни способ её решения, ни то, на какой учебный материал опирается решение. А многие задачи требуют и специальных знаний, подготовки. К таким задачам относятся задачи на смекалку, на логику, применения инвариантов, задачи на раскраски, чет и нечет и т.д. Конечно, для успешного решения любой задачи нужно уметь думать, догадываться, но этого мало. Нужны знания и опыт в решении задач. Полезно владеть и определенными общими подходами к решению таких задач. Поэтому мы решили разобраться в решении этих задач, попробовать их исследовать, найти общие подходы. Любая задача должна чему-нибудь научить. Решение каждой задачи должно быть шагом вперед в развитии математических знаний, умений и навыков, должно обогащать знания и опыт, учить ориентироваться в различных ситуациях.

Сложность олимпиадной задачи – это объективная характеристика задачи, определяемая ее структурой. Сложность задачи зависит от:

- объема информации(числа понятий, суждений и т.п.), необходимого для ее решения;

- числа данных в задаче;

- числа связей между ними;

- количества возможных выводов из условия задачи;

- количества взаимопроникновений при решении задачи;

- длины рассуждений при решении задачи;

-общего числа шагов решения, привлеченных аргументов и т.д.

Трудность олимпиадной задачи – субъективная характеристика задачи, определяемая взаимоотношениями между задачей и решающим ее учеником. Трудность задачи зависит от:

- сложности задачи (сложная задача, как правило, является более трудной для учащихся);

- времени прошедшего после изучения материала, который встречается в тексте задачи (задачи на материал, изученный 1-2 года назад, используемые факты, которые уже забылись);

- практики в решении подобного рода задач;

- уровня развития ученика (задача, тяжелая для ученика общеобразовательного класса, может быть легкой для ученика физико-математического класса);

- возраста учащегося.

Анкетирование учащихся.

Нами, предварительно было проведено анкетирование по отношению учащихся 5-7 класса к решению олимпиадных задач.

Анкета для учащихся.

Желали бы вы принять участие в математической олимпиаде!

Да / Нет Почему______________________________________________________________

(нужное подчеркнуть)

________________________________________________________________________________

В опросе принимало участие 52 учащихся .

Желание участвовать в олимпиаде по математике распределилось следующим образом по классам:

5 класс - 66%

6 класс -75%

7 класс – 38 %

При ответе «Нет» учащиеся давали следующие пояснения: такие задачи на уроках не решают; никогда не встречал таких задач; задачи слишком трудные для меня; не знаю с чего начать; очень сложно; наберу меньше всех баллов – будут смеяться.

Ребятам желающим принять участие были предложены по классам олимпиадные задачи различных типов. Выполнение которых отражено в таблице.

Тип задачи выполнение

числовые ребусы

63%

арифметика

35%

на взвешивания и переливания

21%

логические задачи

14%

на движение или работу

42%

на раскраску или разрезание

21%

на четность или делимость

7%

геометрические

28%

Результаты мы представим в виде диаграммы

Из диаграммы видно, для ребят более легкими являются такие задания как числовые ребусы, задачи на движение и работу, т.е., с которыми они встречались в ходе учебных занятий, остальные задания вызывают большие затруднения. Ребят которые справились со всеми заданиями нет, что подтверждает наличие затруднений у ребят при решении олимпиадных задач.

Основные типы и методы решения задач

В ходе изучения научной литературы нами были выявлены следующие типы олимпиадных задач для учащихся 5-7 класса:

• Числовые ребусы;

• Арифметика

• Задачи на взвешивание, переливания;

• Логические задачи;

• Задачи на движение или работу;

• Задачи на раскраску или разрезание;

• Задачи содержащие идеи четности или делимости;

• Задачи на проценты и отношения

• Задачи, решаемые с конца

• Геометрические задачи;

Математическими ребусами называются задания на восстановление записей вычислений. Условие ребуса либо целиком зашифрованную запись, либо только часть записи. Записи восстанавливаются на основании логических рассуждений. При этом нельзя останавливаться отысканием только одного решения. Испытание надо доводить до конца, чтобы убедиться, что нет других решений, или найти все решения.

Задача: Какую цифру заменяет черный треугольник?

В примере на сложение:

► + ► + ○○ = Δ Δ Δ

различные фигурки заменяют различные цифры. Какую цифру заменяет черный треугольник?

Решение: Максимальное значение суммы трех наших слагаемых равно 9 + 9 + 99 = 117. Значит, Δ Δ Δ = 111. Минимальное значение числа ○○ равно 111 - 9 - 9 = 93, а само число равно 99. На долю одного черного треугольника приходится (111 - 99) : 2 = 6.

Арифметика. Для решения задачи нужно уметь выполнять арифметические операции, как правило над числами с большим количеством цифр, а так же операции с дробями.

Задача: Автобусный билет будем считать счастливым, если между его цифрами можно в нужных местах расставить знаки четырёх арифметических действий и скобки так, чтобы значение полученного выражения равнялось 100. Является ли счастливым билет N123456?

Решение:

1 + (2 + 3 + 4) . (5 + 6) = 100. Есть и другие решения

Задачи на взвешивания – достаточно распространенный вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой.

Задача: У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?

Решение: Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена.

Задачи на переливания – задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости, которые решаются с помощью алгебраического метода.

Задача: Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?

Решение:

Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л.

Решение лучше и удобнее оформить в виде таблицы:

Шаг

Сосуд – 3л

Сосуд – 5л

1

0

5

2

3

2

3

0

2

4

2

0

5

2

5

6

3

4

Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена.

Логические задачи:

Существует множество разных логических задач. В ходе знакомства с ними, я выделила несколько основных типов задач:

«Правдивые задачи». В этих задачах нужно определить, какое выражение истина. Такие задачи могут иметь разную форму, но в них есть одна общая часть. В условие будет сказано, что есть человек, говорящий всегда правду, и его антагонист, говорящий всегда неправду.

Задача: В одном городе кто-то угнал машину у градоначальника. Полиция задержала троих человек: Джона, Джека и Джо. Полиции было известно, что один из них - лжец, один - всегда говорит правду, а про третьего точно неизвестно, говорит ли он правду или ложь. Полиция также знала, что один из них угнал машину, и что этот человек всегда говорит правду. Три человека сказали следующее:

Джон: Я не виновен.

Джек: Он говорит истинную правду.

Джо: Я угнал машину.

Кто угнал машину и кто лжец?

Решение: Джон сказал: "Я не виновен". По условию задачи два человека являются невиновными: лжец и шутник. Джон не может быть лжецом, так как лжец, в данном случае, сказал бы, что он виновет. Джон не может быть и правдолюбцем, так правдолюбец виновен, и он не сможет сказать неправду. Остается, что Джон шутник, при этом он говорит правду, так как он, действительно невиновен. Джек подтверждает невиновность шутника Джона, т.е. Джек говорит правду, поэтому он не лжец, а правдолюбец, Джек и угнал машину. Джо - лжец и как положено лжецу, он всех обманывает, говоря, что он угнал машину.

Задачи на вычисление соотношения, которые решаются методом таблиц и графов.

Метод таблиц, который очень удобен при решении задач на соотношение. Его выгода в наглядности логических размышлений, возможности контролировать цепочку рассуждений, а также возможность формализовать некоторые новые логические суждения.

Задача: Живут-поживают пять зайчат: Попрыгунчик, Ушастик, Тишка, Зайка, Беляк, и у каждого есть мячик. Цвета мячиков такие: синий, зеленый, красный, желтый и оранжевый. У Ушастика мячик желтого цвета, а у Зайки не зеленый, не синий и не красный. У Попрыгунчика был бы синий мячик, если бы у беляка был зеленый мячик, но у беляка мячик другого цвета. Беляк не любит игрушки синего цвета. У кого какой мячик?

Решение: У Ушастика желтый мячик. (Ставим плюс в Ячейку «Желтый, Ушастик», а во все остальные ячейки столбца «Ушастик» и строку «Желтый» заполняем минусами). У Зайки не зеленый, не синий и не красный мячик, значит – оранжевый. (Ставим плюс в ячейку «Оранжевый, Зайка», заполняем свободные ячейки столбца и строки минусами). Так как у Беляка мячик не зеленый и не синий(ставим минусы), не желтый и не оранжевый, значит у него мячик красного цвета. Так как у Прыгунчика не синий мячик, значит у него зеленый. Получаем, что у Тишки мячик синий.

Цвет мячика

Кличка зайчика

Прыгунчик

Ушастик

Тишка

Зайка

Беляк

Зеленый

+

-

-

-

-

Синий

-

-

+

-

-

Красный

-

-

-

-

+

Желтый

-

+

-

-

-

Оранжевый

-

-

-

+

-

Метод граф. Граф – очень популярный объект в математике – есть набор точек, соединенных отрезками – ребрами. Граф отлично моделирует передвижения объекта между географическими объектами, компьютерные сети, знакомства, отношения. Графы помогают лучше понять структуру исследуемого объекта.

Задача: В школьной столовой на первое можно заказать щи, гороховый суп и борщ, на второе – котлету и рыбу, а на третье - чай и морс. Сколько вариантов обеда можно получить из указанных блюд?

Обед

Борщ Гороховый суп Щи

Рыба Котлета Рыба Котлета Рыба Котлета

Морс Чай Морс Чай Морс Чай Морс Чай Морс Чай Морс Чай

Ответ: 12 вариантов

Метод Кругов Эйлера. Круги Эйлера – задачи на пересечение или объединение множеств. Это геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.

Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.

Задача: Часть жителей города умеет говорить только по-русски, часть – только по-узбекски и часть умеет говорить на обоих языках. По-узбекски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?

Решение: Составим схему –

У ? Р

85% 75%

В кружке под буквой «У» обозначим жителей, говорящих по-узбекски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «У» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).

Задачи на движение. Во всех таких задачах допускается определенная идеализация: считается, что тела движутся прямолинейно и равномерно, скорости (в том числе скорость течения) постоянны в течение определенных промежутков времени, не меняются при поворотах и т.д., Основными типами задач на движение являются следующие:

1) задачи на движение по прямой (навстречу и вдогонку),

2) задачи на движение по воде,

3) задачи на среднюю скорость.

Задача: Таракан Валентин объявил, что умеет бегать со скоростью 50 м/мин. Ему не поверили, и правильно: на самом деле Валентин всё перепутал и думал, что в метре 60 сантиметров, а в минуте 100 секунд. С какой скоростью (в "нормальных" м/мин) бегает таракан Валентин?

Решение: Валентин пробегает 50*60=3000 см за 100 с, то есть его скорость 30 см/с, что составляет 18 м/мин.

Задачи на работу

Такие задачи часто вычисляются по формуле: А=P×t где P – производительность труда, т. е. часть работы, выполняемая в единицу времени; t – время, необходимое для выполнения всей работы.

Пусть P×t=1 – взаимообратные величины, т. е. вся работа А=1, следовательно: P=A/t=1/t t=A/P=1/P

Задача: Котенок Малыш может облизать себя с головы до кончика хвоста за полчаса, а кот Тоша может облизать Малыша за 5 минут. Себя Тоша способен помыть за 20 минут. Сколько времени придется трудиться Малышу, чтобы помыть Тошу?

Решение: Малыш облизывает сам себя в 6 раз (30мин/5мин=6) медленнее, чем его облизывает кот Тоша. Тоша облизывает себя за 20 минут. Следовательно, Малыш оближет кота Тошу за 20мин · 6=120мин=2часа.

Задачи на раскраску. Суть данного метода состоит в следующем. Раскрасив некоторые ключевые элементы, которые фигурируют в задаче в несколько цветов, исследовать, что будет происходить, если выполнять условия задачи. Цвет позволяет значительно упростить понимание процесса, фигурируемого в условии, и зачастую приводит к решению. Этот метод позволяет эффективно решать ряд задач, в частности, игровые и шахматные задачи.

Задача: В каждой клетке доски 5×5 клеток сидел жук. Затем каждый жук переполз на соседнюю (по стороне) клетку. Докажите, что осталась хотя бы одна пустая клетка.

Решение: раскрасим доску в 2 цвета. Черных клеток-13, а белых 12. При переползании с черных клеток жуки переползали на белые и наоборот. Так как белых клеток 12, а черных на одну больше и все жуки с белых переползают на черные, то одна черная клетка останется.

Ответ : останется 1 черная клетка.

Задачи на разрезание. В этих задачах требуется разрезать данную фигуру на части, из которых можно сложить другую, уже заданную плоскую фигуру так, чтобы обе фигуры были равносоставленными, т. е. состояли из неперекрывающихся частей без свободных промежутков. Для решения задач на разрезание не существует универсального метода и каждый кто берется за них должен проявить смекалку и инициативу.

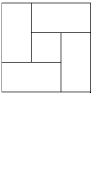
Задача 2: Сделайте из квадрата четыре равных прямоугольника и один квадрат. Решение:

Задачи на четность. Многие задачи легко решаются, если заметить, что некоторая величина имеет определённую чётность. Из этого следует, что ситуации, в которых данная величина имеет другую чётность, невозможны. Иногда эту величину надо «сконструировать», например, рассмотреть чётность суммы или произведения, разбить объекты на пары. Заметить чередование состояния, раскрасить объекты в два цвета и т.д.

Задача: Кузнечик прыгал вдоль прямой и вернулся в исходную точку (длина прыжка 1м). Докажите, что он сделал чётное число прыжков.

Решение: Поскольку кузнечик вернулся в исходную точку. Количество прыжков вправо равно количеству прыжков влево, поэтому общее количество прыжков чётно.

Задачи на делимость. Необходимо знать признаки делимости и теоремы:

1. Если каждое слагаемое суммы делится на одно и то же число, то и сумма делится на это число.

2. Если уменьшаемое и вычитаемое делятся на одно и то же число, то и разность делится на это число.

3. Если в произведении нескольких натуральных чисел хотя бы один из сомножителей делится на какое-то число, то и все произведение делится на это число.

4. Если некоторое целое число делится на другое, а это другое – на третье, то и первое число делится на третье.

Основываясь на известных нам признаках делимости и теоремах 1-4, можно сформулировать и признаки делимости на 4, на 6, на 8, на 15 и другие.

Задача: Найти наименьшее натуральное число, которое при делении на 7 дает в остатке 6, а при делении на 9 остаток равен 8.

Решение: В обоих случаях - как при делении искомого числа на 7, так и при делении его на 9 остаток на единицу меньше делителя. Увеличив делимое на 1, получим число, которое делится без остатка и на 7, и на 9. Наименьшее такое число - 63. Искомое число на 1 меньше и равно 62.

Задачи на проценты и отношения. Решение задач на применение основных понятий о процентах и отношениях.

Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь

Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.

Правило 3. Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%.

Задача: Влажность купленного арбуза составила 99%. В результате длительного хранения влажность снизилась до 98%. Как изменилась масса арбуза?

Решение: Свежий арбуз на 99% процентов состотит из жидкости и на 1% - из сухой массы. В результате усушки количество жидкости уменьшилось и составило 98% от новой, также уменьшившейся массы арбуза. Количество же сухого вещества, оставаясь неизменным, составило 2% от новой массы арбуза. Процентное содержание в арбузе сухого вещества (при неизменной его массе) увеличилось вдвое. Следовательно масса арбуза в результате усушки уменьшилась вдвое.

Задача: Условие В классе учится меньше 50 школьников. За контрольную работу седьмая часть учеников получила пятёрки, третья — четвёрки, половина — тройки. Остальные работы были оценены как неудовлетворительные. Сколько было таких работ?

Решение: Поскольку число школьников, получивших ту или иную оценку, всегда целое, то для решения задачи нам надо найти целое число, меньшее 50, одновременно делящееся на 7, 3, 2. Единственным возможным ответом является число 42. Это значит, что всего в классе 42 ученика; 6 из них получили пятёрки; 14 — четвёрки; 21 — тройки. Следовательно, двойку получил 1 ученик.

Задачи, решаемые с конца. Если в задаче задана некоторая операция, и она обратима, то можно сделать «обратный» ход от конечного результата к исходным данным. (Например, надо вынести шкаф из комнаты. Пройдёт ли он через дверь? Пройдёт, потому что через дверь его внесли). Анализ с конца используют при поиске выигрышных и проигрышных ситуаций.

Задача: Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Дедка, Бабка, Внучка, Жучка и Кошка вместе с Мышкой могут вытащить Репку, а без Мышки — не могут. Сколько надо позвать Мышек, чтобы они смогли сами вытащить Репку?

Решение: Кошка заменяет 6 Мышек. Жучка заменяет 5•6 Мышек. Внучка заменяет 4•5•6 Мышек. Бабка заменяет 3•4•5•6 Мышек. Дедка заменяет 2•3•4•5•6 Мышек. Итого потребуется:

(2•3•4•5•6) + (3•4•5•6) + (4•5•6) + (5•6) + 6 + 1 = 1237 Мышек.

Геометрические задачи.

Пожалуй, самыми интересными и сложными среди олимпиадных задач являются задачи по геометрии. Мы не будем разбирать сложные задачи, ограничившись только отдельными подходами к решению геометрических задач. Даже их классификация представляет затруднения. Некоторые из задач можно назвать задачами геометрическими условно, ведь они сводятся к элементарным вычислениям. В таких задачах важнее всего идея решения.

Задача : Размышляем над кубиком

От кубика, склеенного из бумаги, отрезали уголок.

Этот кубик разрезали по некоторым ребрам, развернули и получили одну из фигурок A - E.

Какую?

ответ Е

Памятка участнику олимпиады.

1. Прочитайте все задачи и наметьте, в каком порядке вы будете их решать. Помните последние задачи обычно более сложные.

2. Если для вас задача решалась слишком легко, то, скорее всего вы не поняли условие или где-то ошиблись.

3. Если задача не решается – попробуйте упростить ее условие (взять меньшие числа, рассмотреть частные случаи и т.д) или порешать ее «с конца», «от противного», поставить вместо чисел переменные и т.д.

4. Не зацикливайтесь на на одной задаче: иногда отрывайтесь от нее и оценивайте положение. Если есть хоть небольшие успехи, то можно продолжать, а если мысль ходит по кругу, то задачу лучше оставить, хотя бы на время.

5. Почувствовав усталость – отдохните (посмотрите в окно, закройте глаза, отвлекитесь).

6. Решив задачу, сразу оформите ее решение. Это поможет проверить рассуждения и освободить мысли для других задач.

7. Перед сдачей работы, проверьте еще раз написанное – поймут ли ваши решения задач члены жури?

Список литературы

1. Канель-Белов А. Я., Ковальджи А. К. Как решают нестандартные задачи / Под ред. В. О.Бугаенко.|4-е изд., стереотип.|М.: МЦНМО, 2008.| 96 c.

2. Игнатьев Е.И. В царстве смекалки / Под редакцией М.К. Потапова. – 2-е издание.- М.: Наука. Главная редакция физико-математической литературы, 1981.- 208с.

3. Петраков И.С. Математические олимпиады школьников: Пособие для учителей.- М.: Просвещение, 1982.- 96с.

4. Баранова т.А., Блинков А.Д., Кочетков К.П., Потапова М.Г., Семенов А.В. Олимпиада для 5-6 классов. Весенний тур Архимеда. Задания с решениями, технология проведения.-М.: МЦНМО – 2003г.- 125с.

5. Фарков А.В. Математические олимпиады в школе. 5-11 классы/ А.В. Фарков. -8-е изд., испр. И доп. – М.:Айрис-пресс, 2009.-256с.

6. Севрюков П.Ф. подготовка к решению олимпиадных задач по математике / П.Ф. Севрюков. –Изд.2-е. –М.: Илекса; Народное образование; Ставрополь: Сервисшкола, 2009.- 112с.

7. Шарыгин И.Ф., Шевкин А.В. Задачи на смекалку. Учебное пособие для 5–6 классов общеобразовательных учреждений. 8-е изд.-М.: Просвещение, 2006.

8. Математика.5-9 классы. Развитие математического мышления: олимпиады, конкурсы / авт.-сост. И.В. Фотина.-Волгоград: Учитель, 2010.-202.

9. Богомолова О.Б. Логические задачи /О.Б. Богомолова.-М.:БИНОМ. Лаболатория знаний, 2005. – 271с.:ил.