45

Содержание

1. Введение ……………………………………………………………………...4

1.1. Концепция тяжелоионного DT-синтеза с быстрым поджигом ………....4

1.2. Базовые пераметры ЯЭУ на основе тяжелоионного DT-синтеза …….…5

2. Физико-математическая модель сжатия и горения мишени …....................7

2.1. Взамодействие тяжелоионного пучка с оболочкой мишени ………….…7

2.2. Уравнения сохранения трехтемпературной гидродинамической

модели ……………………………………………………………………….8

2.3. Уравнения диффузии заряженных частиц и кинетики

термоядерного горения …………………………………………….……...10

3. Результаты расчетов сжатия и горения мишени …………………………...11

3.1. Динамика сжатия мишени цилиндрическим пучком ……………………11

3.2. Выход ударной волны на поверхность мишени, генерация

импульсов энергии нейтронов и рентгеновского излучения …………...13

4. Физико-математическая модель разлета мишени и испарения

защитной жидкой пленки первой стенки камеры …………………………….16

4.1. Сценарий разлета мишени и испарения защитной пленки .…………......16

4.2. Уравнения гидродинамики ………………………………………………...18

4.3. Коэффициенты вязкости и теплопроводности ……………………………19

4.4. Коэффициенты поглощения и температурной релаксации ………………20

4.5. Уравнение состояния ………………………………………………………..23

4.6. Начальные и граничные условия для расчета разлета мишени

и абляции жидкой пленки …………………………………………………..24

4.7. Алгоритм расчета и численная схема ……………………………………...25

5. Результаты расчетов разлета мишени и абляции жидкой пленки ….............26

5.1. Отклик жидкой пленки на воздействие рентгеновского

пред-импульса и нейтронного потока ……………………………………...26

5.2. Разлет облака мишени и абляция жидкой пленки …………………………27

6. Заключение …………………………………………………………………….34

Благодарности ……………………………………………………………………34

Литература………………………………………………………………………...35

1. ВВЕДЕНИЕ

1.1. Концепция тяжелоионного DT-синтеза с быстрым поджигом

Настоящая работа является продолжением исследований [1-6], в ходе которых была предложена концепция энергетической установки на основе тяжелоионного DT-синтеза, а также были проведены численные расчеты, показывающие согласованность физических параметров, определяющих технологическую схему такой установки.

Кратко опишем содержание концепции ИТИС (FIHIF), следуя [1, 5, 6].

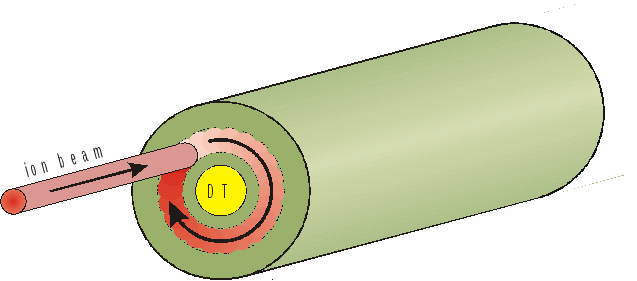
В работах [2, 7, 8] предполагается, что можно построить мощный тяжелоионный ускоритель, позволяющий ускорять однозарядные ионы тяжелых металлов до энергии 500 МэВ/на нуклон (100 ГэВ/на ядро). Пучок ионов облучает с торца цилиндрическую мишень [2, 9], на оси которой находится термоядерное топливо (эквимолярная смесь DT), окруженное свинцовой оболочкой (Рис. 1). Пятно пучка перемещается по торцу мишени по окружности с частотой ~10⁹ Гц, обеспечивая практически однородное по азимуту выделение энергии в кольцевом слое (абсорбере) оболочки. Мощность пучка профилируется по времени так, чтобы энерговыделение в абсорбере обеспечило безударное сжатие топлива [10]. При достижении максимального сжатия DT-топливо поджигается сверхмощным пучком, сфокусированным на торец DT-шнура (режим быстрого поджига). Мишени инжектируются в камеру, где происходит микровзрыв, с частотой 2 Гц.

Рис. 1. Цилиндрическая мишень в концепции ИТИС и ее облучение

ионным пучком на стадии сжатия

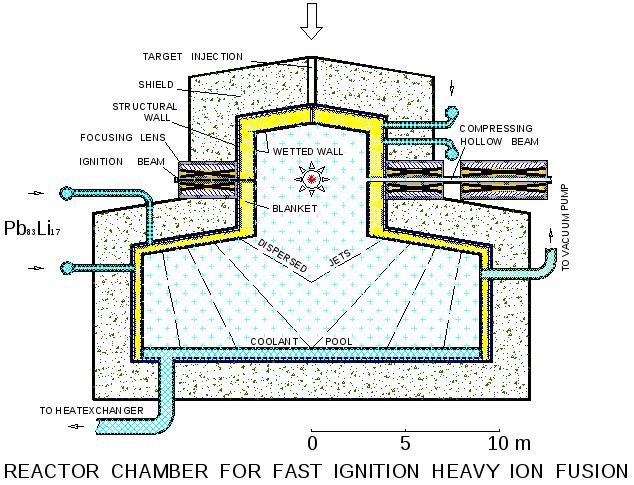
Для предложенного сочетания драйвера и мишени в работах [1, 5, 6] представлены общая схема реакторной камеры (включая первую стенку и бланкет) и тепловая схема электростанции. Первая стенка камеры выполнена из пористого карбида кремния. Через поры в камеру просачивается жидкометаллический теплоноситель (эвтектика свинец-литий), образующий защитную пленку. В нижней части камеры сделана конденсационная полость, в которую тот же теплоноситель инжектируется в виде спрэя для ускорения процесса конденсации вещества, испаренного в результате микровзрыва.

Одномерные расчеты сжатия цилиндрической мишени и двумерные расчеты ее последующего воспламенения были выполнены в работе [2]. Моделирование воздействия продуктов термоядерного микровзрыва на первую стенку камеры и конструкционные материалы бланкета реактора ИТИС было проведено в работах [4, 5] в одномерной плоской геометрии и без учета переноса излучения. В настоящей работе мы представляем результаты согласованных расчетов сжатия и горения мишени в цилиндрической постановке, а также разлет мишени - с учетом переноса нейтронов и излучения, а также отклика первой стенки камеры реактора на микровзрыв в сферически-симметричной постановке задачи.

Следует подчеркнуть, что представляемые в данной работе расчеты носят теоретический характер и не имеют верификации в части горения термоядерной мишени и, соответственно, отклика камеры на микровзрыв, поскольку требуемые параметры драйвера в настоящее время не достижимы. Кроме того, численный расчет горения и разлета носит качественный характер и не является инженерным, учитывающим реальную геометрию объекта. Целью работы было проведение сквозного расчета горения мишени, ее разлета и взаимодействия продуктов микровзрыва с материалом первой стенки камеры в идеальной математической постановке задачи, но с возможно более полной физической системой уравнений. Полученные результаты показывают, что такой расчет может быть корректно проведен. Это позволяет надеяться и на возможность проведения таких расчетов в реальной геометрии.

1.2. Базовые параметры ЯЭУ на основе тяжелоионного DT-синтеза

Для дальнейшего анализа приведем значения параметров обсуждаемой энергетической установки, следуя [6].

Драйвер. Энергетические параметры пучка тяжелых ионов (Pt или Bi):

• длительность облучения мишени 75 нс;

• средняя мощность пучка 160 ТВт;

• полное энерговложение в мишень 7,7 МДж, из них 6,0 МДж в основном пучке и 1,7 МДж в поджигающем пучке;

Мишень. Параметры цилиндрической мишени:

• длина мишени 6,4 мм;

• полная масса мишени 3,35 г;

• масса DT-топлива 5,7 мг;

• начальная плотность DT-топлива 0,05 г/см³;

• начальный радиус DT цилиндра 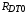=1,12 мм;

• начальный радиус мишени 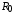=4 мм;

• степень сжатия DT-топлива по радиусу 22.

Энерговыделение в мишени:

• коэффициент выгорания DT 39 %

• полное усиление мишени 96, энерговыделение 740 МДж, в т.ч.:

• энерговыделение в термоядерных нейтронах 576 МДж;

• рентгеновское излучение 16 МДж;

• кинетическая энергия разлетающегося материала мишени 148 МДж.

Рис. 2. Камера и бланкет реактора ИТИС

Обозначения: 1 – поджигающий пучок; 2 - фокусирующие линзы;

3 - корпус-отражатель; 4 - защита; 5 - инжектор мишеней;

6 - сжимающий кольцевой пучок; 7 - к вакуумному насосу;

8 - к теплообменнику; 9 - поддон (PbLi); 10 – диспергированные

струи; 11 - бланкет; 12 - первая стенка с защитной жидкой пленкой

Камера. Камера предлагаемого реактора ИТИС имеет коаксиально-цилиндрическую конструкцию. С целью обеспечения достаточно быстрой конденсации паров область камеры разделена на две части: взрывная секция, в которой происходит собственно микровзрыв, и секция конденсации, в которой ионизованный пар конденсируется на распыляемых струях теплоносителя. Схема камеры и бланкета в рассматриваемой концепции термоядерного реактора представлена на Рис. 2.

Геометрические размеры камеры:

• радиус взрывной секции 5 м;

• высота взрывной секции 8 м;

• радиус секции конденсации 10 м;

• высота секции конденсации 8 м;

• толщина бланкета 0,5 м;

• толщина бетонной защиты 2 м.

Теплоноситель. В качестве теплоносителя предполагается использовать эвтектику Li₁₇Pb₈₃ при температуре 620 K (нижняя температура на входе в камеру) и 820 K (верхняя, на выходе из камеры). Плотность теплоносителя 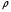=11,34 г/см³. Толщина защитной пленки первой стенки принята равной 2 мм. Удельная теплоемкость 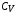эвтектики 187 Дж/кг_*K, свинца 130 Дж/кг_*K. Удельная теплота испарения свинца 0,9 МДж/кг.

2. Физико-математическая модель сжатия и горения мишени

2.1. Взаимодействие тяжелоионного пучка с оболочкой мишени

В тяжелоионном термоядерном синтезе для достижения высоких значений интенсивности облучения мишени предполагается ускорение ионов до релятивистских скоростей (0,75 скорости света при удельной энергии 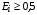ГэВ/нуклон). При этом величина массового пробега тяжелых ионов составляет 5-20 г/см². В этих условиях вполне естественным представляется сочетание цилиндрической мишени и продольного пучка ионов.

На стадии сжатия DT топлива облучение торца мишени осуществляется пучком ионов ²⁰⁹Bi c энергией E_i0 = 125 ГэВ. Пучок фокусируется в пятно диаметром 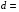1,25 мм, перемещающимся по торцевой поверхности мишени по окружности радиусом 1,875 мм с частотой вращения 1 ГГц [1]. При такой частоте вращения временной азимутальной неоднородностью энерговклада пучка ионов в оболочку мишени можно пренебречь. Радиальное распределение плотности потока энергии в пучке принимается параболическим:

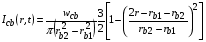, (2.1)

где 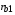и 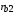– расстояния от центра мишени до границ облучающего «пятна», так что 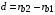есть диаметр пучка ионов. Полная мощность пучка равна

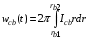. (2.2)

Удельное энерговыделение при торможении ионов определяется с учетом эффекта просветления мишени, обусловленного изменением плотности абсорбера (свинца) в процессе нагревания:

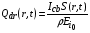, (2.3)

где 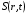– осредненная по ходу пучка в мишени тормозная способность ионов Bi²⁰⁹ в свинце

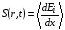, (2.4)

а сама тормозная способность определяется по формуле Бете-Блоха:

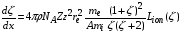, (2.5)

.

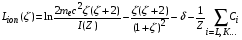Здесь 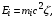где 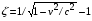; , A, Z, – соответственно плотность, атомный вес и зарядовое число ядер среды; 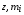– заряд и масса отдельной частицы в пучке, 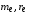– масса и классический радиус электрона; N_A – число Авогадро; I(Z) – средний потенциал ионизации атомов среды на один электрон; C_i – поправки, учитывающие связь электронов на внутренних оболочках,  – поправка на т.н. «эффект плотности», возникающая в ультрарелятивистской области энергий.

Формула (2.5) справедлива при достаточно больших скоростях ионов, когда кулоновский логарифм 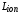существенно превышает 1, и теряет смысл при 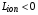. В действительности происходит «обрезание» темпа отбора энергии частицы (пик Брэгга), после чего частица замедляется с конечным темпом потери энергии.

В концепции быстрого поджига сжатое DT-топливо воспламеняется вторым пучком, соосным с мишенью и сфокусированным в пятно с диаметром, равным диаметру DT-шнура (d  100мкм). В двумерных расчетах [2] было показано, что воспламенение DT-смеси при плотности 100г/см³ происходит в окрестности брэгговского пика при удельном энерговкладе порядка 1 ПВт/мг и длительности импульса 0,3 нс. Эти параметры энерговклада используются для определения источникового члена Q_dr, который включается в правой части уравнения энергии для DT-топлива при достижении плотности 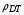=100г/см³ в одномерных расчетах данной работы.

Полная мощность пучка профилируется по времени таким образом, чтобы процесс сжатия топлива происходил при наименьшем приращении энтропии [2], и потери энергии пучка, связанные с просветлением прогреваемого материала также были минимальны.

2.2. Уравнения сохранения в трехтемпературной гидродинамической модели

Гидродинамика нагрева оболочки мишени, сжатия и горения DT смеси и нагружения материала мишени описывается одномерной трехтемпературной моделью, реализованной в коде DEIRA-4 [11].

Модель и код DEIRA-4 включают расчет температур ионов, электронов и излучения, состава, термодинамических и транспортных свойства веществ и смесей, энерговыделения в материале в результате термоядерного горения и релаксации температур. Рассчитывается кинетика термоядерного горения и диффузия быстрых заряженных частиц – продуктов горения.

Система уравнений сохранения в цилиндрической системе координат записывается в следующем виде:

уравнение сохранения массы

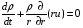, (2.6)

уравнение сохранения импульса

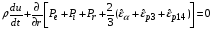, (2.7)

уравнение сохранения энергии для электронов

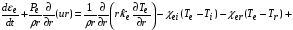
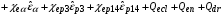, (2.8)

уравнение сохранения энергии для ионов

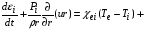
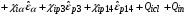, (2.9)

уравнение диффузии излучения

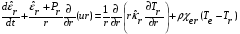. (2.10)

Здесь основные зависимые переменные

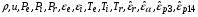
представляют соответственно средние значения плотности среды и скорости, давление электронов, ионов и излучения, внутреннюю энергию (на единицу массы среды) электронов и ионов, температуру электронов, ионов и излучения, удельную энергию излучения, внутреннюю энергию (на единицу массы среды) 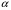-частиц и быстрых протонов с энергиями 3 и 14 МэВ.

Коэффициенты теплопроводности для электронов 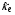и излучения 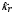являются функциями соответствующих температур и плотностей и подвергаются корректировке при соответствующих предельных значениях теплового потока. Коэффициент релаксации температур электронов и ионов 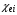является функцией температур и концентраций соответствующих частиц, коэффициент релаксации 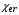является функцией температур электронов и излучения и плотности среды. Коэффициенты релаксации энергии заряженных продуктов реакции синтеза ( 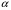частиц и протонов с энергиями 3 и 14 МэВ) 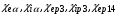и 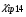зависят от температур и концентраций электронов и ионов. 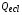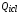Удельные источники локального энерговыделения заряженных продуктов синтеза (³He и T) и определяются из уравнений кинетики ядерного синтеза (см. ниже). 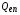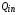Величины и представляют энерговыделение от нейтронов в DT-смеси при их взаимодействии с электронами и ионами.

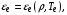
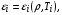
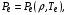
В расчетах используются затабулированные уравнения состояния для электронов и ионов 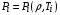. Плотность и давление излучения 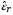и 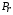связаны с температурой излучения 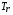формулами

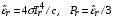. (2.11)

2.3. Уравнения диффузии заряженных частиц и кинетики термоядерного горения

Диффузионные уравнения для плотности энергии заряженных частиц 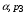и 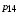записываются в нижеследующем виде (в левых частях уравнений стоят полные, т.е. лагранжевы, производные по времени):

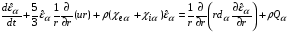, (2.12)

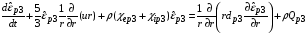, (2.13)

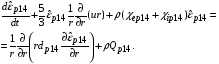(2.14)

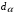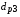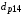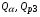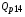Коэффициенты диффузии заряженных продуктов синтеза , и выражаются через начальную энергию и суммарный коэффициент релаксации энергии соответствующих частиц. Источники и определяются с помощью решения уравнений кинетики ядерного синтеза.

Горение термоядерного DT топлива описывается четырьмя основными ядерными реакциями:

D + T → ⁴He (3.52 MeV) + n (14.07 MeV), (2.15)

D + D → ³He (0.82 MeV) + n (2.45 MeV), (2.16)

D + D → T (1.01 MeV) + p (3.02 MeV), (2.17)

D + ³He → ⁴He (3.67 MeV) + p (14.68 MeV). (2.18)

Кинетика термоядерного горения для ядерных реакций (2.15) – (2.18) описывается уравнениями

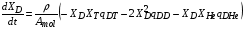, (2.19)

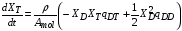, (2.20)

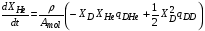, (2.21)

где 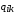– скорость соответствующей реакции. Скорости обеих реакций (2.16) и (2.17) считаются одинаковыми и равными 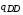. Величина 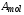определяется как 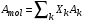, где индекс k относится к соответствующим атомам (ядрам) смеси.

Граничные условия задаются в следующем виде:

на оси симметрии, при 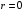ставятся условия нулевых градиентов

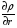u = 0, = 0, 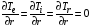, 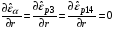; (2.22)

на внешней границе мишени, при 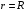ставятся условия

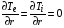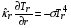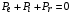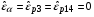, , ,. (2.23)

3. Результаты расчетов сжатия и горения мишени

3.1. Динамика сжатия мишени цилиндрическим пучком

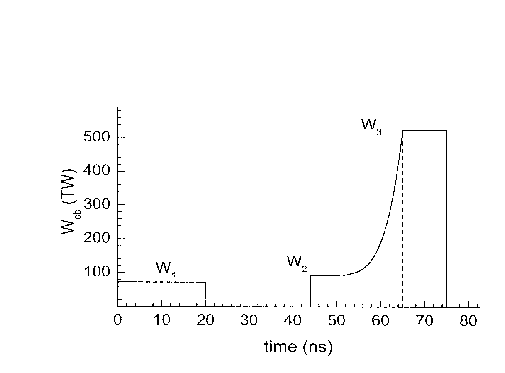
Облучение мишени производится вращающимся пучком однозарядных ионов ²⁰⁹Bi, как показано выше на Рис. 1. Оптимальное распределение полной мощности пучка по времени представлено на Рис. 3.

Рис. 3. Оптимизированная форма импульса мощности поджигающего пучка ²⁰⁹Bi ионов

Длительность импульса облучения составляет 75 нс. Полная энергия облучения равна 7,7 МДж. Форма импульса характеризуется изолированным низкоамплитудным пред-импульсом, необходимым для безударного нагружения материала мишени, и интенсивным ростом мощности на финальной стадии облучения.

Такая форма импульса обеспечивает минимальные диссипативные потери при сжатии смеси DT, а также минимальные потери энергии пучка при просветлении расширяющегося материала оболочки. Сжатие мишени завершается при t=94,7 нс. При этом достигается среднее значение плотности около 100 г/см³ и радиус DT шнура уменьшается до 50 мкм. В этот момент включается источник, обеспечивающий воспламенение DT-топлива, с полной энергией 1,7 МДж.

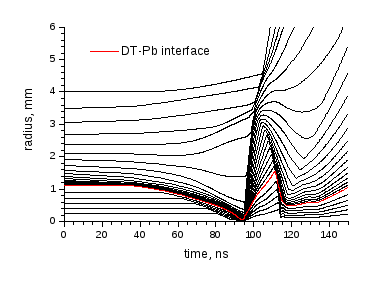Рис. 4. R,t диаграмма мишени на стадии сжатия и в начале разлета. В начальный момент радиус DT-топлива равен 1,12 мм, энерговложение сжимающего пучка происходит в области 1,25 ≤ r ≤ 2,50 мм в интервале

0 ≤ t ≤ 75 нс.

Описание и расчеты последующего разлета мишени в камере реактора требуют применения многомерных моделей или, по меньшей мере, использования одномерной сферической модели. В данной работе разлет мишени описывается в рамках одномерной сферической модели, в которой в качестве начальных данных используются распределения параметров в цилиндрической мишени в момент выхода ударной волны на поверхность. Математическая модель, используемая для расчета сферического разлета мишени, а также результаты расчетов описываются в параграфах 4, 5 и 6.

Расчетная динамика сжатия мишени показана на Рис. 4. Энерговложение профилировано по времени таким образом (Рис. 3), что топливо начинает сжиматься примерно через 40 нс после начала облучения, причем наиболее интенсивно этот процесс идет после 90 нс.

В момент 94,7 нс включается энерговложение поджигающего пучка, начинается термоядерное горение, и по мишени распространяется ударная волна, выходящая на поверхность примерно в момент 104 нс.

3.2. Выход ударной волны на поверхность мишени, генерация импульсов энергии нейтронов и рентгеновского излучения

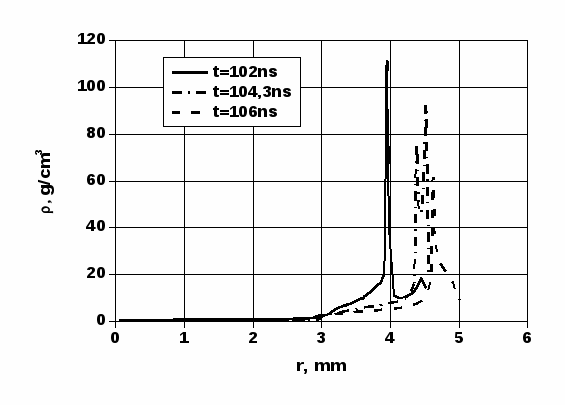
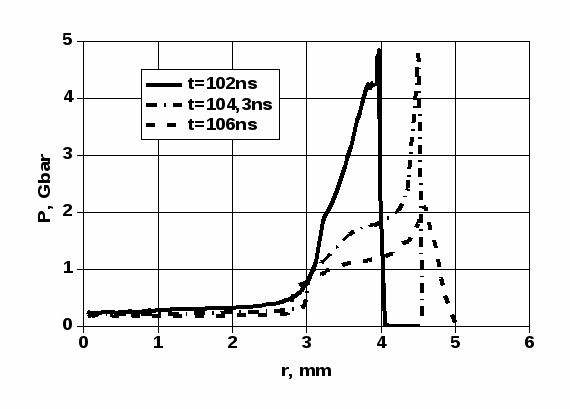
Процесс выхода ударной волны на поверхность мишени иллюстрируется распределениями гидродинамических переменных на Рис. 5-8 для трех моментов времени. Из радиальных распределений давления и скорости вещества в мишени (Рис. 5 и 6) можно видеть, что распространяющийся по оболочке динамический импульс имеет двухволновую структуру, состоящую из падающей и отраженной ударных волн. Отраженная от внешнего плотного слоя оболочки ударная волна, в которой происходит торможение среды, распространяется в направлении к оси мишени. Сжатие и нагрев вещества в этих ударных волнах представлены на Рис. 7 и 8. Падающая ударная волна чрезвычайно интенсивна. Пиковое давление на ее фронте достигает 5 Гбар. Соответственно в ней происходит 10-кратное увеличение плотности, что связано с высокой кратностью ионизации свинца за фронтом, 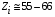. Температура ионов за фронтом ударной волны достигает значений 1 кэВ. Температура излучения близка к температуре ионов. На контактной поверхности температура ионов терпит скачок до 0,7 кэВ в DT-топливе.

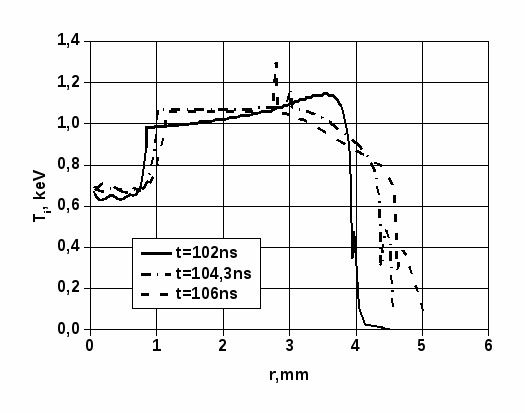
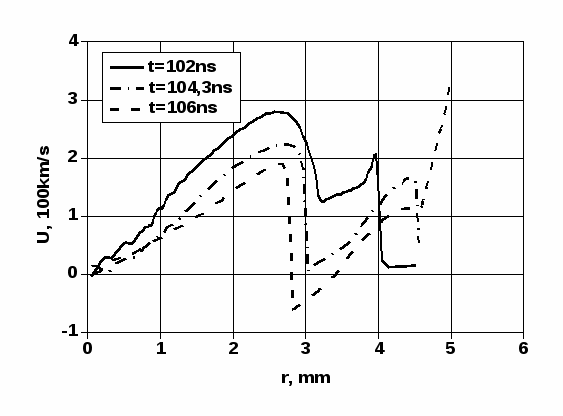
В численном расчете зафиксировать момент времени, когда ударная волна выходит на поверхность мишени, можно только приближенно. Эволюция профилей гидродинамических переменных указывает на то, что момент выхода ударной волны на поверхность приблизительно соответствует времени 104,3 нс. В следующий расчетный момент времени 106 нс профили гидродинамических переменных уже содержат участок разгрузки на отрезке 4,5 ≤ r ≤ 5,0 мм. На графике Рис. 6 видно, что в момент времени 102 нс скорость движения материала вблизи границы мишени остается значительно ниже (сплошная линия), чем в приближающемся к границе пике на расстоянии 4 мм от центра. Это означает, что ударная волна еще не вышла на поверхность мишени. В момент же 106 нс граница уже движется с высокой скоростью, тогда как в предыдущий расчетный момент 104,3 нс это движение только формируется.

Рис.5. Радиальные профили давления при выходе ударной волны

на поверхность цилиндрической мишени

Рис. 6. Радиальные профили скорости при выходе ударной волны

на поверхность цилиндрической мишени

Рис. 7. Радиальные профили плотности при выходе ударной волны

на поверхность цилиндрической мишени

Рис. 8. Радиальные профили температуры ионов при выходе ударной волны на поверхность цилиндрической мишени

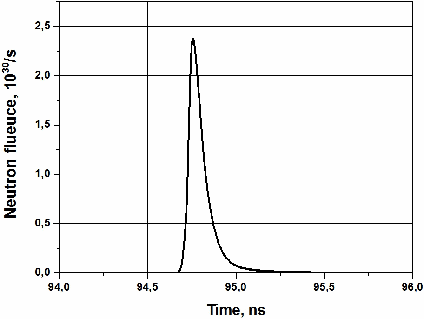
Основная часть термоядерной энергии при горении мишени выделяется в виде потока нейтронов, образующихся в реакции (2.15). Согласно расчетам, микровзрыв происходит на 95 наносекунде. Нейтронный импульс имеет полуширину 0,1 нс. Его временной профиль показан на Рис. 9.

Рис. 9. Зависимость от времени потока нейтронов 14 МэВ

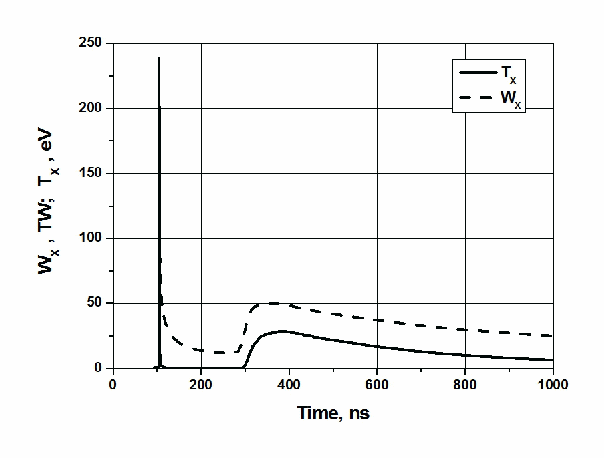
Рис. 10. Зависимость мощности и температуры рентгеновского

излучения на поверхности мишени от времени

Временная зависимость мощности рентгеновского излучения в процессе разгрузки мишени представлена на Рис. 10. На 104 наносекунде наблюдается острый пик рентгеновского излучения, вызванный приходом ударной волны на свободную поверхность мишени. Его полуширина составляет ~0,5 нс. Основной импульс рентгеновского излучения стартует с поверхности мишени на 300 наносекунде. Он имеет существенную продолжительность и относительно невысокую амплитуду ≈28 ТВт. Такая зависимость мощности рентгеновского излучения от времени обусловлена значительной массой оболочки мишени, и приводит к снижению термомеханической нагрузки на первую стенку реактора по сравнению с ИТС технологиями, использующими тонкие оболочки в мишенях.

4. Физико-математическая модель разлета мишени и испарения защитной жидкой пленки первой стенки камеры

4.1. Сценарий разлета мишени и испарения защитной пленки

При расчете динамики испарения защитной пленки под воздействием излучений, идущих из мишени, следует опираться на сценарий последовательности воздействий продуктов микровзрыва на стенку камеры. Важно учитывать, что продукты реакции достигают первой стенки за различное время.

Согласно результатам расчетов горения мишени, полученных по программе DEIRA-4 [11] в параграфе 3, первая стенка камеры реактора последовательно подвергается импульсным воздействиям различной физической природы и мощности.

Первым воздействием на жидкую пленку является короткий (0,5 нс) и мощный (240 ТВт) пред-импульс рентгеновского излучения, образующийся при выходе ударной волны на поверхность мишени (это происходит примерно через 9 нс после начала DT-реакции, см. Рис. 9 и 10). Через 13 нс после излучения пред-импульса с поверхности мишени он достигает первой стенки камеры, что происходит, таким образом, через 22 нс после микровзрыва. Следом за пред-импульсом через 77 нс после микровзрыва на стенку приходит поток нейтронов 14 МэВ, длительность которого равна времени эффективного горения мишени и составляет примерно 0,1 нс. Поток нейтронов 2,5 МэВ от DD-реакции приходит на стенку камеры через 182 нс после микровзрыва, но их доля в нагреве теплоносителя сравнительно мала, поэтому далее этим вкладом пренебрегаем. Основной рентгеновский импульс начинает воздействовать на жидкую пленку через 220 нс после микровзрыва.

Наибольший вклад в энерговыделение при горении DT-топлива вносят нейтроны с энергией 14 МэВ, для которых мишень практически прозрачна. Нагрев жидкой пленки нейтронами невелик вследствие большого пробега в свинце ~16см. Рентгеновское излучение, выходящее впоследствии с поверхности мишени, характеризуется планковским спектром, дилютированным за счет радиального распространения от взорвавшейся мишени. Собственно энергия, заключенная в мишени, определяется главным образом энергией альфа-частиц, возникших в ходе DT-реакции. Разлет мишени описывается системой уравнений гидродинамики с учетом энергии излучения. Это система уравнений двухтемпературной гидродинамики – с температурой вещества 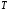и температурой излучения .

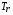Мишень на стадии разлета предполагается сферической и состоящей из свинца, для которого используется широкодиапазонное уравнение состояния А.Б. Медведева [12]. В камере в начальный момент времени находится пар теплоносителя с температурой первой стенки 823 K, создавая давление 0,01 Па. Начальным моментом для задачи о разлете является момент выхода ударной волны на поверхность мишени, которому отвечает момент времени 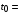104,3 нс (см. Рис. 5-8).

Отклик первой стенки камеры на микровзрыв определяется разогревом защитной пленки проходящим потоком нейтронов и ее абляцией под воздействием теплового излучения разлетающейся мишени.

При описании теплопроводности в жидкой пленке учитывается также электронная теплопроводность, согласно [13]. Для упрощения модели переноса тепла за счет нейтралов и электронов в работе применяется взвешенный коэффициент теплопроводности с весами, пропорциональными плотностям соответствующих компонент.

В разлетающейся мишени перенос теплового излучения описывается в диффузионном приближении с использованием данных [14] о росселандовых пробегах в плазме свинца с заданной температурой и плотностью.

Перенос рентгеновского излучения в атмосфере камеры моделируется на основе расчетных данных о его мощности и температуре на поверхности мишени, представленных на Рис. 10. Эти данные «переносятся» на первую стенку камеры с учетом дилютирования излучения в сферической геометрии и частичным его поглощением в атмосфере камеры. Для этого в уравнение энергии вещества вводится дополнительный источниковый член, определяющий плотность мощности поглощения излучения. Расчет глубины поглощения рентгеновского излучения в свинце основывается на спектральных данных лаборатории NIST [15].

Камера для простоты моделирования считается сферической. На границе жидкой пленки с первой стенкой камеры поддерживаются равновесные параметры. Считается также, что в начальный момент возмущения в атмосфере камеры и в защитной жидкой пленке отсутствуют, а все теплофизические параметры в пленке отвечают равновесному состоянию.

Таким образом, в данном разделе работы мишень в процессе своего разлета, атмосфера камеры и защитная пленка первой стенки описываются сквозным образом одной и той же системой уравнений. Это является новым шагом по сравнению с работами [4, 5].

Разлет мишени и перенос излучения в камере рассчитываются по самостоятельной программе, отличной от описанной выше модели DEIRA-4, которая поставляет данные начальных условий для задачи разлета. Мишень в гидродинамических расчетах считается сферической, как и камера, в которой происходит микровзрыв. Эти упрощения не принципиальны, поскольку характерный размер мишени (1 см) много меньше размера камеры (5 м), а излучение нейтронов и рентгеновских лучей можно считать изотропным.

Выпишем систему уравнений, описывающих поведение вещества в камере после микровзрыва. Они аналогичны системе уравнений (2.6)-(2.14), но отличаются от нее более упрощенной структурой. В этой системе, в частности, все вещество имеет одну температуру, так что электронные и ионные температуры совпадают.

4.2. Уравнения гидродинамики

Для описания процессов разлета мишени в камере и испарения защитной пленки первой стенки законы сохранения массы, импульса и энергии имеют вид [16, 17]

,

,

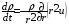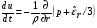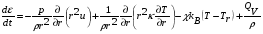, (4.1)

,

.

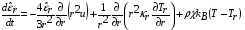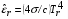Здесь 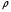– плотность, 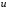– скорость, 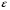– удельная внутренняя энергия вещества [Дж/кг], 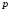– давление, 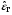– плотность энергии излучения [Дж/м³], 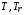– температуры соответственно вещества и излучения, 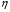– коэффициент вязкост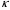и, и 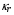– коэффициенты теплопроводности, 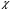– коэффициент температурной релаксации излучения и вещества, 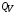– плотность энергии поглощения излучения в свинце. Обозначения универсальных постоянных: 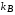– постоянная Больцмана, 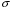– постоянная Стефана-Больцмана, 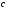– скорость света в вакууме.

4.3. Коэффициенты вязкости и теплопроводности

Коэффициент вязкости свинца в диапазоне 500-1000 К определяется по эмпирической зависимости [18]:

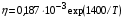. (4.2)

При 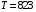К его значение равно 0,001 Па∙с. В отсутствие достоверных опытных данных при больших температурах вязкость положена равной нулю.

Коэффициент теплопроводности в веществе представляется в виде взвешенной суммы электронной и нейтральной компонент

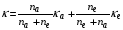, (4.3)

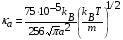, a = 1,8∙10^-10 [м],

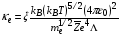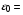, 8,85∙10^-12 [СИ],

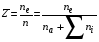, i=1,2,…,82,

где суммирование ведется по зарядовым состояниям иона свинца 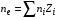, а параметр 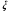слабо зависит от 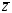(например, 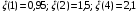). Кулоновский логарифм вычисляется по формул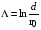е , где

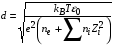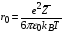, . (4.4)

Коэффициент радиационной теплопроводности определяется по формуле [13]:

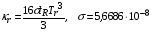[СИ]. (4.5)

Здесь 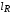есть средняя длина пробега по Росселанду:

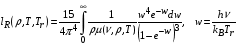, (4.6)

где 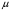– массовый коэффициент поглощения излучения в среде [см²/г], так что величина 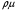имеет размерность обратной длины.

4.4. Коэффициенты поглощения и температурной релаксации

Релаксация между температурой электронов и температурой излучения описывается коэффициентом 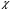в правой части (4.1). Этот коэффициент определяется в [11] по формуле

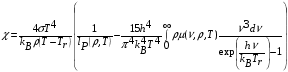, (4.7)

где средний планковский пробег 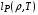определяется интегралом

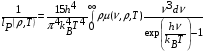. (4.8)

Таким образом,

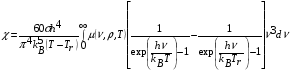. (4.9)

Формула (4.9) определяет 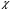как функцию плотности и двух температур – вещества и излучения. Однако двухтемпературная зависимость сильно усложняет процесс расчетов, поскольку для их проведения требуется табуляция 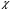путем численного интегрирования функционала (4.9) от эмпирической величины массового поглощения 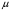. Будучи разложена в ряд по степеням 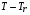, формула (4.9) в первом приближении дает независимость 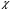от температуры излучения:

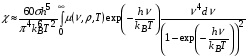. (4.10)

Таким образом, коэффициент релаксации приближенно можно записать в виде, аналогичном коэффициенту радиационной теплопроводности (4.5):

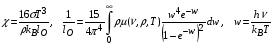. (4.11)

Нахождение величин 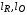связано с вычислением интегралов (4.6), (4.11), в которых спектральный коэффициент поглощения фотонов 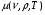в широкой области температур и плотностей для плазмы свинца был определен расчетным путем на основе программы THERMOS [14]. Указанные расчеты были проведены на основе релятивистской самосогласованной модели Хартри-Фока-Слэтера. В этой модели уровни энергий ионов и положения спектральных линий вычисляются в одноконфигурационном приближении Хартри-Фока. Вероятности различных состояний ионов определяются с использованием распределения Гиббса. В качестве профиля линий используется профиль Фойгта с учетом естественного уширения, уширения электронами, эффекта Штарка и эффекта Доплера, а также эффектов спин-орбитального расщепления методом Мошковского [19]. Расчет сечений фотоионизации проводится с использованием численных волновых функций электронов дискретного и непрерывного спектра, вычисленных в самосогласованном потенциале. При вычислении сечения тормозного поглощения используется модифицированная формула Борна-Эльверта с учетом эффектов вырождения. Комптоновское рассеяние вычисляется по уточненной формуле Клейна-Нишины.

Верификация программы THERMOS была проведена путем сопоставления с результатами расчетов по программам ведущих зарубежных центров – Ливерморской национальной лаборатории США (программы OPAL и HOPE), Лос-Аламосской национальной лаборатории США (программа LEDCOP), лаборатории Бер Шева из Израиля (программа STA). Проведены также сравнения с известными экспериментальными данными по измерению коэффициента прохождения (трансмиссии) для плазмы алюминия, железа, германия и гольмия [20]. Показано, что точность программы THERMOS при расчете детальных спектров достаточно высока. При расчете как детальных спектров, так и средних характеристик (в частности, усредненных по Плакнку и по Росселанду коэффициентов поглощения), получено хорошее согласие с наиболее продвинутыми зарубежными программами.

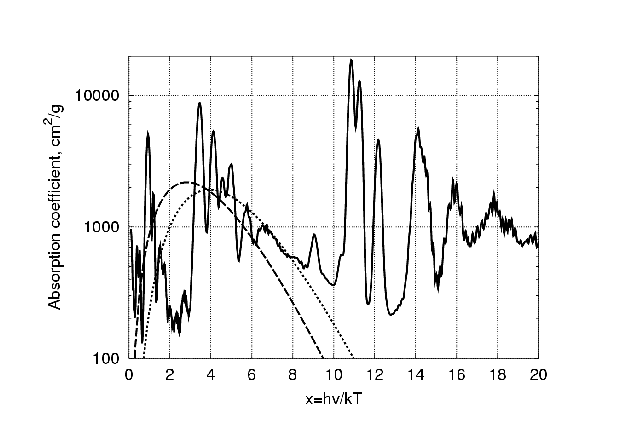
Пример расчетного коэффициента поглощения для плазмы свинца приведен на Рис. 11. Расчет проведен для температуры T=250 эВ и плотности ρ=10^-2 г/см³. Весовая функция Планка соответствует штриховой линии, а весовая функция для вычисления величины 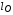обозначена пунктирной линией. Как видно из Рис. 11, использование весовой функции (4.11) смещает область влияния спектра поглощения в сторону больших энергий фотонов по сравнению с планковской весовой функцией (4.8).

Рис. 11. Коэффициент поглощения в плазме свинца 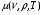при температуре T = 250 эВ и плотности ρ = 10^-2 г/см³ (сплошная линия)

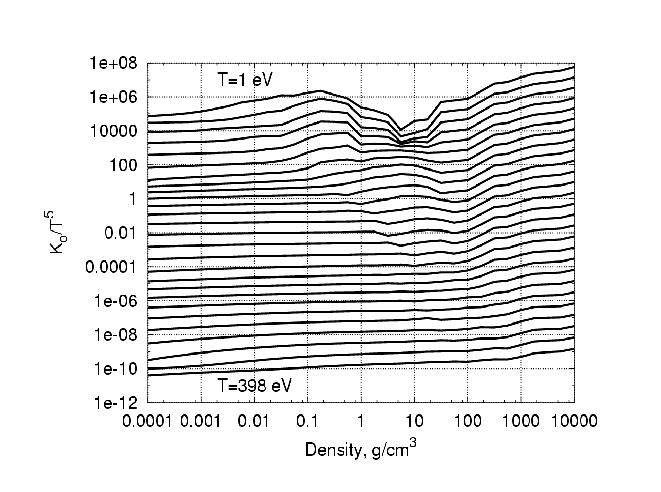
Усредненные с помощью весовой функции (4.11) величины 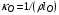в широкой области температур и плотностей представлены ниже на Рис. 12. Для удобства визуализации на графике представлены величины 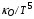. Характерная скейлинговая зависимость коэффициента 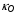от температуры и плотности среды в рассматриваемом диапазоне параметров приближенно может быть описана формулой  .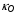

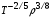Источниковый член в уравнении энергии (4.1) имеет вид 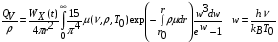. (4.12)

Здесь индексом 0 отмечены значения переменных на контактной поверхности между мишенью и атмосферой камеры. Контактная поверхность движется по траектории r₀(t). Значения параметров W_X(t) и Т₀(t) берутся из расчетов по программе DEIRA-4 (см. графики на Рис. 10).

Рис. 12. Изотермы коэффициента 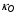в плазме свинца. Изотермы приведены с равномерным шагом по логарифму Т от 1 эВ до 398 эВ

4.5. Уравнение состояния

Широкодиапазонное уравнение состояния А.Б. Медведева [12] определяет зависимость 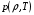неявным образом через подгоночный параметр – т.н. «объем коволюма» 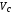. Само давление представляется в виде двух слагаемых – давления отталкивания 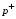и давления притяжения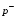

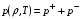, (4.13)

зависящих от 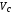. Ведем безразмерные величины 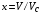, , 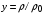где 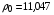г/см³ – некоторая постоянная, имеющая размерность плотности, своя для каждого вещества (в данном случае – для свинца). В модели [12] для свинца предложены следующие зависимости для определения 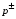[ГПа]:

- во всей области давлений ;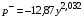

- при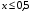

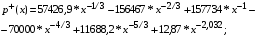
- в диапазоне 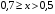применяется формула

;

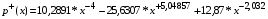- при .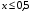

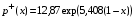Уравнение, которым определяется 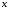, а, следовательно, по формулам, определенным выше, и давление 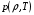, имеет вид:

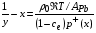. (4.14)

Здесь 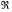– газовая постоянная, а 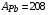– молярная масса свинца.

Система уравнений (4.13-4.14) показывает, что давление в модели в отсутствие ионизации определяется как функция температуры и плотности. По заданным значениям 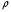и 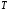из неявной зависимости (4.14) численно определяется значение виртуальной переменной 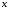, после чего по формуле (4.13) находится давление .

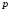С учетом ионизации в модель добавляется расчет концентрации ионов i-кратной ионизации 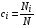, который проводится в предположении равновесия по формуле Саха:

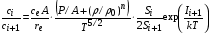, (4.15)

где 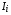– соответствующий потенциал ионизации свинца [13], 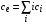, 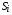– т.н. внутренняя статистическая сумма (в расчетах полагаем ), .

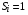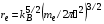Термическое уравнение состояния включает в себя энергию взаимодействия между частицами неидеальной среды, тепловую энергию и энергию ионизации:

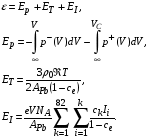(4.16)

4.6. Начальные и граничные условия для расчета разлета мишени и абляции жидкой пленки

Начальные условия при расчете разлета мишени отвечают условиям, которые сформировались в момент выхода ударной волны на поверхность мишени, т.е. в момент 104,3 нс.

1. Температура в начальный момент времени в атмосфере камеры и пленке 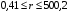[см] принята одинаковой и равной 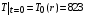К.

2. Плотность [г/см³] в соответствующих пространственных областях [см] принята однородной и равной

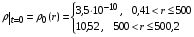
3. Давление в начальный момент времени определяется по заданным плотности и температуре согласно уравнению состояния.

4. Скорость в начальный момент в атмосфере и в пленке положена равной нулю: .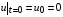

5. Начальные условия распределения плотности, давления, температуры и скорости в фаерболе определяются из данных по расчету сжатия и горения мишени (см. выше раздел 4.1 и Рис. 5-8). Однако при этом следует учесть, что численное решение по программе DEIRA-4 было получено для бесконечного цилиндра, тогда как далее рассматривается разлет конечной сферической мишени. Для пересчета данных с цилиндра на шар был использован следующий приближенный подход. Радиус шара определялся массой свинцовой мишени в пренебрежении массой DT, что дало 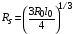= 4,25 мм, где 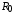, 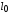- начальные радиус и длина мишени, указанные в параграфе 1. Объем шара был разбит на то же количество ячеек, что и при расчете горения цилиндрической мишени, причем цилиндрические и шаровые ячейки совпадали по массе. Это позволило провести пересчет шага сетки с цилиндра 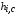на шар 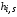по формулам:

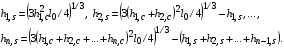
Сеточные значения функций плотности, температуры и т.д. были перенесены с цилиндрической на шаровую ячейку без изменений.

Граничные условия в камере и пленке:

1. В центре сферы приняты условия: .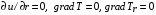

2. На границе «пленка/стенка» приняты условия .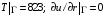

4.7. Алгоритм расчета и численная схема

Система уравнений гидродинамики (4.1) аппроксимировалась системой неявных разностных уравнений, обладающих свойством полной консервативности, согласно методике, описанной в [21], с использованием искусственной вязкости. Применительно к рассматриваемой задаче эта схема была подробно описана в нашей работе [22], поэтому разностные уравнения здесь для краткости не приводятся.

Система разностных уравнений решалась методом раздельных прогонок, применяемых последовательно для уравнения Навье-Стокса и уравнения непрерывности, уравнения эволюции внутренней энергии свинца, а также для уравнения лучистой теплопроводности. Полученные величины корректировались в процессе внешних итераций.

Совместно с уравнениями гидродинамики на каждом слое по времени и в каждой лагранжевой ячейке необходимо решать уравнения состояния (температурное и калорическое) и систему уравнений Саха. Однако, при реализации случая многократной ионизации (Z_Pb=82) совместное решение упомянутых выше систем уравнений в каждой лагранжевой ячейке на каждом временном слое требует заметных вычислительных ресурсов. Поэтому значения давления, степени ионизации и энергии ионизации были затабулированы в необходимых интервалах переменных (плотность, температура), а в процессе решения гидродинамических уравнений указанные величины находились методом интерполяции.

5. Результаты расчета разлета мишени и абляции жидкой пленки

5.1. Отклик жидкой пленки на воздействие рентгеновского пред-импульса и нейтронного потока

В настоящей работе совместный расчет разлета мишени и абляции жидкой пленки проводился от момента выхода ударной волны на свободную поверхность мишени до начала релаксации состояния атмосферы камеры после момента столкновения встречных фронтов.

Выход ударной волны на поверхность мишени порождает короткий, но мощный пред-импульс рентгеновского излучения. Одновременно начинается разлет мишени и последующие прогрев и сжатие атмосферы камеры. Защитная пленка первой стенки камеры реагирует на микровзрыв мишени, поглощая пред-импульс рентгеновского излучения и поток выходящих из мишени нейтронов. Расширение мишени сопровождается генерацией основного импульса рентгеновского излучения, начинающимся приблизительно 300-й наносекунде.

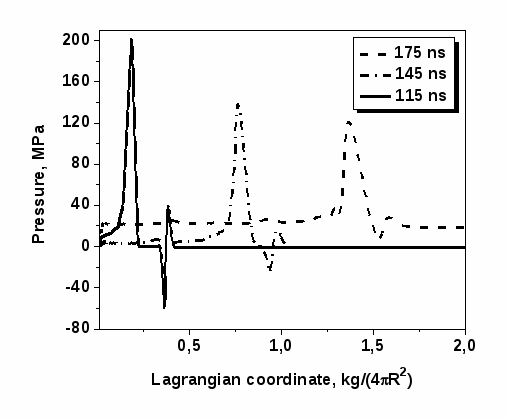
Ранее в работе [23] был рассчитано воздействие на пленку пред-импульса рентгеновского излучения и потока нейтронов. Расчет показал, что в жидкой пленке от пред-импульса возникает резкий пик давления – до 200 МПа (Рис. 13). При этом ударная волна распространяется по пленке, постепенно теряя амплитуду.

Рис. 13. Профили давления в лагранжевых координатах

(радиус камеры R=5 м) в жидкой защитной пленке от воздействий

пред-импульса рентгеновского излучения и потока нейтронов (время указано от момента включения облучения мишени тяжелоионным пучком).

На графике Рис. 13 видно плато на профиле давления на 175 наносекунде. Оно обусловлено почти мгновенным нагревом пленки на 11 градусов после прохождения потока нейтронов 14 МэВ, что приводит к повышению давления по всей толщине пленки примерно до 23 МПа. Основная часть потока нейтронов поглощается в толстом свинец-литиевом бланкете реактора (см. Рис. 2).

5.2. Разлет облака мишени и абляция жидкой пленки

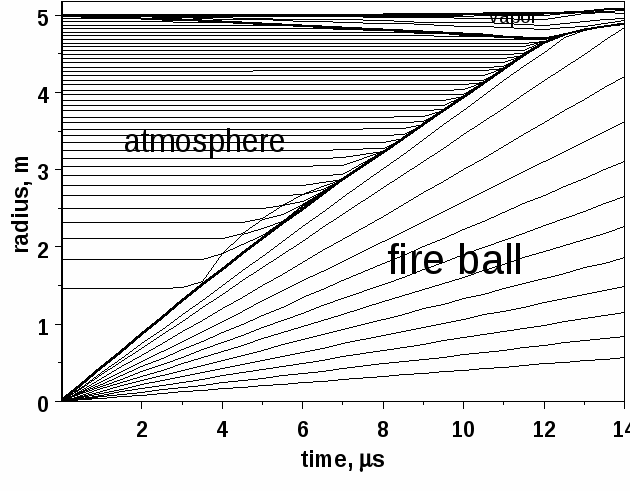
R,t диаграмма движения вещества в камере реактора приведена на Рис. 14. Как показал расчет, процесс разлета мишени (фаербола) и испарения защитной пленки первой стенки завершается столкновением двух фронтов примерно через 12 мкс после микровзрыва.

Рис. 14. R,t диаграмма движения вещества в камере реактора.

Диаграмма Рис. 14 предсталяет результат совместного расчета процессов разлета мишени, распространения ударной волны по атмосфере камеры и испарения внутрь камеры защитной жидкой пленки первой стенки. Видно, что столкновение двух встречных фронтов – фаербола и ионизованного пара – происходит приблизительно через 12 мкс после взрыва мишени на расстоянии около 40 см от стенки. После столкновения паровой слой нагревается до 10⁶ К, что вызывает доиспарение защитной пленки. Ионизованный пар теплоносителя продолжает расширяться внутрь камеры. Масса испаренного вещества перед столкновением двух фронтов составляет 1,5 кг. После доиспарения в камере единовременно находится около 10 кг испаренного вещества.

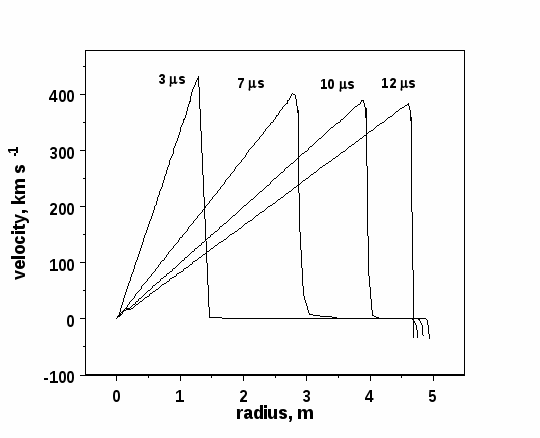
Распределение скорости в фаерболе практически линейное, его граница движется с почти постоянной скоростью порядка 400 км/с. В результате по атмосфере камеры распространяется ударная волна (Рис. 15). Поскольку масса атмосферы существенно меньше массы фаербола, траектории частиц атмосферы практически сливаются с линией фронта скачка давления.

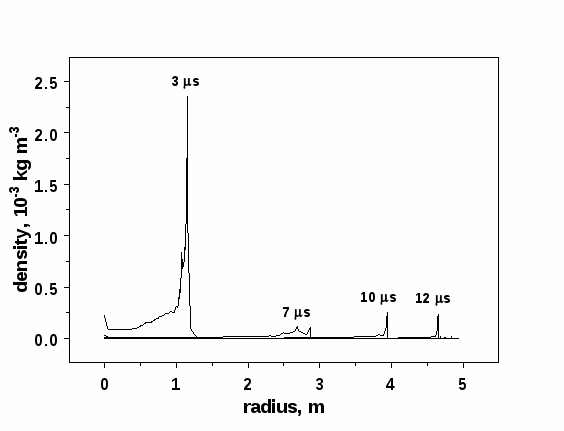
Радиальные распределения давления, скорости течения и плотности среды (фаербола, атмосферы камеры, пара), в различные моменты времени показаны на Рис. 15-17.

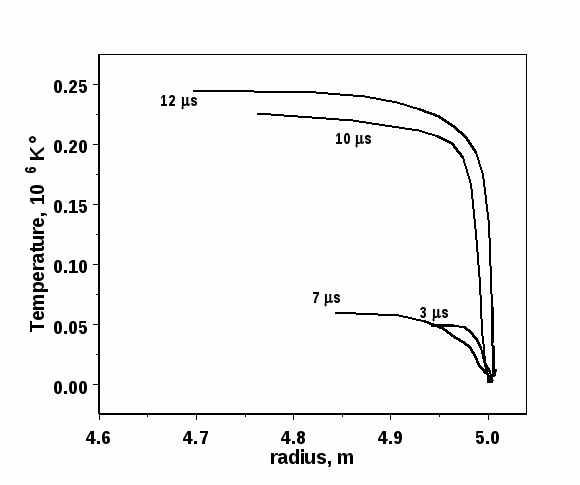
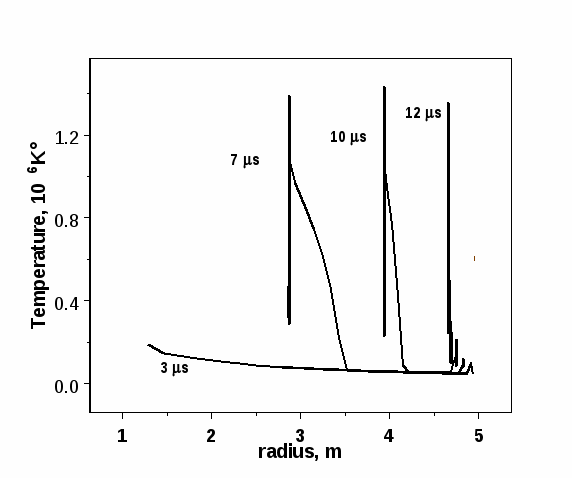
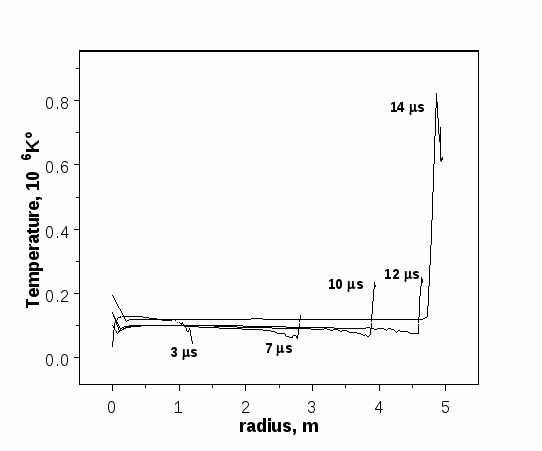
На Рис. 18-20 показано радиальное распределение температуры в фаерболе, атмосфере камеры и в испаренном слое защитной пленки в различные моменты времени.

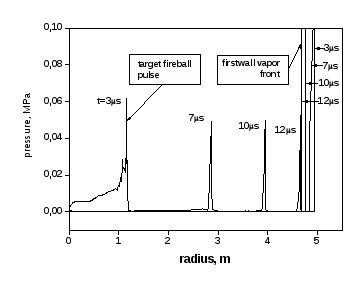
Рис. 15. Распределение давления в фаерболе, атмосфере камеры и паре

График Рис. 15 показывает встречное движение двух ударных волн. Слева направо по атмосфере камеры распространяется импульс давления от фаербола. Положение импульса показано через 3 мкс, 7 мкс, 10 мкс и 12 мкс (последнее – перед моментом столкновения фронтов). Эта ударная волна имеет высокую скорость движения (400 км/с, см. ниже Рис. 16), но вследствие интенсивного расширения вещества давление на фронте невелико – около 50 кПа (0,5 бар).

Справа налево движется фронт испаренного вещества. Скорость его движения 30 км/с примерно на порядок ниже скорости движения фронта фаербола, но плотность вещества в ионизованном паре высокая. В результате давление в паре на два порядка превосходит давление в фаерболе и составляет перед столкновением 5 МПа. На Рис. 15 для удобства восприятия линии фронтов давления в паровом слое «обрезаны» в их верхней части.

Рис. 16. Радиальное распределение скорости вещества в фаерболе и атмосфере.

Радиальные распределения скорости и плотности вещества фаербола в различные моменты времени представлены на графиках Рис. 16 и 17. Распределение скорости в файерболе практически линейно. Вещество атмосферы ускоряется в ударных волнах, возникающих в результате расширения фаербола и испаряющейся пленки. Максимальная плотность в импульсе, распространяющемся от центра камеры, падает от 10⁵ кг/м³ в момент выхода ударной волны на поверхность мишени до 10^-4 кг/м³ в момент столкновения встречных ударных волн вблизи стенки камеры.

Рис. 17. Распределение плотности вещества в фаерболе и атмосфере

Рис. 18. Распределение температуры в фаерболе

Графики распределения температуры в системе «фаербол-атмосфера-пар» показывают, что динамика изменения температуры в указанных составляющих различна. Фаербол (Рис. 18) при разлете расширяется и равномерно остывает. Некоторый рост температуры в последней расчетной ячейке фаербола, граничащей с атмосферой камеры, обусловлен сжатием в ней вещества и высоким давлением; эта ячейка отвечает положению фронта ударной волны, распространяющейся по атмосфере камеры.

Атмосфера (Рис. 19), в свою очередь, прогревается излучением, выходящим из фаербола и из примыкающих к нему слоев, которые сжимаются и имеют высокую температуру. Наблюдается отрыв температуры от фронта ударной волны за счет эффектов лучистой и электронной теплопроводности (см. [16, стр. 401, 410]). На прогрев области атмосферы перед фронтом ударной волны указывают характерные «брюшки» спадающих профилей температуры.

Рис. 19. Распределение температуры в атмосфере камеры

Рис. 20. Распределение температуры в испаренном слое жидкой пленки в различные моменты времени

Испаренный слой защитной жидкой пленки расширяется внутрь камеры, одновременно нагреваясь излучением, идущим из фаербола. На Рис. 20 видно, что с ростом времени «хвосты» ионизованного пара удаляются от первой стенки, одновременно с этим нагреваясь.

После столкновения двух фронтов температура и давление в соответствующей расчетной ячейке камеры резко возрастают. Важно, однако, что процесс релаксации, стимулированный доиспарением вещества жидкой пленки, приводит к весьма быстрому снижению температуры в этой ячейке в течение первых трех микросекунд после столкновения – примерно с темпом 100 тысяч градусов за микросекунду или 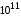К/с. В результате температура и давление в зоне столкновения снижаются, движение вещества к стенке камеры прекращается и начинается его равномерное размешивание по объему камеры.

Модель последующей релаксации атмосферы камеры была рассмотрена в работах [4-6]. В них было показано, что в течение приблизительно 0,02 с температура и плотность вещества в камере приходят к равновесному состоянию до взрыва.

6. Заключение

Моделирование полного сценария микровзрыва мишени и отклика камеры реактора на микровзрыв требует создания, по меньшей мере, двух различных гидродинамических кодов – одного для описания сжатия мишени, ее поджига и горения, и второго для описания разлета мишени, абляции первой стенки и взаимодействия встречных потоков вещества в камере. Это обусловлено принципиальным отличием физики процессов, протекающих на этих двух этапах, а также громадным отличием в них характерных масштабов времени, размеров, гидродинамических параметров и плотностей потоков массы импульса и энергии.

В данной работе моделирование микровзрыва мишени выполнено посредством последней версии кода DEIRA-4, а моделирование разлета мишени и отклика камеры реактора – с помощью вновь созданного кода радиационной гидродинамики. Сконструирована процедура сопряжения решений двух кодов с различной геометрией течения.

На основе кода DEIRA-4 осуществлен подбор энергетически эффективной мишени и режимных параметров тяжелоионных пучков, обеспечивающих требуемый уровень генерации термоядерной энергии в концепции ИТИС. Полностью определены временные профили потоков энергии, переносимых нейтронами, заряженными частицами и излучением в процессе микровзрыва, а также поля гидродинамических переменных в момент выхода ударной волны на свободную поверхность мишени.

В данной работе представлена модель и результаты численного сопряженного расчета разлета мишени в камере и воздействия продуктов термоядерного микровзрыва на первую стенку камеры реактора. Важность этой части работы заключается в том, что в ней впервые проведены численные расчеты отклика камеры реактора на микровзрыв в рамках одной программной реализации, позволяющей решать систему уравнений гидродинамики и переноса излучения не только для аномально высоких плотностей энергии (как непосредственно в фаерболе), но и для экстремальных условий (абляция жидкой пленки), а также в разреженной атмосфере камеры.

Благодарности

Авторы отмечают решающее влияние на эту работу академика В.И. Субботину, инициировавшему в Научном Совете РАН по физико-техническому анализу энергетических систем разработку концепции ИТИС. Авторы также глубоко благодарны члену-корреспонденту А.В. Забродину, руководившему работами по концепции ИТИС в ИПМ РАН, за поддержку и постоянное внимание к проводимым исследованиям.

Мы выражаем признательность академику В.П. Смирнову и члену-корреспонденту Б.Ю. Шаркову за многочисленные плодотворные обсуждения затрагиваемых вопросов. Мы также благодарим докторов физико-математических наук М.В. Масленникова и С.Л. Недосеева за критические замечания, полезные советы и ценные замечания по работе в ходе дискуссий на научных семинарах по проблемам ИТС.

Особую благодарность авторы выражают доктору физико-математических наук В.Г. Новикову за проведение расчетов коэффициента поглощения излучения в плазме свинца и релаксационного члена в однотемпературном приближении.

Литература

1. Medin S.A., Churazov M.D., Koshkarev D.G. et al. Evaluation of a power plant concept for fast ignition heavy ion fusion // Laser and Particle Beams, 2002. V.20, p.419–423.

2. Basko M. M., Churazov M. D., Aksenov A. G. Prospects of heavy ion fusion in cylindrical geometry. // Laser and Particle Beams, 2002. V.20, p.411–414.

3. Medin S.A., Churazov M.D., Koshkarev D.G., et al. Reactor Chamber and Balance-of-Plant Characteristics for Fast-Ignition Heavy-Ion Fusion Power Plant // Fusion Science and Technology, 2003. V.43, No.3, p.437–446.

4. Медин С.А., Орлов Ю.Н., Суслин В.М., Паршиков А.Н. Моделирование отклика первой стенки камеры и бланкета реактора ИТС на микровзрыв. / Препринт ИПМ им. М.В. Келдыша РАН, № 41, 2004.

5. Медин С.А., Орлов Ю.Н. Концепция камеры реактора ИТС на тяжелых ионах // ВАНТ, сер. Термоядерный синтез, 2005. Вып. 2. С. 3-14.

6. Medin S.A., Basko M.M., Koshkarev D.G., Orlov Yu.N., Parshikov A.N., Sharkov B.Yu., Suslin V.M. Power Plant Design and Accelerator Technology for Heavy Ion Inertial Fusion Energy // Nuclear Fusion, 2005. V. 45. S291-S297.

7. Koshkarev D.G. Charge-Symmetric Driver for Heavy-Ion Fusion. // IL Nuovo Chimento, 1993. Vol.106 A, No.11, p.1567–1571.

8. Кошкарев Д.Г., Чуразов М.Д., Баско М.М. и др. Мощный тяжелоионный драйвер для зажигания термоядерной ДТ мишени. / Препринт ИТЭФ, 4-01, 2001.

9. Чуразов M.Д., Аксенов A.Г., Забродина E.A. Зажигание термоядерных мишеней пучком тяжелых ионов. // ВАНТ, Сер. Математические модели физических процессов, 2001. Вып. 1, №.20, с.1–13.

10. Долголева Г.В., Забродин А.В. Кумуляция энергии в слоистых системах и реализация безударного сжатия. М.: Физматлит, 2004, 70 с.

11. Basko M.M. DEIRA 1D-3T hydrodynamic code for simulating ICF targets driven by fast ion beams. / Moscow: ITEP, 2001.

12. Медведев А.Б. Модификация модели Ван-дер-Ваальса для плотных состояний. / В сб.: Ударные волны и экстремальные состояния вещества. Под ред. В.Е. Фортова, Л.В. Альтшулера, Р.Ф. Трунина и А.И. Фунтикова. М.: Наука, 2000.

13. Силин В.П. Введение в кинетическую теорию газов. М.: Наука, 1971.

14. Никифоров А.Ф., Новиков В.Г., Уваров В.Б. Квантово-статистические модели высокотемпературной плазмы и методы расчета росселандовых пробегов и уравнений состояния. М.: Физматлит, 2000.

15. Hubbell J.H., Seltzer S.M. Tables of X-Ray Mass Attenuation Coefficients. NIST, 1996.

16. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука, 1966.

17. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика VI. Гидродинамика. М.: Наука, 1988.

18. dai Kai Sze, Ralph Moir, Steve Zinkle. Data Base for Liquid Breeders and Coolants. / APEX Interim Report, November, 1999.

19. Драгалов В.В., Никифоров А.Ф., Новиков В.Г., Уваров В.Б., Статистический метод расчета поглощения фотонов в плотной высокотемпературной плазме, Физика плазмы, 1990, т.16, № 1, с.77-85.

20. Новиков В.Г., Никифоров А.Ф., Уваров В.Б., Драгалов В.В. Поглощение фотонов в высокотемпературной плазме. / Препринт ИПМ им. М.В. Келдыша РАН, № 17, 1992. – 22 с.

21. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М.: Наука, 1980.

22. Медин С.А., Орлов Ю.Н., Суслин В.М. Расчет динамики испарения защитной пленки первой стенки камеры реактора ИТС / Препринт ИПМ им. М.В. Келдыша РАН, № 62, 2004. – 28 с.

23. S.A. Medin, M.M. Basko, Yu.N. Orlov and V.M. Suslin. X-ray and Ion Debris Impact on the First Wetted Wall of IFE Reactor. / 33-d European Physical Society Conference on Plasma Physics. Roma, Italy, June 19-23, 2006. Collected abstracts, p.32.