МБОУ СОШ№49г .Шахты

Ростовской области

План-конспект урока алгебры

в 9 классе

на тему:

«Графики функций y=ах²+n и y=а(х-m)²»

Разработала:

учитель математики

1 категории

Гладкая Наталья Викторовна

2013 – 2014 учебный год

Цель урока:

1. Научить изображать схематически графики функций y= ах²+n и y=а(х-m)² с помощью параллельного переноса вдоль осей координат.

2. Строить с помощью шаблона графики функций.

3. Развивать интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание.

Планируемые результаты:

В ходе урока учащиеся

- развивают умения

• систематизировать знания о графиках функций, их свойствах;

• устанавливать соответствие между графиком и формулой;

• делать обобщения и выводы.

Тип урока: урок «открытия» новых знаний.

Формы работы: фронтальная, парная, индивидуальная.

Методы:

По источникам знаний: словесные, наглядные;

По степени взаимодействия учитель-ученик: эвристическая беседа;

Относительно характера познавательной деятельности: репродуктивный, частично-поисковый.

Оборудование:

• компьютер

• экран

• мультимедийный проектор

• раздаточный материал.

Ход урока

1) Организация начала урока

Здравствуйте, ребята! Сегодня на уроке мы расширим сведения о свойствах квадратичной функции, а так же познакомимся с графиками частных видов квадратичной функции: у = ах², у = ах² + n, y = a (x – m)²; у=a (x – m)² +n.

Начать урок мне хотелось бы с китайской пословицы, которая гласит:

«Я слушаю, – я забываю;

Я вижу, – я запоминаю;

Я делаю, – я усваиваю» (Слайд 2)

Я желаю вам успешной работы на уроке!

2) Актуализация знаний учащихся.

• Функция какого вида, называется квадратичной?

• Что является графиком квадратичной функции?

• От чего зависит направление ветвей параболы?

Посмотрите на график функции у =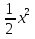 и перечислите его свойства? (Слайд 3)

3) Изучение нового материала.

Сейчас я предлагаю вам разделиться на 3 группы. Каждой группе предоставляется задание и по истечению времени вы должны показать результаты работы и сделать выводы. В своей работе вы можете пользоваться учебником.

Задание. Построить графики функций в одной системе координат и сделать выводы об их расположении.

1 группа: у=х², , у=х²+1, у= х²-1 (Учебник: стр. 35)

2 группа: у=х², у=(х+1)², у=(х-1)² (Учебник: стр. 37)

3 группа: у=х², у=(х+1)² + 2, у=(х-1)² – 2. (для более подготовленных учащихся) (Учебник: стр. 38) (Слайд 4, 5, 6 для проверки работы групп)

Итак, ребята, я предлагаю вам обобщить полученные сведения и заполнить письменно таблицу. (Учитель готовит таблицу для каждого учащегося и по мере защиты своей работы другими группами, ребята заполняют её как памятку для себя) (Слайд 7-9)

f(x + n)

n > 0

Схематический график

n < 0

Схематический график

Сдвиг влево вдоль оси ОХ на n единиц

Сдвиг вправо вдоль оси ОХ на n единиц

f(x ) + m

m > 0

m < 0

Сдвиг вверх вдоль оси ОУ на m единиц

Сдвиг вниз вдоль оси ОУ на m единиц

f(x + n) + m

n > 0, m > 0

n < 0, m < 0

Сдвиг влево вдоль оси ОХ на n единиц, затем сдвиг вверх вдоль оси ОУ на m единиц

Сдвиг вправо вдоль оси ОХ на n единиц, затем сдвиг вниз вдоль оси ОУ на m единиц

n > 0, m < 0

n < 0, m > 0

Сдвиг влево вдоль оси ОХ на n единиц, затем сдвиг вниз вдоль оси ОУ на m единиц

Сдвиг вправо вдоль оси ОХ на n единиц, затем сдвиг вверх вдоль оси ОУ на m единиц

4) Закрепление полученных знаний.

Первичное закрепление.

Устно.

Задания на соотнесения.

1. Какому графику соответствует функция, заданная формулой y = x² – 2? (Слайд 10 )

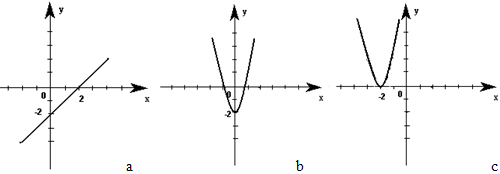
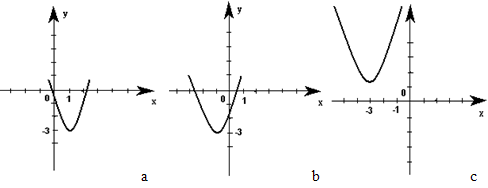
2. Функция задана формулой. Соотнесите график функции с её формулой заполнив таблицу.

1) у = 2(х + 1)² - 3 2) у = 2(х + 3)² + 1 у = 2(х - 1)² - 3.

1

2

3

b

c

a

(Слайд 11)

3. Укажите график функции, соотнеся их с формулой, и прочитай полученное слово:

1) y = –x²;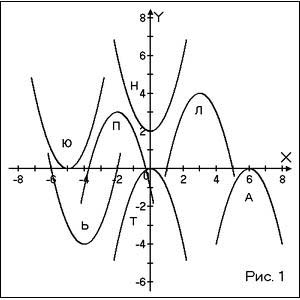

2) y = (x+5)²;

3) y = –(x–3)²+4;

4) y = (x+4)²–4;

5) y = –(x+2)²+3;

6) y = –(x–6)²;

7) y = x²+2.

т

ю

л

ь

п

а

н

(Слайд 12)

Физминутка (Слайд 13)

Робот делает зарядку

И считает по порядку.

Раз – контакты не искрят, (Движение руками в сторону.)

Два – суставы не скрипят, (Движение руками вверх)

Три – прозрачен объектив (Движение руками вниз.)

И исправен и красив. (Опускают руки вдоль туловища.)

-Ребята, посмотрите в природе тоже можно встретить объекты имеющие параболическую форму. (Слайд 14)

Вторичное закрепление.

Письменно

1. С помощью шаблона параболы постройте в координатной плоскости графики функций.

(Слайд 15, 16)

y= 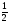x²; y=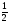x²+2; y=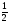x² – 3; y= - 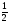x²; y= - 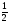x² – 3;

y=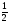(x – 4)²; y=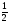(x+3)²; y=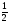(x – 1)²+2; y= - 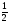(x+1)² – 3. (Работа в парах)

5) Самостоятельная работа (Слайд 17)

Используя шаблоны парабол y=2x²; y=3x², постройте графики функций.

I. Вариант II. Вариант

1. y = 2x² 1. y = 3x²

2. y = 2 (x-2)²+1 2. y = 3 (x-2)²+1

3. y = -2 (x-2)² 3. y = 3(x-3)²-3

4. y = 2 (x+4)² -2 4. y = -3(x-4)²+2

5. y = -2 (x-5)²+3 5. y = -3(x-5)²-1

6) Рефлексия. Итог урока. (слайд 18)

Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:

1. сегодня я узнал…

2. было интересно…

3. было трудно…

4. я выполнял задания…

5. я понял, что…

6. теперь я могу…

7. я почувствовал, что…

8. я приобрел…

9. я научился…

10. у меня получилось …

11. я смог…

12. я попробую…

13. меня удивило…

14. урок дал мне для жизни…

15. мне захотелось…

8) Домашнее задание.

Индивидуальные карточки.

Интернет источники.

• Физминутка, картинка робота. http://ree-ikt.blogspot.ru/p/blog-page_3066.html

• Яндекс картинки. http://images.yandex.ru/yandsearch?text=%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%BF%D0%B0%D1%80%D0%B0%D0%B1%D0%BE%D0%BB%D1%8B%20%D0%B2%20%D0%BF%D1%80%D0%B8%D1%80%D0%BE%D0%B4%D0%B5&img_url=http%3A%2F%2Fimg-fotki.yandex.ru%2Fget%2F4009%2Fshef007.33%2F0_186a7_e56a6f9a_L.jpg&pos=3&rpt=simage&lr=39&noreask=1&source=wiz

• Рефлексия http://nsportal.ru/nachalnaya-shkola/raznoe/vidy-refleksii