МОУ «Ангоянская средняя общеобразовательная школа»

Открытый урок

по алгебре и началам анализа

10 класс

Тема: Методы решения тригонометрических уравнений

Учитель высшей квалификационной категории

Золтуева Марина Владимировна

Тема: Методы решения тригонометрических уравнений

Метод решения хорош, если с самого начала мы можем предвидеть – и впоследствии подтвердить это, - что, следуя этому методу, мы достигаем цели.

Лейбниц

Цели урока:

Образовательные: систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения тригонометрических уравнений.

Развивающие: содействовать развитию качеств, лежащих в основе познавательных способностей: мышление, память, внимание, воображение, речь.

Воспитывающие: побуждать учеников к преодолению трудностей в процессе умственной деятельности, воспитывать упорство и трудолюбие, укреплять интерес к математике.

Валеологические: создать комфортную обстановку на уроке для учащихся всех уровней обучения, исключить перегрузку детей.

Оборудование: экран, кодоскоп, набор карточек для сбора схемы на магнитной доске, показывающей связь между решениями и коэффициентами уравнения

а∙sinx + b∙cosx = 1, таблица со списком уравнений, карточки с тестовым заданием, копировальная бумага, табло результативности

План урока

1. Организационный момент (2 мин.)

2. Разминка (6 мин.)

3. Решение уравнений (12 мин.)

4. Тестирование (7 мин.)

5. Демонстрация методов решения уравнений (15 мин.)

6. Домашнее задание (1 мин.)

7. Итог урока (2 мин.)

Ход урока

I.Организационный момент (Вводная беседа)

Сегодня мы поговорим о методах решения тригонометрических уравнений. Знаем, что правильно выбранный метод часто позволяет существенно упростить решение, поэтому все изученные нами методы всегда нужно держать во внимании, чтобы решать конкретные задачи наиболее рациональным из них.

II. Разминка

Учащимся предлагается провести классификацию тригонометрических уравнений по методам решения.

Задание. Рядом с каждым уравнением 1-12 указать номер метода, которым можно решить данное уравнение наиболее рационально.

Классификация тригонометрических уравнений по методам решения.

№

Уравнения

№ метода

Методы

1

sin x/3 – cos 6x = 2

4(б)

1.Разложение на множители.

2.Введение новой переменной:

а) сведение к квадратному;

б) универсальная подстановка;

в) введение вспомогательного аргумента;

3.Сведение к однородному уравнению.

4.Использование свойств функций, входящих в уравнение:

а) обращение к условию равенства тригонометрических функций;

б) использование свойства ограниченности функции

2

|1- cos x | _{· sin x = 4sin}²_{x·cos x}

1 – cos x

1

3

_{√ 3·sin x -} |1+ cos x | _·sin²_{x = sin}²_x

1 + cos x

1

4

5sin x – 2cos x = 1

3, 2(б,в)

5

sin 3x·cos 2x = 1

4(б)

6

cos2x = √2 (cos x – sin x)

1,2(б,в),3

7

1 - sin 2x = cos x – sin x

1,2(б,в),3

8

cos 3x = sin x

4(а)

9

4 – cos²x = 4sin x

2(а)

10

sin 3x – sin 5x = 0

4(б)

11

tg 3x · tg (5x + П/3) = 1

4(а)

12

2 tg x/2 – cos x = 2

1,2(а,б,в), 3, 4(а)

Обсуждение проводится в быстром темпе и выясняется, что наибольшее количество методов можно применить при решении уравнения №12. Отмечается, что первые три из указанных методов являются традиционными для решения тригонометрических уравнений. Что касается последнего метода, то он рассматривается достаточно редко. Предлагается остановиться на этом методе.

III. Решение уравнений

Метод использования свойства ограниченности функции (кодопозитив 1)

Если функции f(x) и g(x) таковы, что для всех x выполняются неравенства

f(x) ≤ а и g(x)≤ в, и дано уравнение f(x) + g(x) = а + в, то оно равносильно системе

f(x) = а

g(x) = в

Ученики-консультанты выполняют решение с объяснением у доски, остальные – в тетради.

Уравнение №1. sin x/3 – cos 6x = 2

Решение. Поскольку | sin x/3 | ≤ 1 и | cos 6x | ≤ 1, имеем систему

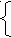
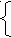
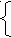sin x/3 = 1 x/3 = П/2 + 2Пк ,кcZ x = 3П/2 +6Пк, кcZ

cos 6x = -1 6x = П+2Пп,псZ x = П/6 =Пп/3, псZ

Покажем общее решение на тригонометрической окружности. Решение первого уравнения системы обозначим *, а второго точкой и найдём их общее решение.

П/2

5П/6 П/6

7П/6 11П/6

3 П/2

Ответ: x = 3П/2 + 6Пr,rcZ

Метод использования условия равенства одноимённых тригонометрических функций (кодопозитив 2)

sin f(x)=sin g(x)

f(x) = g(x)+2Пk ,kcZ

f(x) =П - g(x)+2Пn ,ncZ

cos f(x)= cos g(x)

f(x) = g(x)+2Пk, kcZ

f(x) = - g(x)+2Пn ,ncZ

tg f(x)=tg g(x)

f(x) = g(x)+Пk ,kcZ

g(x) =П/2+Пr ,rcZ

Трое учеников решают уравнения № 8,10,11 на доске, остальные учащиеся решают любой из этих номеров в тетради.

Уравнение № 10. sin 3x – sin 5x = 0

Решение. На основании условий равенства двух синусов имеем:

5x = 3x+2Пk ,kcZ 2x = 2Пk ,kcZ x = Пk ,kcZ

5x =П - 3x+2Пn ,ncZ 8x = (2п +1)П ,ncZ x = (2п +1)П/8 , ncZ

Ответ: x = Пk ,kcZ ; x = (2п +1)П/8 , ncZ

Уравнение №8. cos 3x = sin x

Решение. cos 3x = cos (П/2 - x).

Воспользуемся равенством косинусов двух углов, имеем:

3x- (П/2 - x) = 2Пk, kcZ 4x = (4п+1)П/2, ncZ x = (4п+1)П/8, ncZ

3x+ (П/2 - x) = 2Пn ,ncZ 2x = (4к-1)П/2, кcZ x = (4п-1)П/4, кcZ

Ответ: x = (4п+1)П/8, ncZ; x = (4п-1)П/4, кcZ

Уравнение № 11. tg 3x · tg (5x + П/3) = 1

Решение: Делим обе части уравнения на tg 3x. Это допустимо, т. к. в данных условиях tg 3x не может быть равно нулю:

tg (5x + П/3) = 1 , tg (5x + П/3) = сtg 3x, tg (5x + П/3) = tg ( П/2 – 3х)

tg 3x

На основании условия равенства тангенсов двух углов имеем:

5x + П/3 - П/2 + 3х = Пn

8х = П/6+Пn, х = (6п + 1) П/48, ncZ

При каждом значении х из этой совокупности каждая из частей уравнения

tg (5x + П/3) = tg ( П/2 – 3х) существует.

Ответ: (6п + 1) П/48, ncZ

IV. Тестирование

Метод сведения уравнения вида а sin х + в соs х = с (а,в,с ≠ 0) к однородному уравнению.

Выясняем преимущества данного метода над основными способами решения этого уравнения (введение вспомогательного угла, применение формул универсальной под­становки). Отмечаем, что он, так же как и метод рационализации, применяется в физике при сложении гармонических колебаний.

На магнитной доске ученик составляет системно-обобщающую таблицу, раскрывающую идею решения уравнения вида а sin х + в соs х = с (а,в,с ≠ 0), из заранее подготовленных карточек.

Условия на коэффициенты

Решения

x = 2arctg a +(-) √ Δ + 2Пn ,ncZ

b + c

Δ > 0

D > 0

D > 0

b + c ≠ 0

x = 2arctg a + 2Пn ,ncZ

b + c

Δ = 0

решений нет

Δ < 0

b + c = 0

x= П(1 +2n) ,ncZ

x = - 2arctg b + 2Пk ,kcZ

a

Знания остальных учащихся проверяются тестом с последующим ­контролем.

Тест. Раскройте идею решения уравнения вида а sin х + в cos х = с (а,в.с ≠ 0), показав стрелками зависимость решений от условий, наложенных на коэффициенты.

b + c = 0

b + c ≠ 0

1.

4sin х - 5cos х =5

2.

3sin х+4cos х =5

3.

5sin х + 4cos х =5

4.

- sin х + cos х =12

Δ = 0

Δ < 0

Δ > 0

x= П(1 +2n) ,ncZ

x = -2arctg b + 2Пk ,

а

kcZ

x = 2arctg a +

b + c

+ 2Пn , ncZ

Нет

реше

ния

x = 2arctg a +(-)√ Δ +

b + c

+ 2Пn , ncZ

Выполнил:___________ Оценка:________

V. Демонстрация методов решения уравнения

(индивидуальное домашнее задание)

Отмечаем, что в уравнении а sin х + в соsх = с а, в и с - любые действительные числа. Если а = b = 0, а с ≠ 0, то уравнение теряет смысл;

Если а = в = с = 0, то х - любое действительное число, т. е. уравнение обращается в тождество.

Уравнение sin х + cos х = 1 можно решать, по крайней мере, ше­стью способами.

На доске 6 учеников показывают различные способы реше­ния этого уравнения. Проводим сравнительный анализ и коммента­рий решений.

Способ 1. Сведение к однородному уравнению.

- Выразим sin х, cos x и 1 через функции половинного аргумента:

Способ 2. Преобразование суммы в произведение.

Способ 3. Введение вспомогательного угла.

- Разделим обе части уравнения на √2:

Способ 4. Метод рационализации (кодопозитив 3)

Введение выражений для sin x и cos x через tg x/2 по формулам

Обращение к функции tg x/2 предполагает, что cos x/2 ≠ 0, т.е. х ≠ 2Пn ,ncZ

Такой способ решения получил название - метод рационализации, т. к. вспомогательное неизвестное вводится так, чтобы после подстановки получилось рациональное уравнение относительно этого вспо­могательного неизвестного.

Итак, по формулам исходное уравнение примет вид:

Способ 5. Замена cos x выражением + √ 1 – sin² x:

Способ 6. Применение формулы sin x +cos x = √2 sin (x + П/4)

Исходное уравнение примет вид:

- Все решения показываем на триго­нометрическом круге цветными точками, отмечаем их совпадение.

VI. Домашнее задание

Решить уравнение №12 из таблицы несколькими способами

VII. Итог урока

Учитель подводит итоги урока, выставляет оценки, даёт пояснения к домашнему заданию