УРОК АЛГЕБРЫ В 8 КЛАССЕ ПО ТЕМЕ: «ТЕОРЕМА ВИЕТА»
МОУ «ООШ п.Чапаевский Пугачёвского района Саратовской области»
«Поэтом по праву должна быть воспета
О свойствах корней теорема Виета...»
УРОК АЛГЕБРЫ В 8 КЛАССЕ
ПО ТЕМЕ:
«ТЕОРЕМА ВИЕТА»
Учитель
Конева Наталья Николаевна
2011 г.
Урок по теме «Теорема Виета» (2 часа)
Цели урока:
«открыть» зависимость между корнями и коэффициентами приведённого квадратного уравнения;
вместе с учащимися установить зависимость между корнями и коэффициентами уравнения общего вида;
учить применять теорему Виета и обратную ей теорему при решении квадратных уравнений в различных ситуациях и при решении задач разной степени трудности;
развивать интерес к математике, показав на примере жизни Виета, что математика может быть увлечением.
Оборудование.
Оформленная доска. Таблица. Мультимедиапроектор.
Карточки с заданиями. Портрет Франсуа Виета.
ХОД УРОКА
1. Проверка домашнего задания и постановка проблемы.
Учитель. Дома вы должны были решить квадратные уравнения. Давайте проверим, как вы справились с этим заданием. В таблицу, заранее заготовленную на доске, внесём корни для каждого уравнения, которые вы решали самостоятельно.
уравнение
корни
Произведение корней
Сумма корней
х2-2х -15=0
5 и-3
-15
2
х2 +3х - 28=0
4 и-7
-28
-3
х2 - 14х+28 =0
6 и 8
48
14
х2+15х + 36=0
-12 и -3
36
-15
2х2 +5х – 3 = 0
1/2 и-3
-3/2
-5/2
3х2 - х – 2 = 0
-2/3 и 1
-2/3
1/3
х2+рх +q =0
![]()
g
-р
ах2 + вх + с =0
![]()
с/а
-в/а
Открытие новых знаний.
Учитель. Сравните сумму и произведение корней приведённых квадратных уравнений с коэффициентами уравнения. Какая существует зависимость? Какое предположение можно сделать? Сформулируйте утверждение и заполните предпоследнюю строку таблицы.
Вывод (учащиеся делают самостоятельно)
Слайд 1 Слайд 2
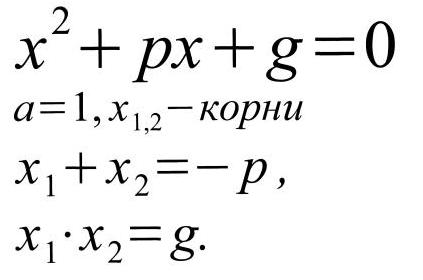

Учитель. Таким образом мы сформулировали с вами теорему Виета для приведённого квадратного уравнения. Доказали мы её? Нет. Мы увидели закономерность на примерах. Так как все примеры рассмотреть невозможно, это не является доказательством.
Докажем теорему.
Дано: х2 + рх + q =0,где а = 1, х1 и х2 -корни квадратного уравнения.
Доказать: х1 + х2 = -р; х1 ∙ х2 = q .
Доказательство: 1. Так как по условию уравнение имеет два корня, то
![]()
![]()
![]()
Теорема доказана.
Вернёмся к уравнениям в таблице, у которых первый коэффициент не равен 1.
Сравним произведение корней и сумму корней с коэффициентами. Сделаем вывод. Запишем его в таблицу. Сформулируйте теорему Виета для произвольного квадратного уравнения.
Слайд 3
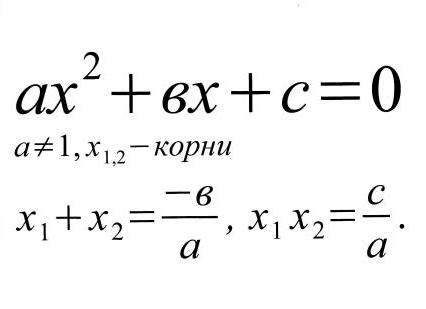 Чтобы лучше её запомнить, можно выучить стихотворение: «Теорема Виета»
Чтобы лучше её запомнить, можно выучить стихотворение: «Теорема Виета»
Поэтом по праву должна быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого-
Умножишь ты корни и дробь уж готова:
В числителе с, в знаменателе а
И сумма корней тоже дроби равна,
Хоть с минусом дробь та, но что за беда:
В числителе в, в знаменателе а.
 Слайд 4 3.Историческая справка. (готовится учащимися, как дополнительное домашнее задание)
Слайд 4 3.Историческая справка. (готовится учащимися, как дополнительное домашнее задание)
Впервые зависимость между корнями и коэффициентами квадратного уравнения установил знаменитый французский учёный Франсуа Виет (1540- 1603).
Франсуа Виет был по профессии адвокатом и много лет работал советником короля. И хотя математика была его увлечением, или как говорят сейчас хобби, благодаря упорному труду он добился в ней больших результатов. Виет в 1591 году ввёл буквенные обозначения для неизвестных и коэффициентов уравнений, что дало возможность записывать общими формулами корни и другие свойства уравнения.
Недостатком алгебры Виета было то, что он признавал только положительные числа. Чтобы избежать отрицательных решений, он заменял уравнения или искал искусственные приёмы решения, что отнимало много времени, усложняло решение и часто приводило к ошибкам. Много разных открытий сделал Виет. Но сам он больше всего дорожил установлением зависимости между корнями и коэффициентами квадратного уравнения, которая теперь называется его именем.
Первичное закрепление.
Цель: Учить применять теорему Виета
Слайд 5. Задания 1) 2) выполняются у доски с комментариями; 3) самостоятельно
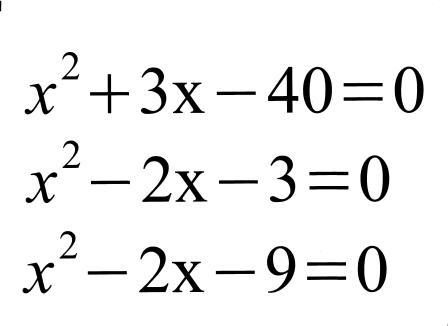
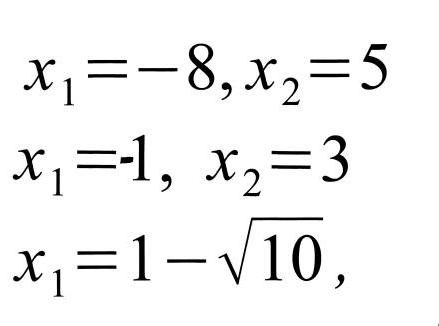
![]()
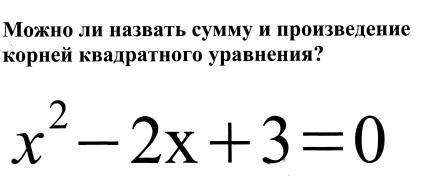 Слайд 6.
Слайд 6.
Возможно, что некоторые ученики ответят – да. На самом деле это уравнение не имеет корней, так как дискриминант отрицательный. Нужно дать им это проверить и сделать выводы.
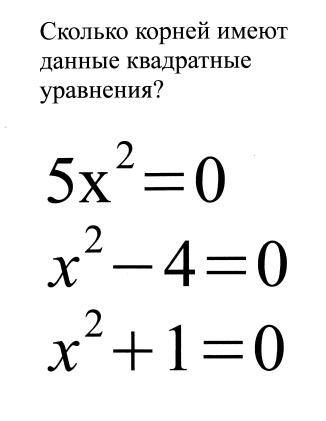 Слайд 7.
Слайд 7.
Устная работа
Может ли квадратное уравнение иметь 3 корня?
Почему?
Слайд 8.
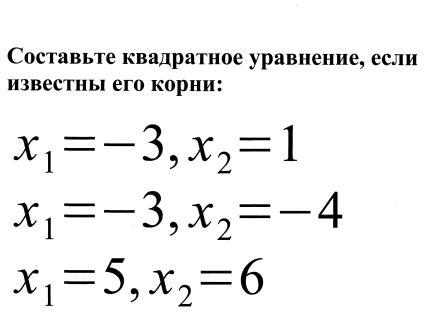
Ответы: 1) х2 +2х – 3 = 0
2) х2 +7х + 12 =0
3) х2 -11х + 30 =0
Изучаем следующую порцию материала.
Слайд 9. Сформулируйте утверждение, обратное теореме Виета.

Слайд 10.

Это утверждение позволяет подобрать целые корни для приведённого квадратного уравнения
Первичное закрепление по второму блоку изученного материала
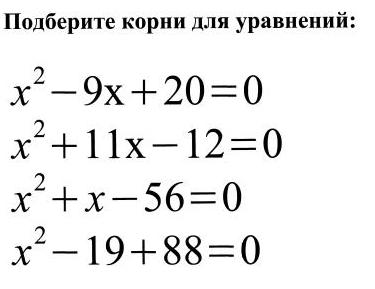 Слайд 11. Первое уравнение решаем у доски. Выясним , имеет ли оно корни? Как это сделать? Вычислим дискриминант. Д =1, что это значит?
Слайд 11. Первое уравнение решаем у доски. Выясним , имеет ли оно корни? Как это сделать? Вычислим дискриминант. Д =1, что это значит?
(уравнение имеет 2 корня).
Чему равна их сумма? (9) Чему равно их произведение? (20) Какие 2 целых числа удовлетворяют этим двум условия одновременно? (4 и 5).
Ответ: корнями уравнения являются числа 4 и 5.
 Решаем у доски методом подбора корней уравнения 2) и 3). Уравнение 4) решаем самостоятельно.
Решаем у доски методом подбора корней уравнения 2) и 3). Уравнение 4) решаем самостоятельно.
Слайд 12
Каков алгоритм решения квадратного
уравнения методом подбора корней?
Закрепление изученного материала.
Слайд 13 (у доски) Слайд 14 (у доски) Слайд 15 (самостоятельно)
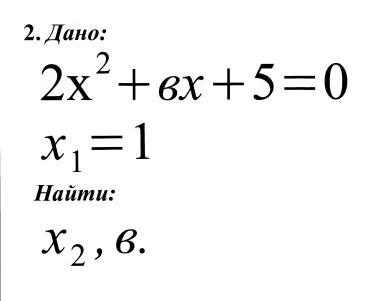
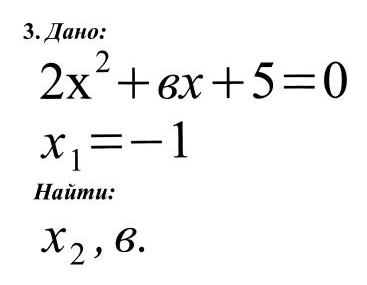
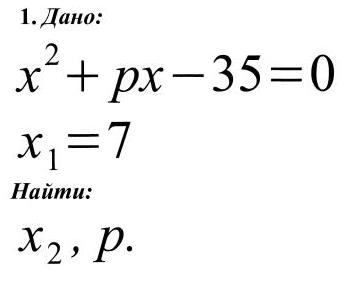
Ответы: 1) х2 =-5; р =-2. 2) х2 = 2,5; в = -7. 3) х2 =-2,5; в = 7.
Подводим итог урока
1. Сформулируйте прямую и обратную теоремы Виета.
2. Когда можно применять теоремы? (для проверки корней уравнения – прямая теорема; для подбора корней - обратная теорема)
3. Слайд 16

4.Каков алгоритм решения квадратного уравнения методом подбора корней?
5. Составьте приведённое квадратное уравнение, если известны его корни.
Слайд 17 Ответ: х2 -2=0
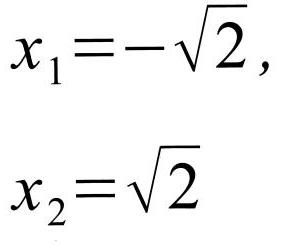
Рефлексия. Синквейн по теме урока
Домашнее задание. Выучить теоремы Виета. № 965, №968, №971. Н\З (необязательное задание, за выполнение которого выставляется оценка) 998.
Используемая литература.
А. Г. Мордкович. Алгебра 8 (в 2-х частях). Ч.1: Учебник.
А.Г. Мордкович, Т. Н. Мишустина, Е. .Е Тульчинская. Алгебра 8. Ч.2. Задачник.
Л.А. Александрова. Алгебра. Самостоятельные работы /Под ред. А.Г.Мордковича.
Е.Е. Тульчинская. Алгебра. Блицопрос. Пособие для учащихся.

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ