Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 31

г. Мурманска

Конспект и методическое сопровождение

урока геометрии в 9 классе

«Интересные свойства равнобедренной трапеции»

разработан

Сидоровой Анной Викторовной

учителем математики

первой квалификационной категории

г. Мурманск

2009 г.

Интересные свойства равнобедренной трапеции

Урок в 9 классе

Урок геометрии в 9 классе по теме «Интересные свойства равнобедренной трапеции» является уроком изучения нового материала. Этот урок можно провести при изучении темы: «Средняя линия трапеции» или при повторении всего курса планиметрии. Он будет очень полезным учащимся 11 классов при подготовке к ЕГЭ

Образовательные цели соответствуют требованиям к уровню подготовки выпускников, а так же месту урока в системе уроков по изучаемой теме и направлены на изучение новых свойств равнобедренной трапеции, усвоение и закрепление навыка решения задач с использованием этих свойств, а также отработке имеющихся навыков по этой теме, устранение пробелов в знаниях учащихся по данной теме.

Цели данного урока были спланированы как ожидаемые результаты, которые предполагается получить в процессе совместной деятельности с учащимися при их обучении, воспитании и развитии.

Развивающие цели данного урока направлены как на общее развитие ученика, так и на развитие у учащихся аналитико-синтезирующего, абстрактного мышления, развитие умений применять знания в различных ситуациях, развитие умений самостоятельной работы.

Воспитательные цели данного урока направлены на формирование положительной мотивации учения, созданию «ситуации успеха» на данном уроке. Исходя из типа урока, целей урока, содержания учебного материала отобраны методы и приёмы обучения.

1. Методы проблемного обучения:

эвристический метод (постановка проблемы и организация совместной поисковой деятельности по её разрешению.

2. Методы организации учебно-познавательной деятельности:

практические (закрепление практических умений и навыков происходит в ходе выполнения практических заданий), словесные. Выбранные методы оптимальны для данного урока и позволяют решить задачу личностно-ориентированного подхода в обучении на этом уроке.

Соответственно содержанию урока и особенностям класса выбраны формы обучения: общеклассная (на этапе изучения нового материала ведётся работа со всем классом, что необходимо для закрепления материала обязательного уровня всеми учениками класса), индивидуальная (учащиеся работают самостоятельно)

Цели и задачи урока:

• Повторить свойства равнобедренной трапеции; формулы площади трапеции; доказать новые свойства равнобедренной трапеции; рассмотреть задачи с их применением.

• Развивать умения анализировать, сопоставлять, логически мыслить, обобщать; развивать внимание, память, активность и самостоятельность.

• Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать в коллективе; воспитывать в учащихся личностную рефлексию: стал ли он сам для себя изменяющимся субъектом деятельности.

Оборудование: компьютер, мультимедийный проектор, печатные рабочие листы для работы учащихся на уроке.

Урок проводится с использованием мультимедийной презентации Power Point.

Ход урока:

Постановка целей урока.

Учитель: - Сегодня на уроке мы не только повторим известные вам свойства равнобедренной трапеции, но и рассмотрим новые интересные свойства равнобедренной трапеции, позволяющие более рационально решать задачи по этой теме. Может быть, в дальнейшем это поможет вам сэкономить время при сдаче ЕГЭ в 11 классе, когда будет дорога каждая минута.

Итак, трапеция. В “началах” Евклида этим термином назывались все четырехугольники кроме квадрата, ромба и прямоугольника, а также и усеченная пирамида. Слово  по-гречески означает “столик”. В современном смысле термин впервые встречается у древнегреческого математика Посидония.

Мы повторим известные нам свойства трапеции, изученные ранее.

Актуализация опорных знаний.

- Повторим основные свойства трапеции, заполнив пропуски в предложениях (на экране появляются слайды):

1) Трапецией называется четырёхугольник, у которого ______________________.

2) Трапеция называется равнобедренной (равнобокой), если __________________.

3) В равнобедренной трапеции углы __________________________________.

4) В равнобедренной трапеции диагонали ___________.

5) Средней линией трапеции называется отрезок, ______________________________.

6) Высотой трапеции называют отрезок прямой, ________________________.

7) Площадь трапеции равна произведению ____________________________________.

8) Трапеция называется описанной около окружности, если ______________________.

9) В трапецию можно вписать окружность, если ______________________________.

10) Центр вписанной окружности совпадает с точкой пересечения _______________.

11) Если трапеция равнобедренная, то точки касания с окружностью делят основания ___.

12) Отрезки касательных к окружности, проведённые из одной точки, _____________.

Задача 1

Найдите радиус окружности, если основания описанной около неё равнобедренной трапеции равны 4 см и 16 см.

Дано: окр.(О;r) вписана в трапецию ABCD, AD || BC, AD = 16 cм, ВС = 4 см

Найти: r

Решение:

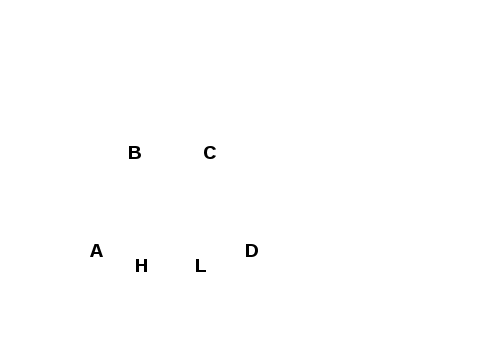
1. По свойству трапеции, описанной около окружности (вернуться к слайду

с данным свойством с помощью управляющей кнопки ),

АВ +CD = BC + AD, AB = CD (по условию), 2AB = BC + AD,

, АВ = 10 см.

2. Опустим высоты BH и CL.

3. Рассмотрим треугольник АВН: 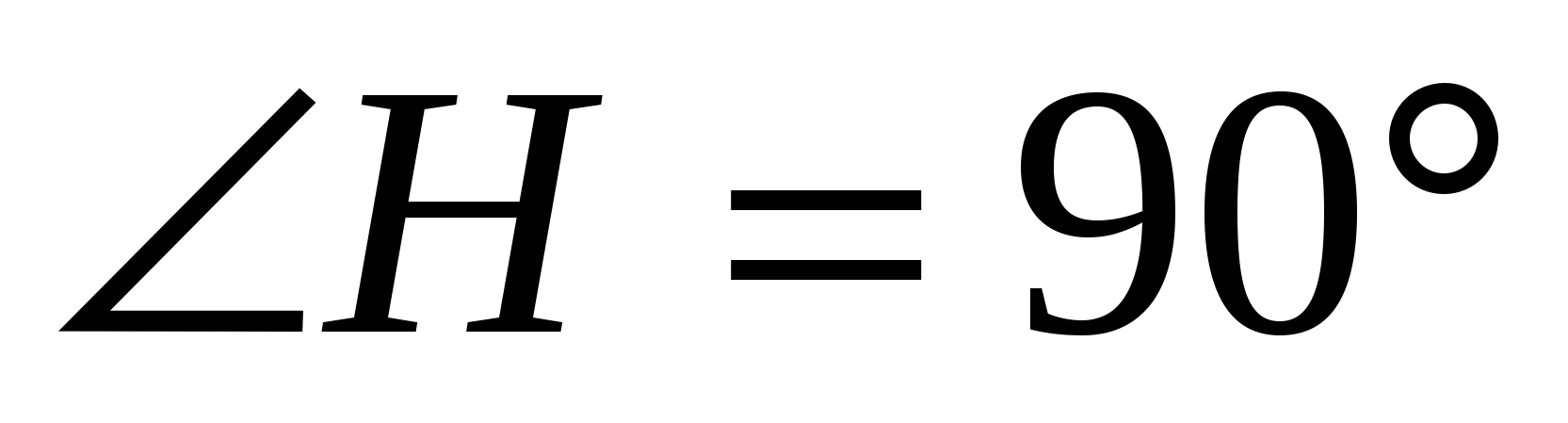, АН = ,

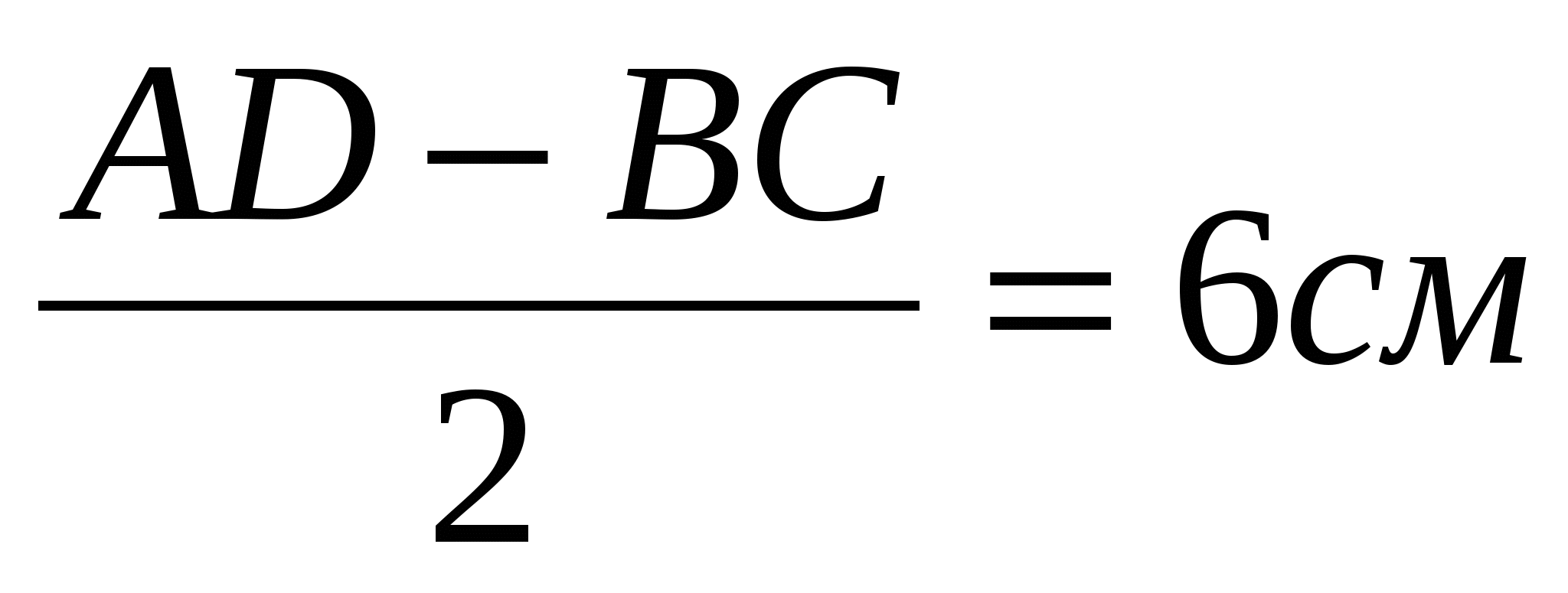AB = 10 см, по т. Пифагора:,

.

4. r =

Ответ: r = 4 cм.

Изучение нового материала.

Эту задачу можно решить другим способом, если бы вы знали

свойство1:

Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований: .

(Доказательство проводим устно, т.к. в печатной основе оно есть и в целях экономии времени).

Дано: окр.(О ; r) вписана в трапецию ABCD, AD || BС

A

B = CD, BC = a, AD = b, h – высота трапеции

Доказать:

Доказательство:

1) По свойству трапеции, описанной

около окружности: АВ + CD = AD + BC,

AB = CD, 2AB = AD + BC,

2)Опустим высоты ВН и СР.

3) Рассмотрим ΔАВН : ,АН =, ВН = h,

По т. Пифагора: ,

.

В ходе доказательства этого свойства мы доказали ещё одно

свойство2:

Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии трапеции.

Вернёмся к задаче 1 и решим её с применением этого свойства.

Другое решение задачи 1

, ,

Ответ: r = 4 см.

Какой способ вам больше понравился и почему? Этот способ короче, значит он более рациональный.

Закрепление полученных знаний.

Решим задачу 2 с применением новых двух свойств, доказанных на уроке.

Задача 2

Равнобедренная трапеция описана около круга. Боковая сторона трапеции делится точкой касания на отрезки длиной 18 и 32. Найдите площадь трапеции.

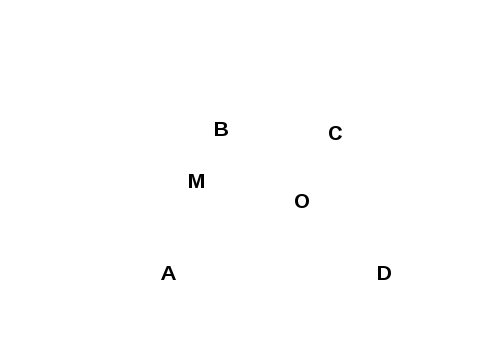
Дано: окр.(О ; r) вписана в трапецию ABCD, AD||BC, AB = CD

М АВ,AM = 32, MB = 18

Найти: S_ABCD

Решение: S = mh, где m – средняя линия, h – высота трапеции,

(анализ задачи сопровождается слайдами с помощью управляющих

кнопок)

1) т.к. боковая сторона равна средней линии, то

m = 18 + 32 = 50

2) По свойству отрезков касательных, проведённых

из одной точки, и свойству равнобедренной трапеции,

получаем: AD = 32 ∙ 2 = 64, BC = 18 ∙ 2 = 36.

3) Используя свойство: , получим

a = BC = 36, b = AD = 64

h² = 36 ∙ 64,

4) S = 50 ∙ 48 = 2400

Ответ: S = 2400

А теперь повторим, свойства равнобедренной трапеции, доказанные сегодня на уроке.

(На экране появляются рассмотренные за урок свойства)

Самостоятельная работа

Проверим, как вы усвоили эти свойства в ходе выполнения самостоятельной работы.

I вариант

В равнобедренную трапецию, основания которой 2 и 8, вписан круг. Найдите радиус этого круга.

II вариант

Около круга радиуса 2 описана равнобедренная трапеция с острым углом 30°. Найдите длину средней линии трапеции.

Закончим наш урок высказыванием великого учёного:

«Геометрия является самым могущественным средством

для изощрения наших умственных способностей и дает нам

возможность правильно мыслить и рассуждать»

(_________________________)

Для того чтобы узнать фамилию этого учёного, мы зачеркнем из таблицы полученные в ходе самостоятельной работы ответы:

2

12

5

9

2400

2,5

20

4

40

8

16

М

Г

А

Л

О

И

Л

П

Е

Д

Й

Ответ: Галилей.

Подведение итогов. Постановка домашнего задания.

И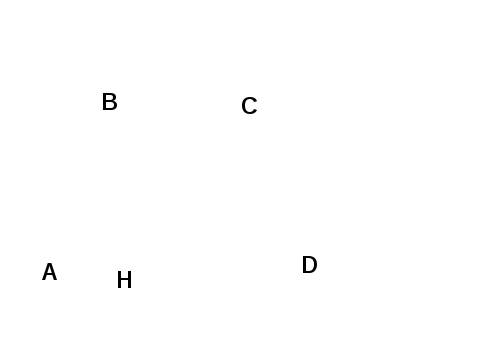

тоги урока подводятся с опорой на конспект урока. Затем оценивается работа учащихся, выставляются оценки за урок. Предлагается домашнее задание.

Мне бы хотелось познакомить вас ещё с некоторыми свойствами равнобедренной трапеции, которые я предлагаю вам доказать самостоятельно:

Свойство 3:

• В равнобедренной трапеции проекция диагонали на большее

основание равна средней линии трапеции.

Свойство 4:

• Е

  

  сли в равнобедренной трапеции диагонали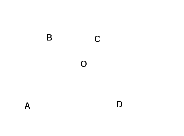

взаимно перпендикулярны, то её высота равна средней линии.

Свойство 5:

• Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты, т.е..

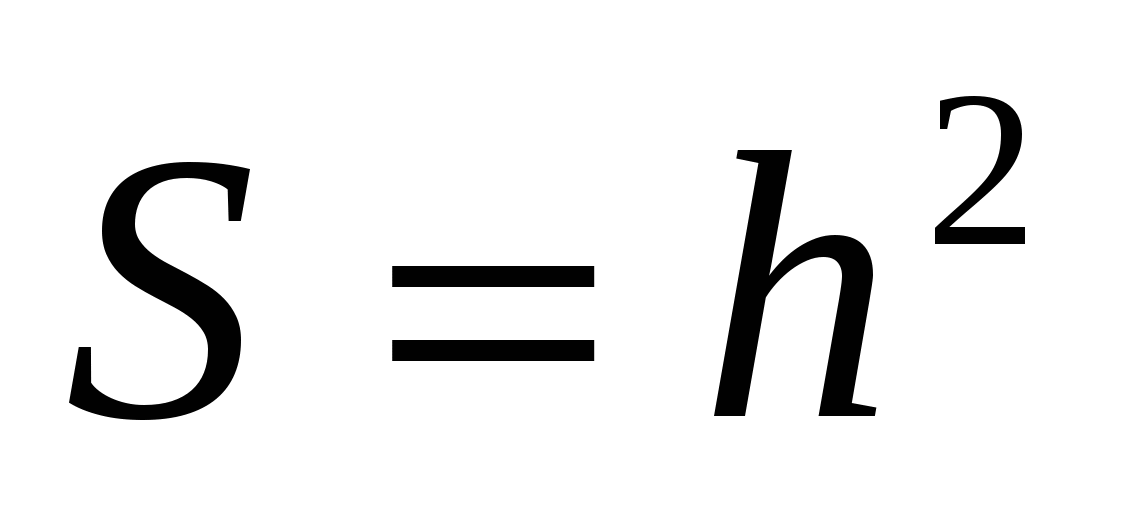Я предлагаю вам решить дома задачи с применением этих свойств:

• Найдите площадь равнобедренной трапеции, если её диагональ, равная 10, образует с основанием угол, косинус которого равен 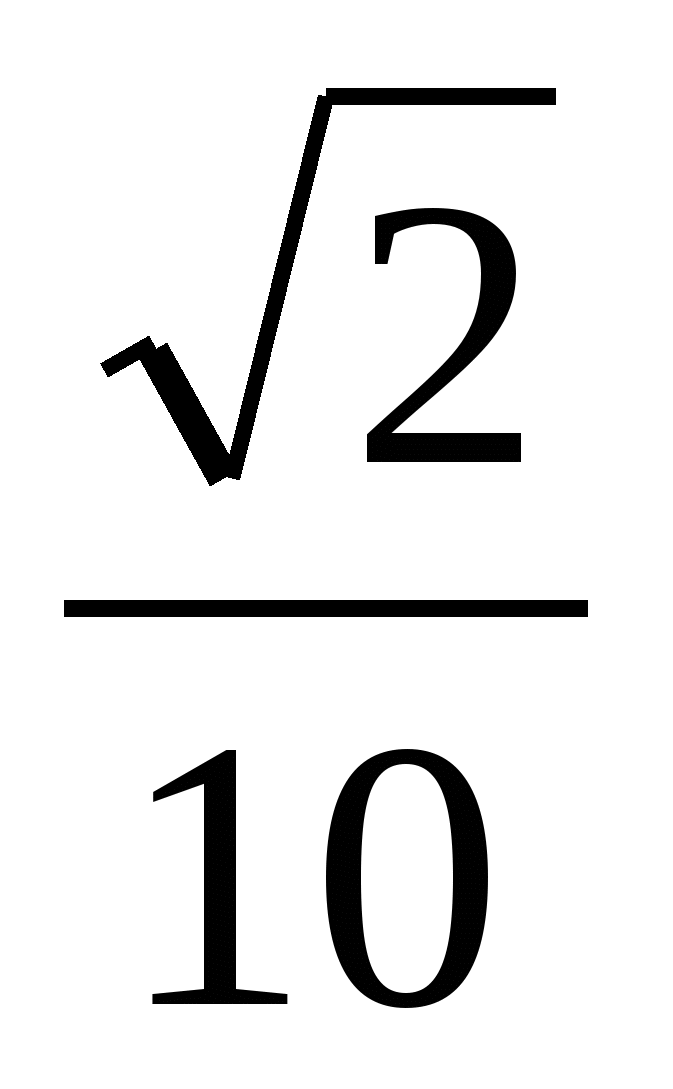. (ЕГЭ- 2007, В11)

• В равнобедренной трапеции диагонали взаимно перпендикулярны. Найдите площадь трапеции, основания которой равны 10 и 26.

Большое спасибо за урок!

(Показывается заключительный слайд)

Используемая литература:

1. Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.Геометрия: Учеб. для 7-9 кл. сред.шк./-3-е изд.-М.: Просвещение, 2008.

2. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Курс геометрии 8-го класса в задачах (для классов с углублённым изучением математики, специализированных классов естественно-технического профиля).Львов .Журнал «Квантор» 1991

3. Ковалева Г.И., Бузулина Т.И., Безрукова О.Л., Розка Ю.А. Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и другим формам выпускного и вступительного экзаменов. Волгоград: Учитель, 2007

4. Симонов А.Я., Бакаев Д.С., Эпельман А.Г. и др.Система тренировочных задач и упражнений по математике. М.: Просвещение, 1991.