МОУ «Октябрьская средняя общеобразовательная школа» Ардатовского района РМ

ПЕДАГОГИЧЕСКАЯ МАСТЕРСКАЯ

Гражданин мира

Пифагор и его теорема

Урок разработала и провела

учитель математики Михатова М. Н.

ОКТЯБРЬСКИЙ

ТЕМА УРОКА: Гражданин мира

Пифагор и его теорема

ЦЕЛИ:

• Реализация принципа умственного развития учащихся.

• Развитие познавательной и творческой деятельности учащихся.

ЗАДАЧИ УРОКА:

• Прививать навыки самостоятельного поиска новых закономерностей, пробуждать их любознательность.

• Развитие культуры коллективного умственного труда.

• Формирование и развитие интереса учащихся к занятиям математикой, расширить математический кругозор учащихся.

ТИП УРОКА: Педагогическая мастерская

ОБОРУДОВАНИЕ:

• Портрет Пифагора

• Различные таблицы

• Карточки-задания

Ход мастерской:

1. Индуктор

Мастер:

Сегодня мы в нашей мастерской совершим пусть маленькие, но открытия. Давайте со всеми делиться теми идеями, которые придут нам в голову по ходу дела. Помните, любая мысль может дать нам новое направление поиска.

Сначала давайте представим себе, что мы находимся в сказочном саду, где можем встретить любого ученого, поэта, музыканта. Да, вот я вижу Пифагора, замечательного математика VI века до н.э. Он много путешествовал по странам Востока, а потом основал на юге Италии философско-математическую школу.

(Пифагор медленно и задумчиво входит)

Мастер:

Приветствую Тебя о таинственный Пифагор! Как жаль, что мы мало знаем о тебе! Не хочешь ли Ты сам рассказать об основах своего учения?

Пифагор:

Явления всей Вселенной подчинены определенным числовым соотношениям. Число - это закон и связь мира, сила, царящая над богами и смертными. Все упорядочивается в соответствии с числами - вот основа моего учения. Вы слышите звуки музыки? (Звучит музыка). Мне удалось установить связь между длиной струны музыкального инструмента и издаваемым им звуком. И тогда я решил, что не только законы музыки, но и вообще все на свете можно выразить с помощью чисел. Я утверждаю: «Числа правят миром!»

2. Социоконструкция

Мастер:

А вы, ребята, согласны с Пифагором, что числа управляют мировым порядком? Обсудите с соседом по парте и запишите каждый свой ответ на листе №1.

3. Социализация

Ответы зачитываются вслух и откладываются на край стола.

4. Разрыв

Много открытий сделал Пифагор, но главное - его знаменитая теорема. В настоящее время имеется около 500 различных доказательств теоремы Пифагора. Доказательство этой теоремы триумф древнегреческой мысли. Предлагаю каждому из вас самостоятельно провести одно из доказательств под моим руководством. Но вначале ответьте на следующие вопросы и обсудите их в паре.

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам.

ОТВЕТЫ:

1.Треугольник называется прямоугольным, если один из углов равен 90º.

2.Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катеты.

3.Площадь квадрата равна квадрату его стороны

4.Площадь прямоугольного треугольника равна половине произведения его катетов

5.Социализация

Мастер:

А сейчас переверните карточки и сравните свои ответы с правильными. Поднимите руки все, кто правильно ответил на все вопросы. Молодцы!

6.Социоконструкция.

Мастер:

Приступим к следующему этапу нашего урока. Откройте тетради, запишите число и кратко тему урока «Пифагор и его теорема». Теорема Пифагора звучит так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»

• Начертите в тетрадях прямоугольный треугольник. Обозначьте катеты этого треугольника а, в , а гипотенузу с.

• Постройте квадрат, сторона которого равна а + в.

• На сторонах квадрата отметьте по одной точке, делящей эти стороны на отрезки а и в так, чтобы к каждой вершине квадрата примыкали отрезки а и в.

• Соедините отрезками точки, расположенные на соседних сторонах квадрата. Посмотрите, на какие фигуры при этом разобьется исходный квадрат. Покажите, что полученные треугольники равны исходному прямоугольному треугольнику. Укажите признак равенства треугольников (второй признак).

• Чему равны стороны полученного внутреннего четырехугольника? Чему равны углы этого четырехугольника? Какой из этого вывод о внутреннем четырехугольнике можно сделать? (с, 90º, квадрат)

• Рассмотрим теперь вопрос о том, как связать между собой площади полученных треугольников и квадратов. Обозначьте: S - площадь исходного квадрата, S∆ - площадь исходного треугольника, S◊ - площадь внутреннего квадрата.

• Зная стороны прямоугольного треугольника и квадратов, напишите формулы для их площадей.

• Подставьте полученные формулы в равенство для площадей. Какое равенство при этом получается? Раскрывая квадрат и приводя подобные члены, окончательно получаем равенство

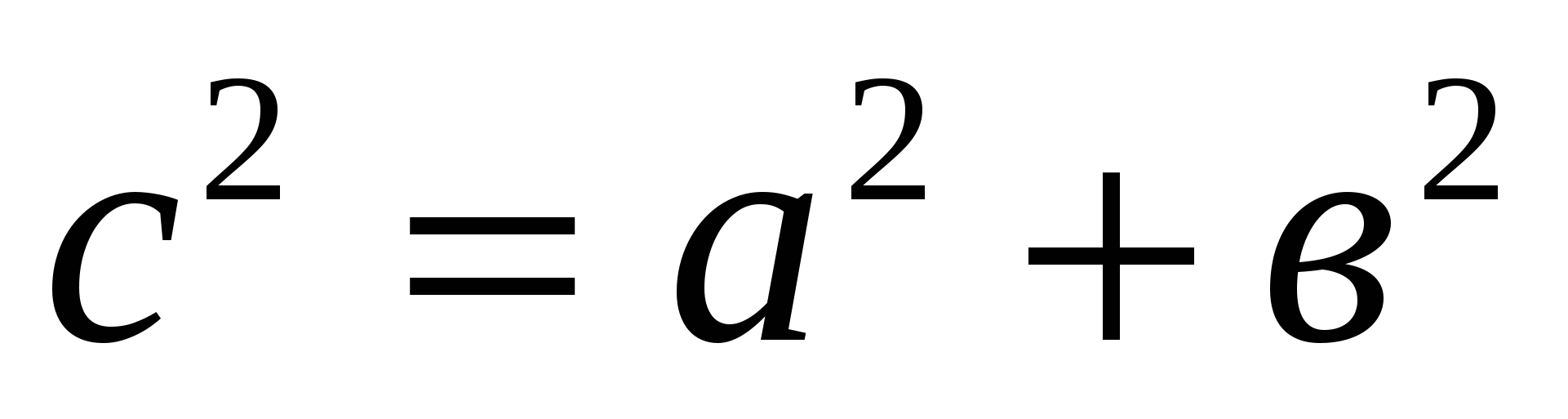
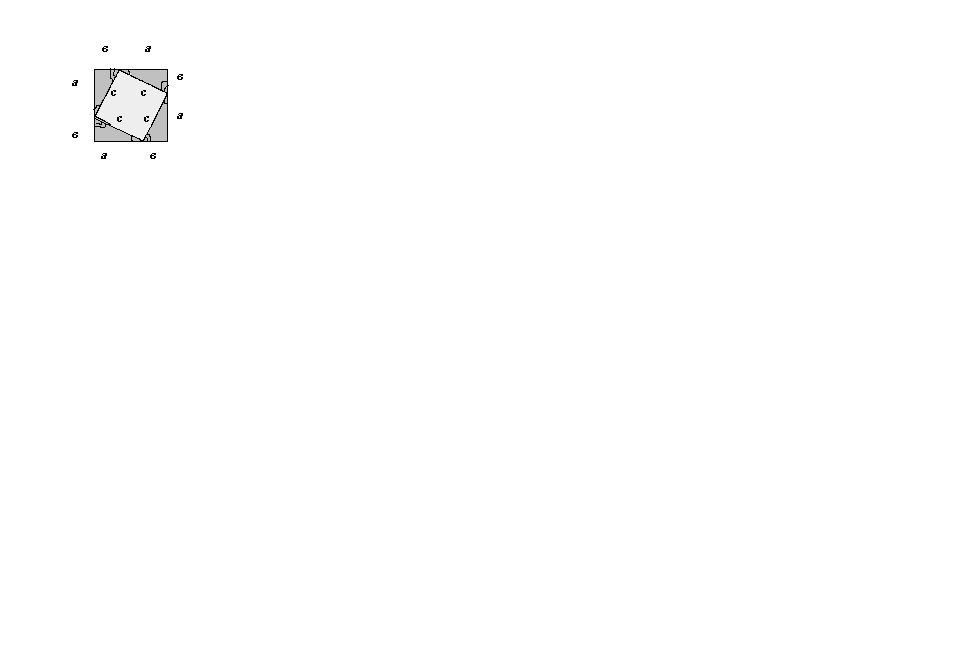
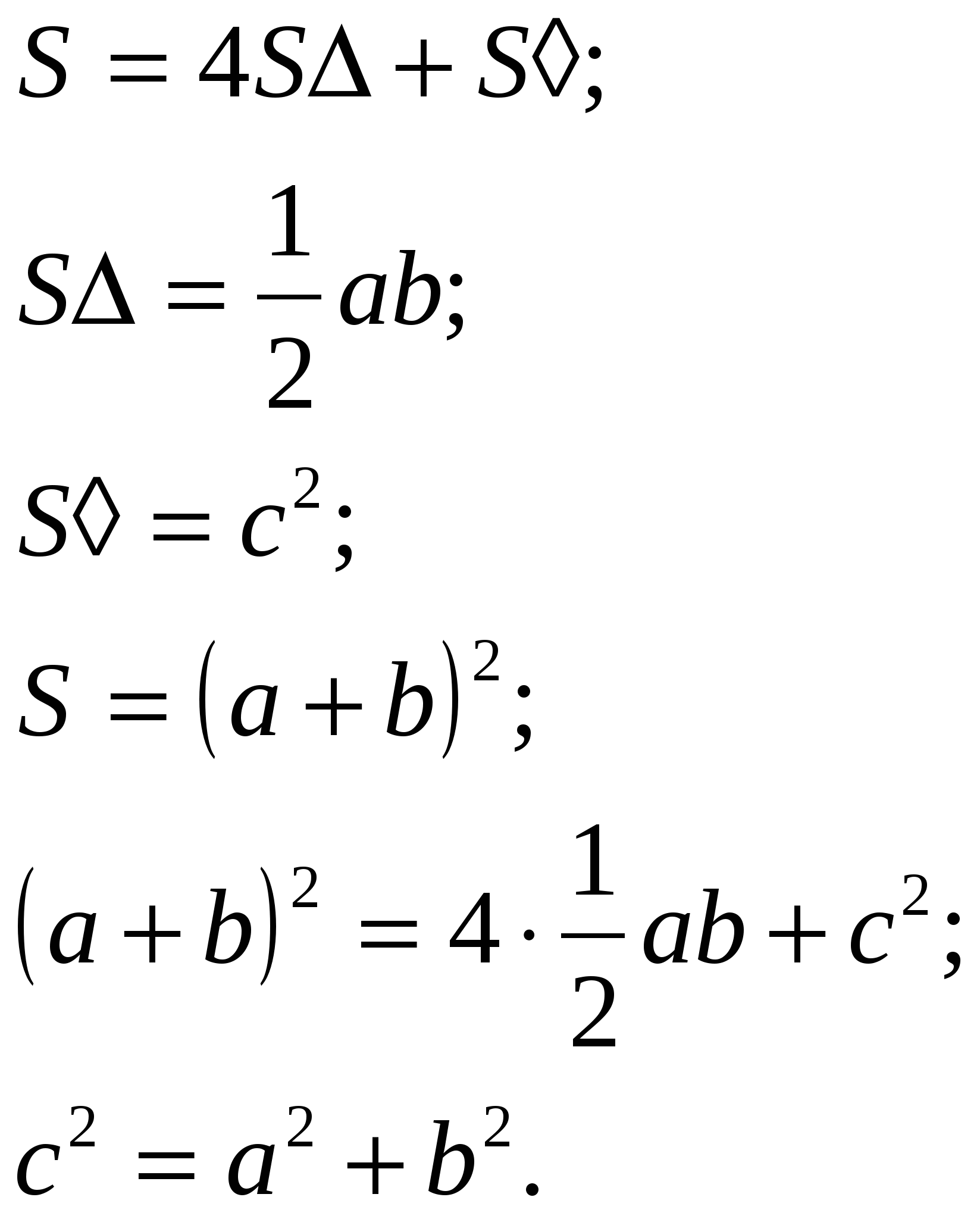
Посмотрите, какое красивое доказательство имеет эта теорема! Давайте все вместе повторим: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».

7.Деконструкция

Для усвоения теоремы Пифагора в классе решим задачи из учебника

№ 483(а, б, г); 484(а, в, д); 485.

(Решение задач в парах).

8.Афиширование

Обсуждение решения задач (один из пары) у доски.

9.Рефлексия (итог)

Вот и подошла к концу наша мастерская на тему: «Гражданин мира. Пифагор и его теорема». Действительно Пифагора можно назвать гражданином мира! Он первым начал рассуждать о числах. Много легенд рассказывали греки об этом мыслители. Его ученики уверяли даже, что он был сыном самого солнечного бога Апполона, что его бедро было сделано из чистого золота, а когда он подошел к одной реке, то она вышла из берегов, чтобы приветствовать Пифагора! Если отбросить все сказки и выдумки, то окажется, что Пифагор очень много сделал для развития науки (хотя он начинал

не как ученый, а как победитель Олимпийских игр по кулачному бою!). Его знаменитая теорема была первым утверждением, связывавшим длины сторон треугольников. Возникла целая наука тригонометрия («тригон» - по-гречески означает «треугольник»).

Сейчас тригонометрию применяю даже для измерения расстояний между космическими кораблями.

Запишите задание на дом:

ПРИЛОЖЕНИЯ

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам.

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам.

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам.

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам.

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам.

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам.

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам.

Лист №2

ВОПРОСЫ:

1. Какой треугольник называется

прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Формула площади квадрата.

4. Формула площади прямоугольного треугольника

по его катетам

ОТВЕТЫ:

1.Треугольник называется прямоугольным,

если один из углов равен 90º.

2.Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катеты.

3.Площадь квадрата равна квадрату его стороны

4.Площадь прямоугольного треугольника равна половине произведения его катетов

ОТВЕТЫ:

1.Треугольник называется прямоугольным,

если один из углов равен 90º.

2.Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катеты.

3.Площадь квадрата равна квадрату его стороны

4.Площадь прямоугольного треугольника равна половине произведения его катетов

ОТВЕТЫ:

1.Треугольник называется прямоугольным,

если один из углов равен 90º.

2.Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катеты.

3.Площадь квадрата равна квадрату его стороны

4.Площадь прямоугольного треугольника равна половине произведения его катетов

ОТВЕТЫ:

1.Треугольник называется прямоугольным,

если один из углов равен 90º.

2.Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катеты.

3.Площадь квадрата равна квадрату его стороны

4.Площадь прямоугольного треугольника равна половине произведения его катетов

ОТВЕТЫ:

1.Треугольник называется прямоугольным,

если один из углов равен 90º.

2.Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катеты.

3.Площадь квадрата равна квадрату его стороны

4.Площадь прямоугольного треугольника равна половине произведения его катетов

ОТВЕТЫ:

1.Треугольник называется прямоугольным,

если один из углов равен 90º.

2.Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катеты.

3.Площадь квадрата равна квадрату его стороны

4.Площадь прямоугольного треугольника равна половине произведения его катетов

s₁

S

s₂

S = s_{1 +} s₂

Для любого прямоугольного треугольника площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

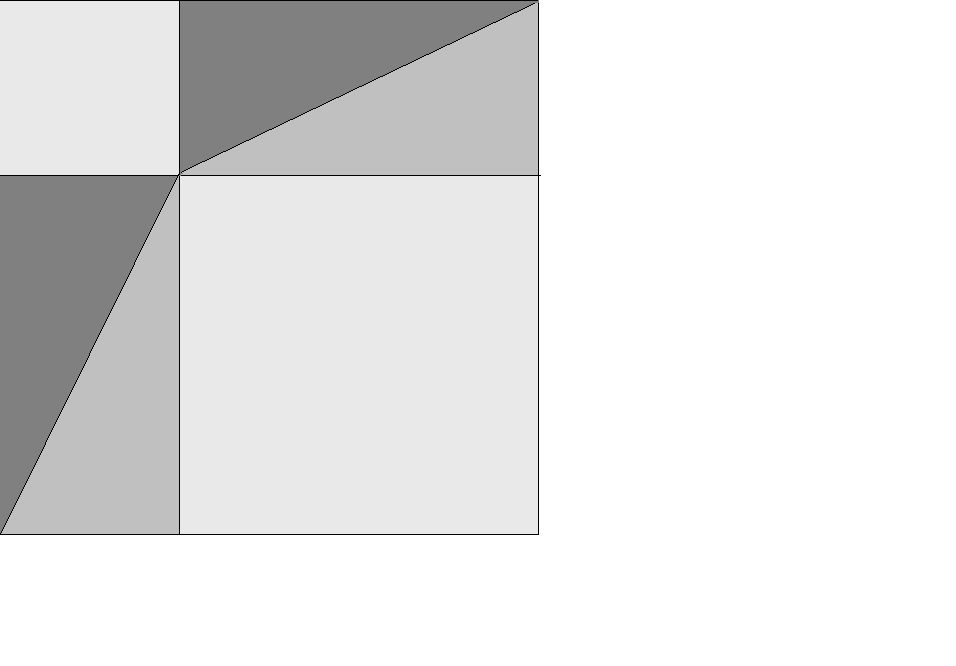
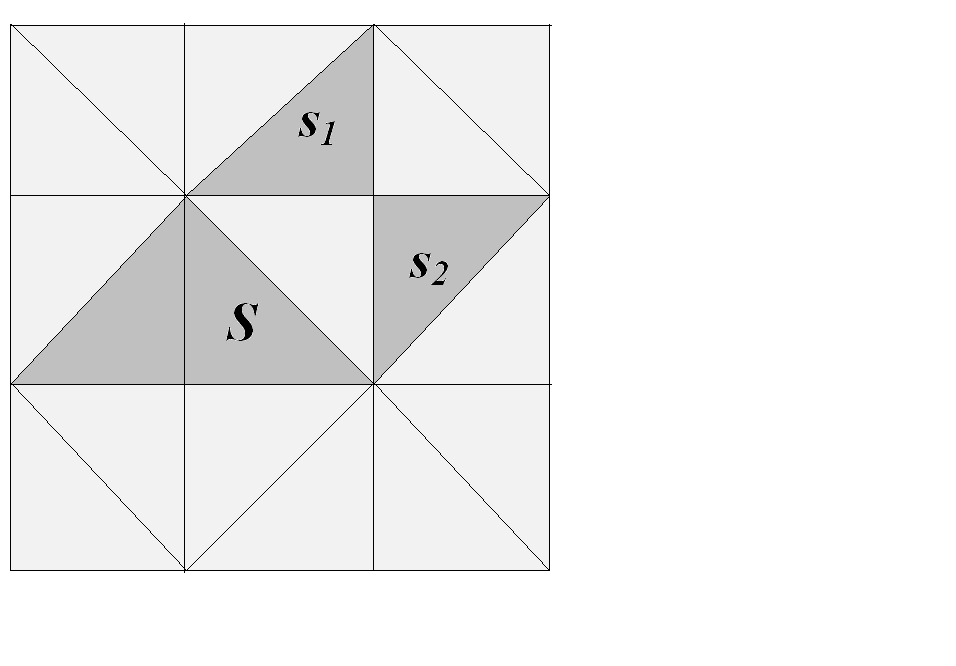
S = s_{1 +} s₂

Для любого прямоугольного треугольника площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

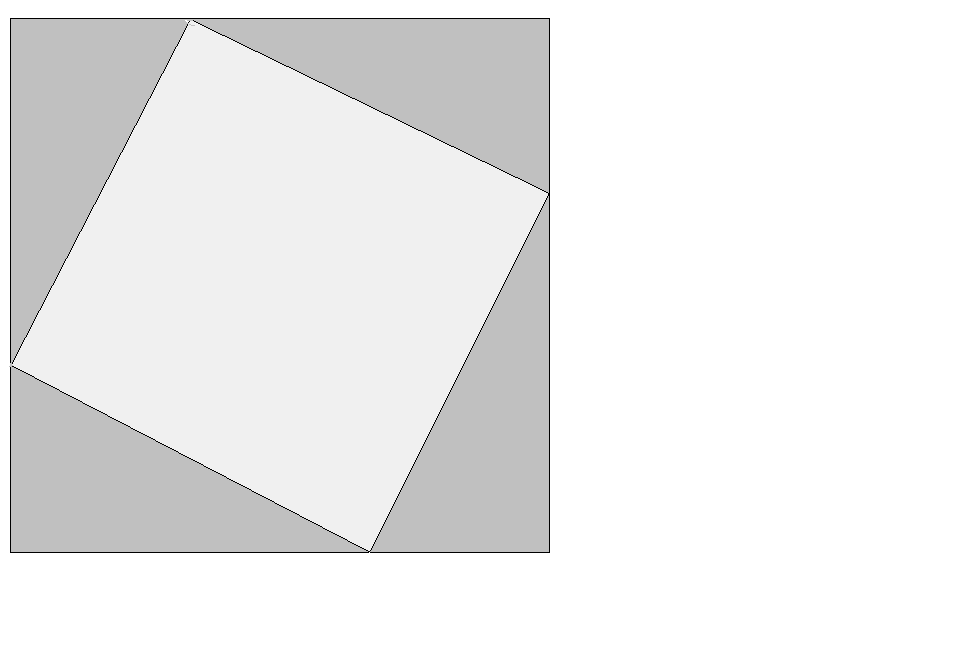
Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

МОУ «Октябрьская средняя общеобразовательная школа» Ардатовского района РМ

АНАЛИЗ УРОКА ГЕОМЕТРИИ

Гражданин мира

Пифагор и его теорема

Урок разработала и провела

учитель математики Михатова М. Н.

ОКТЯБРЬСКИЙ

Анализ урока геометрии в 8 классе

ТЕМА УРОКА: Гражданин мира

Пифагор и его теорема

Специфика урока по теме «Гражданин мира Пифагор и его теорема» состоит в обращении к образному мышлению учащихся, он проводится в форме педагогической мастерской. На этом уроке создаются психологические условия для саморазвития, самовыражения в ходе овладения знаниями, проводится работа с каждым учеником в рамках одновременной работы со всем классом. Содержание урока подбиралось таким образом, чтобы рассмотреть подробно доказательство теоремы Пифагора и вовлечь каждого учащегося в активную и посильную деятельность.

На уроке решались следующие задачи:

• Привить учащимся навыки самостоятельного поиска новых закономерностей, пробуждать их любознательность.

• Развитие культуры коллективного умственного труда.

• Формирование и развитие интереса учащихся к занятиям математикой, расширить математический кругозор учащихся.

Использовались следующие формы организации познавательной деятельности: фронтальная, парная, индивидуальная. Они выбирались так, чтобы на каждом этапе урока вовлечь каждого ребёнка в учебную деятельность, вселить уверенность в собственные силы. Задания в ходе изучения нового материала, на применение полученных знаний даются в парах для обеспечения занятости и развития каждого ученика.

Структура урока полностью соответствует технологии педагогической мастерской.

Время рационально было распределено между 9 этапами

урока:

1. Индуктор

2. Социоконструкция

3. Социализация

4. Разрыв

5.Социализация

6.Социоконструкция.

7.Деконструкция

8.Афиширование

9.Рефлексия (итог)

Главный акцент на уроке делался на самом доказательстве теоремы Пифагора - этап 5 социоконструкция. Для раскрытия нового материала использовалось сочетание побуждающего и поискового методов обучения. Такое содержание позволяет придать уроку личностно-смысловую направленность.

Контроль усвоения знаний, умений и навыков был организован в форме обсуждения решения задач (один из пары) у доски и проходил на этапе 8 - афиширование.

На уроке использовались следующие средства обучения

• Таблицы

• Карточки-задания

• Портрет Пифагора

Высокая работоспособность школьников в течение всего урока обеспечивалась за счет способности к самостоятельному планированию учебных действий.

На уроке поддерживалась хорошая психологическая атмосфера, общение, было реализовано воспитательное влияние личности учителя за счет использования исторического материала, который развивает интерес учащихся к занятиям математикой, расширяет математический кругозор. Это этапы 1- Индуктор, 4 - Разрыв, 9 - Рефлексия.

На данном уроке удалось практически полностью реализовать все поставленные задачи.

S - площадь исходного квадрата

S_∆ - площадь исходного

треугольника

S_◊-площадь внутреннего

квадрата