Задачи с практическим содержанием по теме "Четырёхугольники"
Питимирова Надежда Алексеевна
учитель математики
первая категория
МКОУ «Чебаклинская СОШ» Большеуковского района
Омской области
Задачи с практическим содержанием
по теме «Четырёхугольники»
Представленный ресурс можно использовать на уроке – практикуме
по теме Четырёхугольники»
Задача №1
Как найти расстояние между двумя недоступными для геодезиста точками А и В, используя признак параллелограмма.
Решение: 1случай
Расстояние до точек А и В измерить геодезист не может.
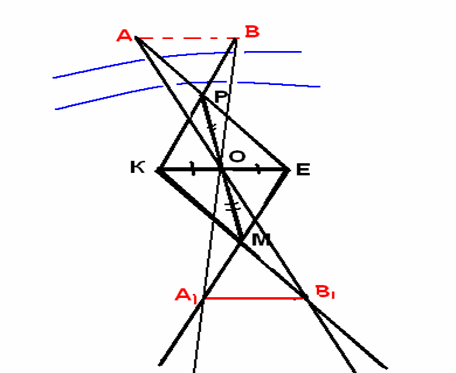
Отметим в доступном месте точки К, О и Е так, что КО=ОЕ.
Соединим АЕ и КВ (не измеряя) так, чтобы они пересеклись в доступной точке Р . Строим отрезок РО и равный ему ОМ . Получили параллелограмм КМЕР ( по признаку). Точку В1 получаем пересечением прямых КМ и АО, а точку А1 – пересечением МЕ и ВО.
Отрезок А1В1= АВ.
Докажем, что это верно. Точка О – центр параллелограмма, следовательно является центром симметрии. Действительно, при преобразовании симметрии относительно центра О точка К переходит в точку Е , точка Р — в точку М, прямая РЕ — в прямую КМ,
КР в МЕ, прямая РМ— в себя, а точка В - точка пересечения прямых КР и BО — в точку А1 пересечения ЕМ и BО. Аналогично точка А при этом преобразовании переходит в точку В1, поэтому отрезок АВ симметричен отрезку А1В 1 относительно точки О.
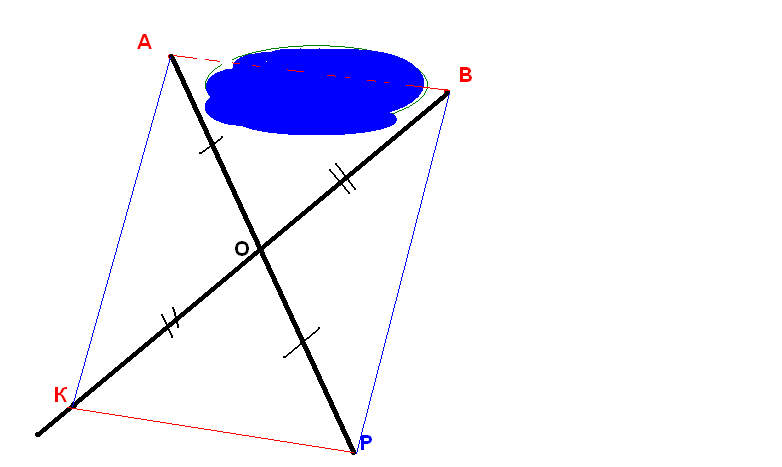
2 случай
С помощью приборов можно измерить расстояние ОА и ОВ. Достроить до параллелограмма АВРК, пользуясь признаком параллелограмма.
По свойствам параллелограмма КР=АВ. Измерить отрезок КР .
Задача №2
Школьная мастерская изготовила партию пластин четырёхугольной формы. Как проверить, будет ли иметь пластина форму прямоугольника, располагая лишь линейкой с делениями.
Решение:
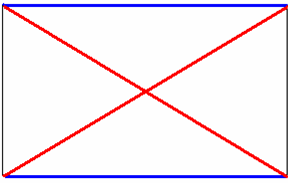
1) Измерим пары противоположных сторон четырёхугольника.
Если они равны,то пластина имеет форму параллелограмма
(по признаку параллелограмма: Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник является параллелограммом).
2) Измерим диагонали данной пластины, если они равны, то параллелограмм является прямоугольником
(по признаку прямоугольника: Если диагонали параллелограмма равны, то он является прямоугольником)
Необходимо сделать 6 измерений
Задача №3

Фруктовый сад имеет форму прямоугольника, стороны которого относятся как 16:11, причём его ширина на 250 м меньше длины.
За сколько времени сторож может обойти вдоль забора весь участок, идя со скоростью 4км/ч?
Решение:
На ширину участка приходится 11 частей, а на длину – 16 частей.
16-11=5 частей приходится на 250 м
250:5 =50м приходится на одну часть
(16+11)*2= 54 части приходится на длину всего забора
54*50=2700м= 2,7км–длина забора
2,7:4=0,675ч=40,5 мин сторож может обойти вдоль забора весь участок, идя со скоростью 4км/ч
Ответ: за 40,5минут
Задача № 4
Разделите пополам угол, вершина которого недоступна
Решение:1способ
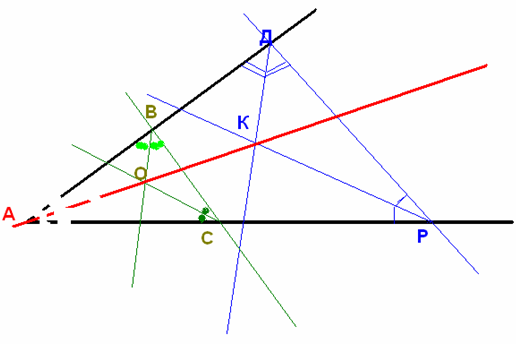
Проведём прямую ДР, получили ∆АДР, построим биссектрисы углов Д и Р. Точка К- точка пересечения биссектрис, а в треугольнике биссектрисы пересекаются в одной точке, следовательно искомая биссектриса должна проходить через эту точку.
Аналогично получаем точку О в ∆АВС.
Точки О и К – точки биссектрисы угла А.
Соединяем точки О и К.
Т.О. Прямая ОК делит угол пополам
2 способ
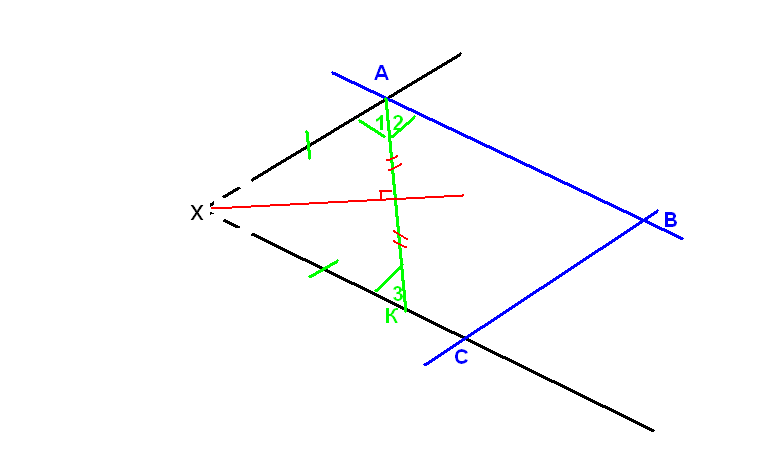
Проведём прямые АВ и ВС параллельно сторонам угла. Получили параллелограмм ХАВС с недоступной точкой Х.
Биссектриса АК отсекает от параллелограмма равнобедренный ∆ХАК,
По свойству равнобедренного треугольника биссектриса совпадает с медианой и высотой. Таким образом, можно построить серединный перпендикуляр к отрезку АК, который разделит данный угол Х пополам.
Задача №5
Столяру нужно изготовить подставку в форме четырёхугольника.
Сколько и какие размеры он должен измерить для выполнения заказа?
Решение этой проблемы дл столяра зависит от того, какие у него имеются инструменты


Рулетка
Циркуль Угломер
А) Форма параллелограмма
1)
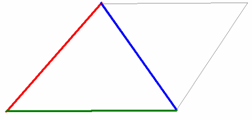 Три измерения:
Три измерения:
смежные стороны и диагональ
( циркуль и рулетка)
2)
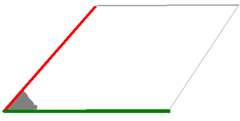
Три измерения:
смежные стороны и угол между ними
( угломер и рулетка)
Б) Форма прямоугольника
 Два измерения:
Два измерения:
смежные стороны
( при измерении используем только рулетку, при построении – угломер или другой инструмент для построения прямого угла)
В) Форма ромба
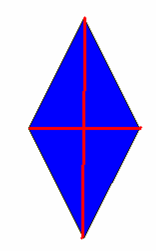
Два измерения:
диагонали ромба
( при измерении используем только рулетку, при построении – угломер или другой инструмент для построения прямого угла)
Г) Форма квадрата Д) равносторонний треугольник

Одно измерение: сторона
Задача №6
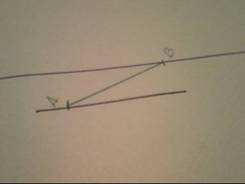
У плотника имеется только один инструмент – двусторонняя линейка без делений. Ему необходимо разделить кусок доски пополам. Как это сделать? (длина доски больше ширины линейки)
Решение:
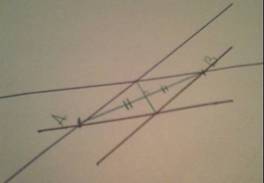
Решение задачи основано на свойстве ромба: диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам



Задача №7
В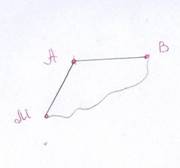 старинном замке пол был покрыт паркетом. Каждая плитка имела форму равнобедренной трапеции, от которой остались лишь обломки. Среди них имеется обломок, у которого сохранилось меньшее основание и половина боковой стороны трапеции. Задача реставратора восстановить форму плитки (с помощью циркуля и линейки)
старинном замке пол был покрыт паркетом. Каждая плитка имела форму равнобедренной трапеции, от которой остались лишь обломки. Среди них имеется обломок, у которого сохранилось меньшее основание и половина боковой стороны трапеции. Задача реставратора восстановить форму плитки (с помощью циркуля и линейки)
Р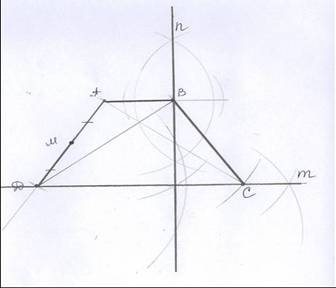 ешение:
ешение:
Восстанавливаем боковую сторону АД. Строим прямую п перпендикулярную АВ, затем через точку Д прямую m перпендикулярную п. Прямые АВ и m параллельны. Далее воспользуемся свойством диагоналей равнобедренной трапеции ( диагонали равны), построим окружность с центром в точке В радиусом ВД. Восстановили четвёртую вершину трапеции.
АВСД- искомая трапеция.
Задача №8
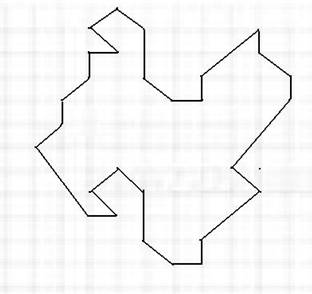
На фотографии изображён образец паркета «Белочка».
Определить, какая фигура является основой для составления данного паркета, и вычислить площадь одной «белочки».

Решение: 1способ
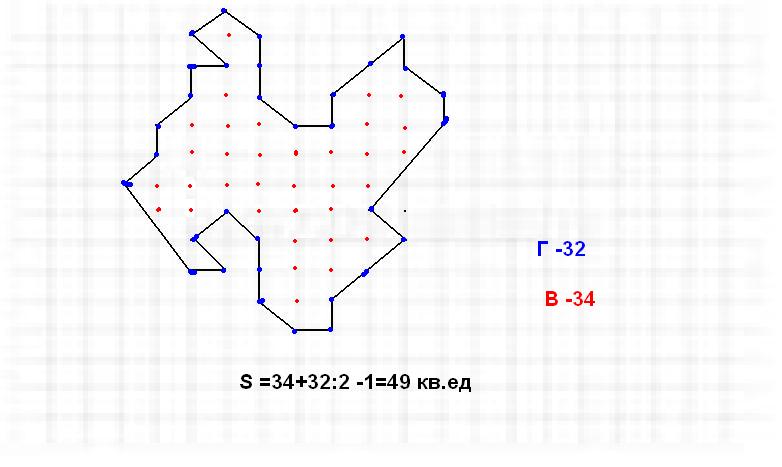
По формуле Пика
Площадь многоугольника с целочисленными вершинами равна
S= В + Г/2 − 1,
Где В есть количество целочисленных точек внутри многоугольника,
а Г — количество целочисленных точек на границе многоугольника.
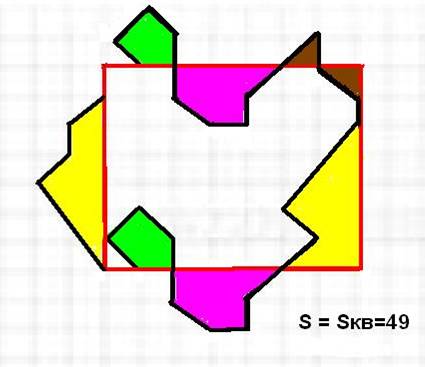
2 способ.
Площади равносоставленных фигур равны.
Выяснить перекраиванием, что данная фигура и квадрат равносоставлены, следовательно, их площади равны.
Определив сторону квадрата, находим площадь фигуры.
Литература:
1) Сборник задач по математике с решениями. 8—11 кл. / В. К. Егерев, В. В. Зайцев, Б. А. Кордемский и др.; Под ред. М. И. Сканави.
2) Задачи к урокам геометрии, 7-11 классы. (Зив Б.Г.) 1998
3) Геометрия, 7—9 классы (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.) 2010
Иллюстрации:
1. из личного архива
2. http://images.yandex.ru/yandsearch?

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ