Сахапова Гульнара Магдановна

МБОУ «СОШ №21» г.Альметьевска РТ

Учитель информатики

Тема урока: Таблицы истинности

Цель урока: познакомить учащихся с принципами построения таблиц истинности для логических функций.

Задачи урока:

• обучающие – усвоение учащимися понятий «логическая функция», «таблица истинности» и «равносильные логические функции», ознакомление с порядком выполнения логических операций и алгоритмом построения таблиц истинности; выработка навыка построения таблиц истинности для логических функций;

• развивающие – развитие логического и алгоритмического мышления учащихся; развитие памяти и внимания;

• воспитательные – воспитание культуры общения; воспитание чувства ответственности за свой труд.

Тип урока: урок формирования знаний умений с элементами практики.

Возраст учащихся: 11 класс

Оборудование:

• программа MS Excel;

• презентация по теме урока;

• раздаточный материал для практической работы.

План урока:

1. Организационный момент – 1 минута;

2. Актуализация опорных знаний – 5 минут

3. Объяснение нового материала – 10 минут

4. Закрепление изученного материала – 8 минут

5. Выполнение практической работы – 16 минут

6. Постановка домашнего задания – 2 минуты

7. Подведение итогов урока – 3 минуты

Ход урока

1. Организационный момент

На прошлом уроке мы познакомились с понятием «логическое выражение», узнали, что логические выражения могут принимать значения «истина» или «ложь», а также познакомились с такими логическими операциями, как инверсия, конъюнкция, дизъюнкция, импликация и эквиваленция.

2. Актуализация опорных знаний

1

и

м

п

л

и

к

а

ц

и

я

2

п

о

н

я

т

и

е

3

а

л

г

е

б

р

а

4

с

у

ж

д

е

н

и

е

5

д

и

з

ъ

ю

н

к

ц

и

я

6

и

с

т

и

н

а

По горизонтали:

1. Высказывание, которое ложно тогда и только тогда, когда А истинно и В ложно

2. Форма мышления, которая выделяет существенные признаки предмета или класса предметов, отличающие его от других

3. Наука об общих операциях, которые могут выполняться над различными математическими объектами

4. Форма мышления, в которой утверждается или отрицается связь между предметом и его признаком, отношения между предметами или факт существования предмета

5. Объединение двух высказываний в одно с помощью союза «или» называется…

6. Константа, которая обозначается «1» в алгебре логики называется…

По вертикали:

1. Совокупность правил, которым подчиняется процесс мышления.

3. Объяснение нового материала

Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b). 

Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции.

     При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:

     1. инверсия;
     2. конъюнкция;
     3. дизъюнкция;
     4. импликация и эквивалентность.

     Для изменения указанного порядка выполнения логических операций используются круглые скобки.
     Предлагается следующий алгоритм построения таблицы истинности.

     1. Определить количество наборов входных переменных - всевозможных сочетаний значений переменных, входящих в выражения, по формуле: Q=2ⁿ , где n - количество входных переменных. Оно определяет количество строк таблицы.

     2. Внести в таблицу все наборы входных переменных.

     3. Определить количество логических операций и последовательность их выполнения.

     4. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.

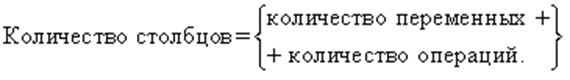
Чтобы не повторить или не пропустить ни одного возможного сочетания значений входных переменных, следует пользоваться одним из предлагаемых ниже способов заполнения таблицы.

     Способ 1. Каждый набор значений исходных переменных есть код числа в двоичной системе счисления, причем количество разрядов числа равно количеству входных переменных. Первый набор - число 0. Прибавляя к текущему числу каждый раз по 1, получаем очередной набор. Последний набор - максимальное значение двоичного числа для данной длины кода.

     Например, для функции от трех переменных последовательность наборов состоит из чисел:

000

001

010

011

100

101

110

111

Способ 2. Для функции от трех переменных последовательность данных можно получить следующим путем:

     а) разделить колонку значений первой переменной пополам и заполнить верхнюю половину нулями, нижнюю половину единицами;

     б) в следующей колонке для второй переменной половинку снова разделить пополам и заполнить группами нулей и единиц; аналогично заполнить вторую половинку;

     в) так делать до тех пор, пока группы нулей и единиц не будут состоять из одного символа.

     Способ 3. Воспользоваться известной таблицей истинности для двух аргументов. Добавляя третий аргумент, сначала записать первые 4 строки таблицы, сочетая их со значением третьего аргумента, равным 0, а затем еще раз записать эти же 4 строки, но теперь уже со значением третьего аргумента, равным 1. В результате в таблице для трех аргументов окажется 8 строк:

000

010

100

110

001

011

101

111

4. Закрепление изученного материала

1. Определить количество строк и столбцов для следующе функции

(Количество входных переменных в заданном выражении равно трем (A,B,C). Значит, количество входных наборов Q=2³=8. Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C, промежуточных результатов  и (B V C), а также искомого окончательного значения сложного арифметического выражения . Соответственно количество столбцов – 6)

2. Начертить таблицу и заполнить заголовок

3. Заполнить таблицу

A

B

C

B V C

0

0

0

1

0

0

0

0

1

1

1

1

0

1

0

1

1

1

0

1

1

1

1

1

1

0

0

0

0

0

1

0

1

0

1

0

1

1

0

0

1

0

1

1

1

0

1

0

5. Выполнение практической работы

Построить для следующих функций таблицы истинности в MS Excel

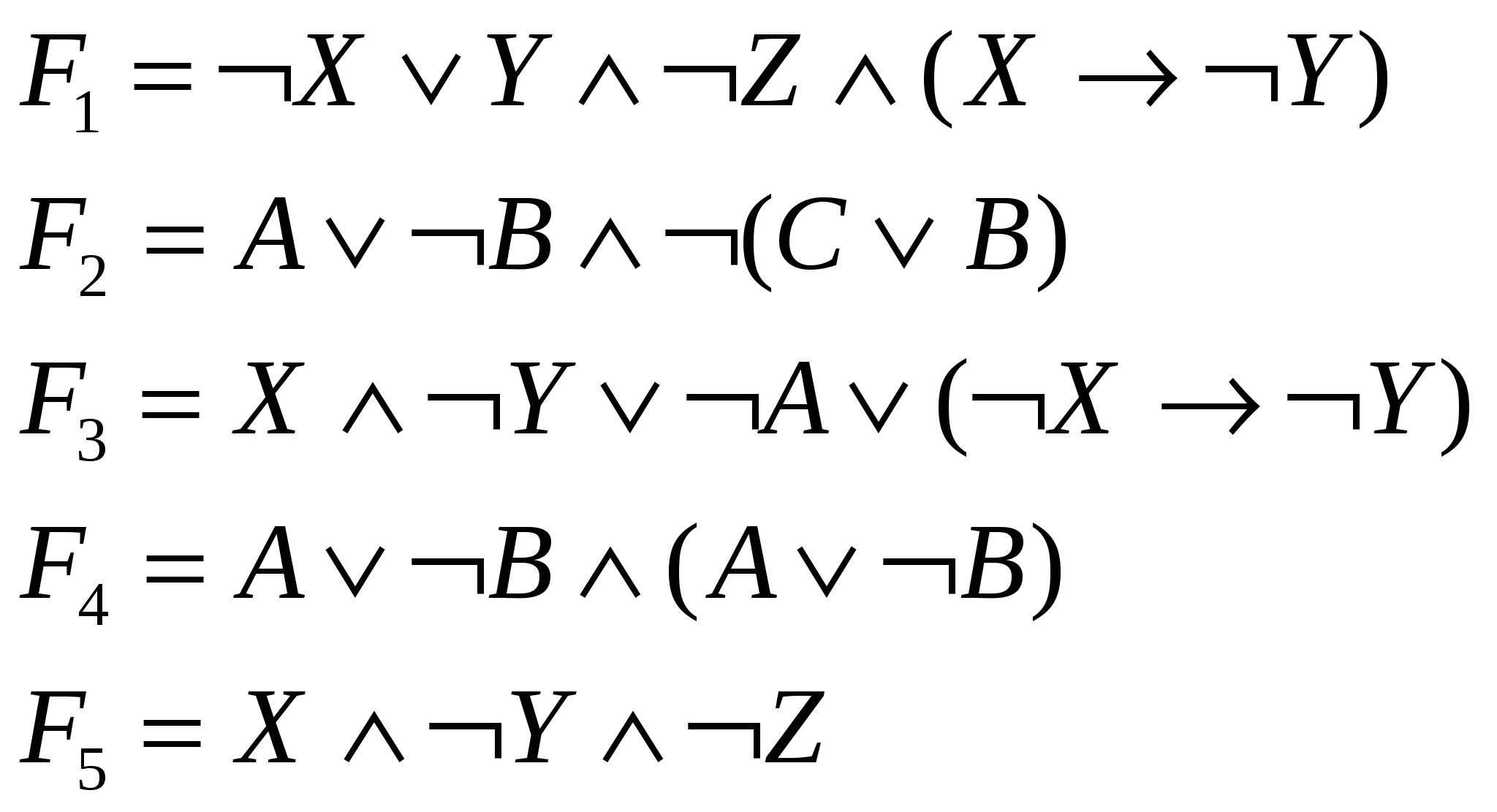
Для ввода логических функций воспользоваться командой [Вставка-Функция или использовать Мастер функций].

Переименовать лист Лист1 в Таблицу истинности и сохранить в файле TabIst.xlc

6. Постановка домашнего задания

Составьте таблицы истинности для функций:

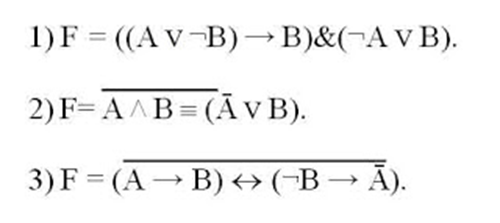
7. Подведение итогов урока

Оценка знаний учащихся по новой теме с учётом повторения материала прошлого урока.

Литература

1. Семакин И.Г. Информатика и ИКТ: учебник для 10-11 классов – М.: Бином. Лаборатория знаний, 2008.

2. Семакин И.Г., Хеннер Е.К. Информатика и ИКТ. Задачник-практикум. Ч. 1, 2. – М.: Бином. Лаборатория знаний, 2009