Конспект открытого урока по математике по теме «Решение показательных уравнений и неравенств» 11 класс
Муниципальное бюджетное общеобразовательное учреждение
«Новомихайловская средняя общеобразовательная школа»
Татарского района Новосибирской области
Конспект урока по математике
в 11 классе
«Решение показательных уравнений и неравенств»
подготовила
учитель математики
Железнова Людмила Михайловна
С. Новомихайловка
2013
Открытый урок в 11 классе.
Тема урока: «Решение показательных уравнений и неравенств».
Цели урока:
образовательные: формирование умений и навыков решать показательные уравнения и неравенства; формирование заинтересованности учащихся в решении показательных уравнений и неравенств при подготовке к ЕГЭ.
развивающие: активизация познавательной деятельности; развитие навыков самоконтроля и самооценки, самоанализа своей деятельности.
воспитательные: формирование умений работать самостоятельно; принимать решение и делать выводы; воспитание устремлённости к самообразованию и самосовершенствованию; осознание учащимися социальной практической значимости учебного материала по изучаемой теме.
Тип урока: урок закрепление знаний. Форма урока: урок-практикум
Ход урока
I Организационный момент.
Сообщение учителем целей, задач и структуры урока, его основных моментов.
II Повторение. Актуализация знаний.
Французский писатель 19 века Анатоль Франс однажды заметил. «Учиться можно только весело…
Чтобы переваривать знания, надо поглощать их с аппетитом».
Совсем скоро вам предстоит сдавать экзамены в форме ЕГЭ. И тема, которую мы изучаем, присутствует в заданиях ЕГЭ. Итак, тема нашего урока «Решение показательных уравнений и неравенств».
Сегодня мы с вами должны обобщить и закрепить умения и навыки решения показательных уравнений и неравенств.
Прежде, чем перейти к устному счету, пойти к доске, решить уравнение.
1)3•16х +2•81х=5•36х. Ответ: х=0,5; х=0.
2) На доске записаны пары уравнений. Устно решить их, из корней составить координаты точки, затем эту точку отметить на координатной плоскости и последовательно соединить получившиеся точки.
1) 5х=625; 2у=32.
2) 5х-2=1; 6у-3=36.
3) 3х-4=1/9; 3у=27.
4) 5х-2=25; 5-у=1/125.
5) 3х-1=27; 2-у=1/2.
6) 14х=196; 5у+2=125.
Пока ребята выполняют задания у доски, мы с вами вспомним теоретический материал, необходимый при решении показательных уравнений и неравенств.
Устный счёт дифференцированный, предлагаю задания разного уровня сложности и оцениваться они будут по-разному.
Лёгкие вопросы оцениваются жетонами зелёного цвета в 1 балл.
Посложнее вопросы оцениваются жёлтыми жетонами в 2 балла.
«Интересные» вопросы оцениваются красными жетонами в 3 балла.
На прошлом уроке мы с вами решали показательные уравнения и неравенства.
Итак, первый вопрос в 1 балл.
Какое уравнение называют показательным? - Уравнение, содержащее переменную в показателе степени, называют показательным.
Какое из предложенных уравнений является показательным? 1) х3=27; 2) 3•х=27; 3) 3х=27.
Как называются уравнения 1) и 2)?
Исключите лишнее уравнение.
1)3х 2-х=1; 2) √3х =9; 3) х3= 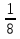 .
.
Почему вы исключили 3)?
Как называются уравнения 1) и 2)?
Какие методы решения показательных уравнений вы знаете?
Графический
Уравнивание показателей
Введение новой переменной
Вынесение общего множителя
Вопросы, оцениваемые в 2 балла:
Указать метод решения показательного уравнения:
53х-1=0,2.
Указать метод решения показательного уравнения:
4х-7•2х+1-32=0.
Решить уравнение: 2х-2=-2.
Решить неравенство:
22х-9<1.
Каким правилом вы пользовались при решении неравенств?
Решить неравенство:
2х > 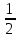 .
.
Решить неравенство:
0,3х ≤0,1.
Вопросы, оцениваемые в 3 балла:
Сколько корней имеет уравнение?
5х = 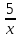
Решить уравнение:
5 1-│х│=25.
Подсчет баллов по жетонам. Проверка работ у доски. Определить лучшего из «Считалочкиных» и задать домашнее задание.
Домашнее задание: стр.299, № 171(а, б), №172 (в,г) + карточка с заданием ЕГЭ.
III Закрепление.
Приобретать знания - храбрость
Приумножать их – мудрость
А умело применять – великое искусство.
Ребята, вы смогли выполнить задания устно, а теперь свои знания необходимо применить при выполнении письменной работы в группах.
Групповая работа. Работаем по группам в парах, как сидите. При выполнении заданий вы можете общаться в группе. Карточки для групповой работы трех уровней сложности: на «3», на «4», на «5».
После выполнения групповой работы каждый учащийся выбирает карточку для индивидуальной работы. Карточки для индивидуальной работы также трех уровней сложности: на «3», на «4», на «5».
Групповая работа.
«3»
3х 2-х=9;
2х-1+2х+2=36;
25х+ 2•5х-3=0;
51-2х >
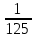 ;
;(
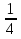 )х2+3х ≤16.
)х2+3х ≤16.
«4»
2х+2 +2х=5;
9х-6•3х-27=0;
22-х -2х-1 =1;
4х - 2 > 0
1-3х
5. Решить систему уравнений: 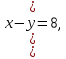
2 х-3у = 16.
«5»
9х-2•3х=63;
5х –(
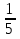 )х-1 =4;
)х-1 =4;Решить систему уравнений:
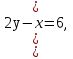
92х+у=32-3у.
4. (0,1) х-1000
2•х-3 > 0
5. 7•49х+5•14х=2•4х
Индивидуальная работа.
«3»
2х 2-3х =
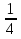 ;
;5х-5х-2 = 600;
9х+3•3х -4 = 0;
73-х <
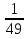 ;
;(
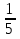 )2х2 -3х ≥5.
)2х2 -3х ≥5.
«4»
3х+2 + 3х = 30;
4х-14•2х -32 = 0;
31-х -3х = 2;
2х – 1
3•х + 2< 0
Решить систему уравнений:
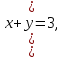
5 х+3у = 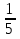 .
.
«5»
4х -3•2х = 40;
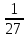 • 3х+2 + 32-х = 4;
• 3х+2 + 32-х = 4;Решить систему уравнений:
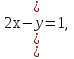
3у/27 =(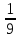 )х-2.
)х-2.
4. (0,2) х-125
3х – 1 > 0
5. 3•9х = 2•15х + 5•25х.
Задания на карточках ЕГЭ:
Найдите наибольшее целое решение неравенства:
(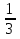 )х ≥ х+4.
)х ≥ х+4.
Найдите область значений функции:
а) у = 2cos x;
б) у = 3sin x .
Решить систему уравнений:
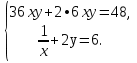
Найдите значение выражения: 3х ( 3х -3), если 3х + 3–х =3.
IV Итог урока: выставить отметки, оценить работу каждого.
Какие уравнения вы сегодня решали?
Какие методы решения показательных уравнений вы знаете?
Чему вы научились сегодня на уроке?
Пригодятся ли вам в будущем умения решать показательные уравнения и неравенства?
Чувствовали ли вы себя комфортно на уроке?
Понравился ли вам сегодня урок?
Какую я себе поставил оценку за урок?
Что я знаю очень хорошо?
Что мне надо подучить?
Спасибо за урок!
Список использованной литературы
Гусев В.А., Мордкович А.Г. Математика. Справочные материалы. Книга для учащихся. – М.: Просвещение, 1988.
Ивлев Б.М. Дидактические материалы по алгебре и началам анализа для 10 класса/ Б.И. Ивлев, С.М. Саакян, С.И. Шварцбурд.
– М.: Просвещение, 2004.
Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/ авторы-составители: И.Р. Высоцкий, Д.Д.Гущин, П.И. Захаров и другие; под редакцией А.Л. Семенова, И.В. Ященко. – М.: АСТ: Астрель,2010.
Фарков А.В. Математические олимпиады в школе 5-11 классы. – М.: Айрис-пресс, 2005.
Фарков А.В. Готовимся к олимпиадам по математике. Учебно- методическое пособие. – М.Издательство «Экзамен», 2006.
Алгебра и начала анализа. Учебник для 10-11 класса средней школы./А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницин и другие: под редакцией А.Н. Колмогорова. – М.: Просвещение, 2006.
Корянов А. Г., Прокофьев А. А. «Математика ЕГЭ – 2013 (типовые задания С – 3) . Методы решения неравенств с одной переменной»
Шестаков С. А., Захаров П. И. «Математика задача С – 1,3».

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ