Конспект урока по математике "Логарифмы"
Урок обобщающего повторения по теме: «Логарифмы».
Цели урока:
Образовательные: проверить сформированность вычислительных навыков учащихся, их умения применять свои знания при решении задач, обобщить и систематизировать знания учащихся, упражнять в решении логарифмических уравнений и неравенств,
Развивающие: развивать аналитическое мышление, произвольное внимание, память учащихся; создать реальные условия для индивидуального дифференцированного подхода в обучении.
Воспитательные: воспитывать у учащихся умение работать в группе, умение выражать свою мысль, формировать у учащихся «здоровое» соперничество, формировать интерес и любовь к математике.
Оборудование урока:
Плакат: « Найди ошибку»
Сигнальные карточки с числами.
Тексты с тестами на каждую парту.
Плакат с шифром.
Карточки с заданиями.
Запись на доске заданий по выбору.
Кодированные карточки каждому.
Плакат для кодированного задания.
Ход урока
1. Организационный момент.
Сообщение цели урока
2. Устный счет.
Весь класс работает с сигнальными карточками.
log121 11 1.
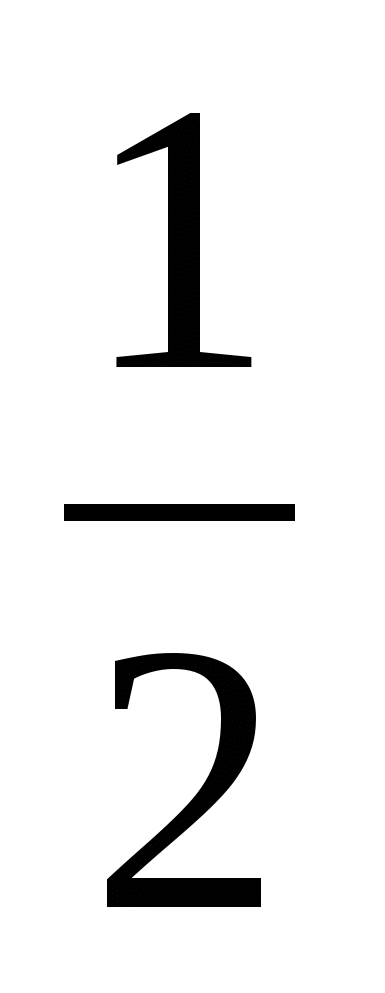
logо.1
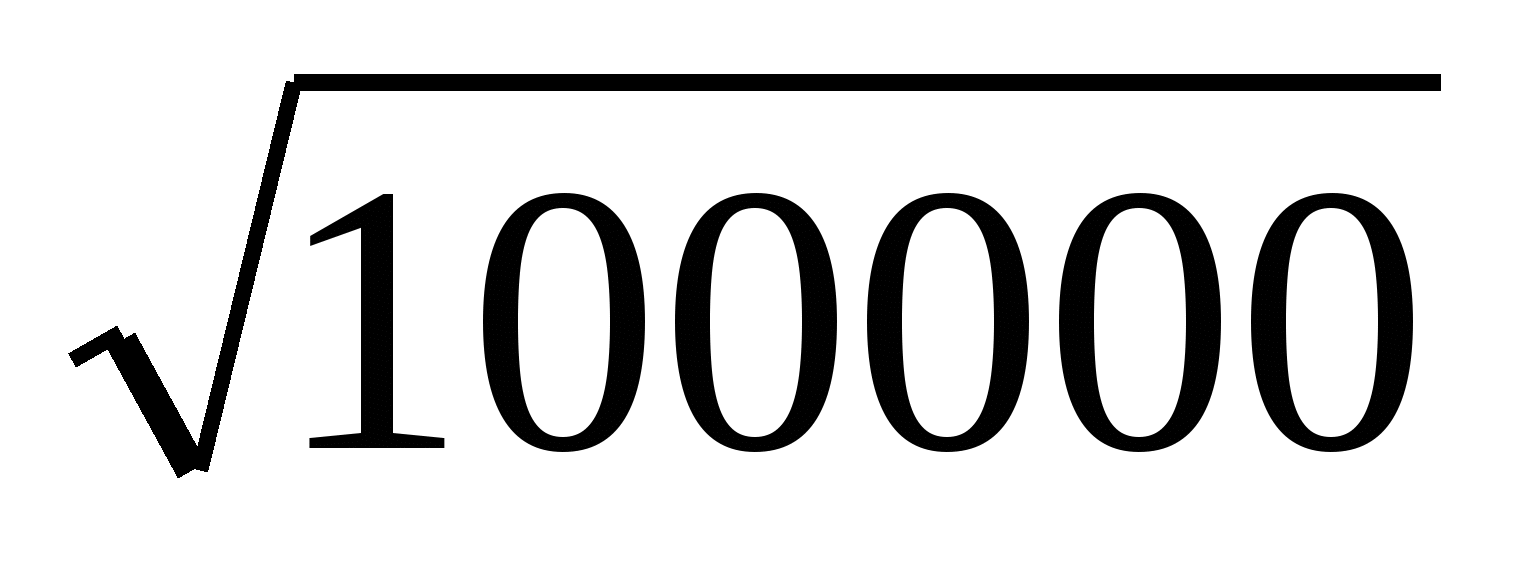 2. -2,5
2. -2,5log2 10 - log2 5 + Log2 8 3. 4
log2
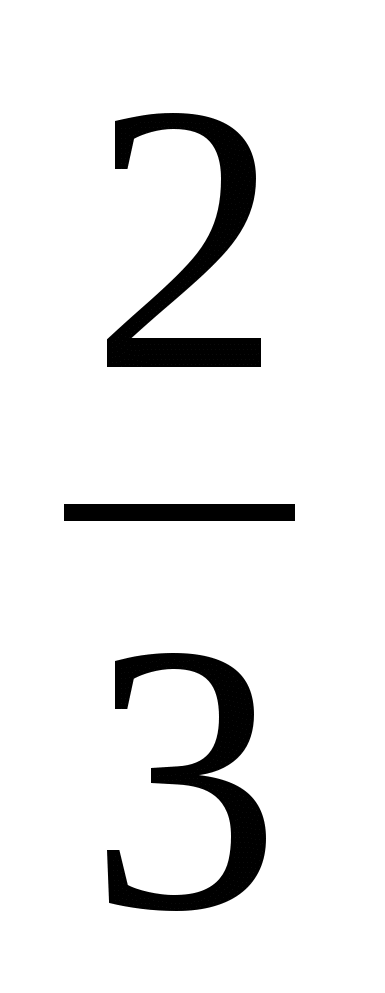 + log4
+ log4 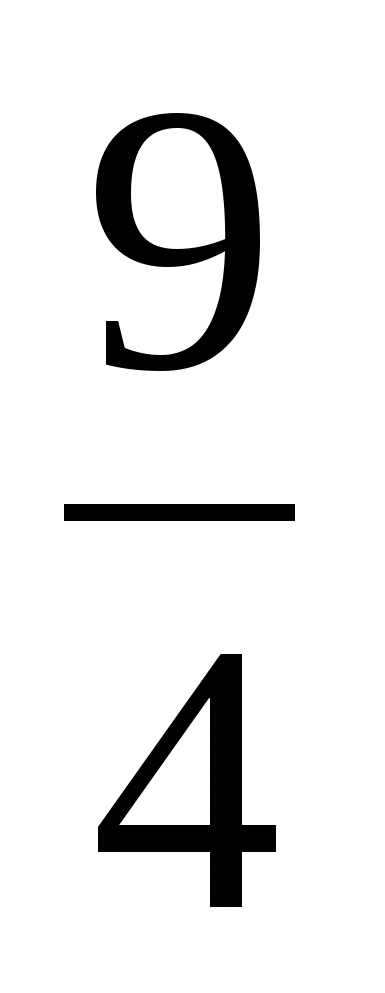 4. 0
4. 0log36 16 + 2 Log6 3 5. 2
32log327 6. 27
52+log
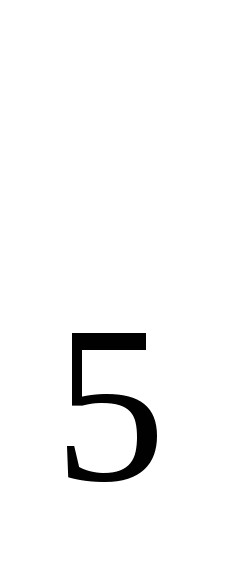 3 7. 125
3 7. 125log2 log3 81 8. 2
log11
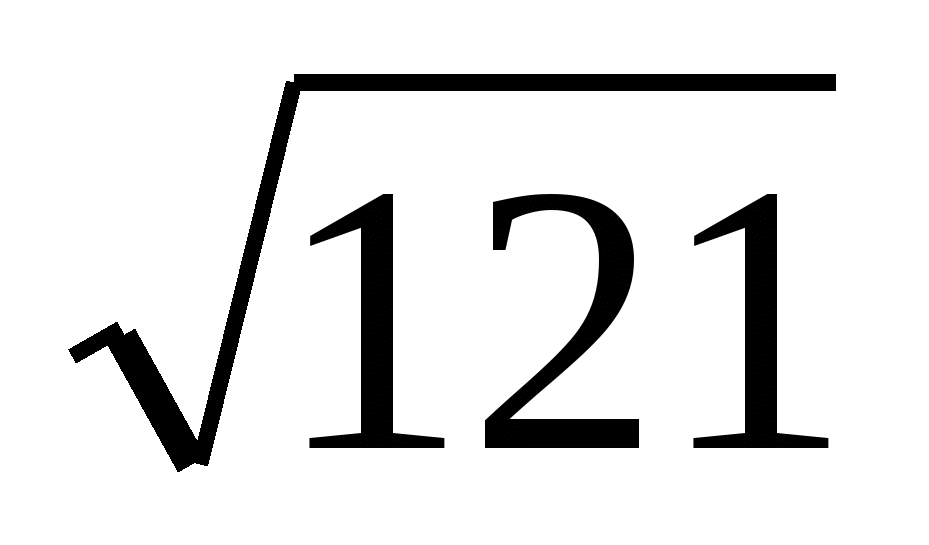 9.
9.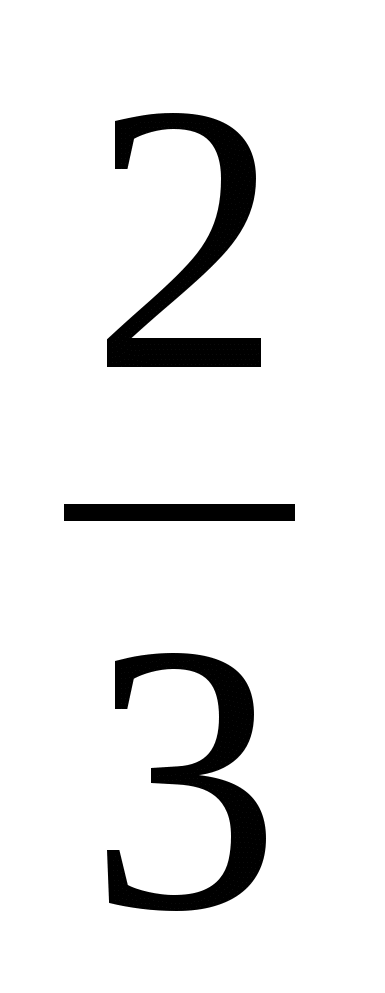
log3 3 –
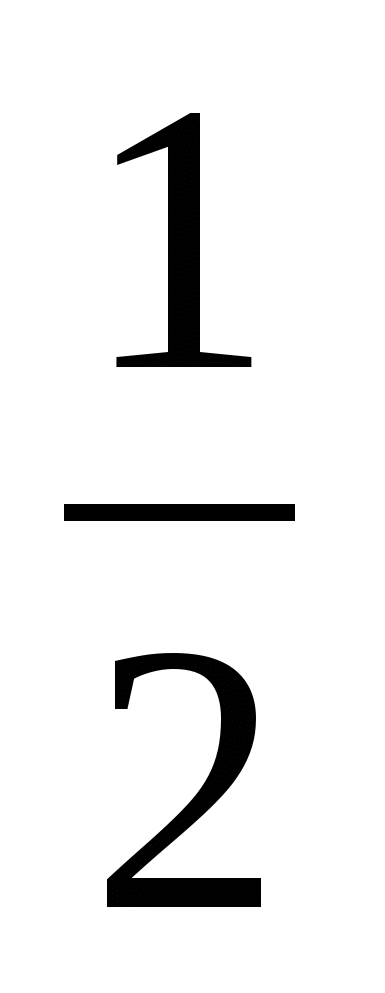 log3 9 10. 0
log3 9 10. 0
3. Найдите ошибку в рассуждениях ( на плакате).
![]() >
> ![]()
lg ![]() > lg
> lg ![]()
2lg ![]() > 3lg
> 3lg ![]()
> 3
ОТВЕТ: т.к. lg![]() <0 , то при делении на отрицательное число, знак неравенства меняется, значит , 2 <3.
<0 , то при делении на отрицательное число, знак неравенства меняется, значит , 2 <3.
4. Тест.
При каких значениях х выражения имеют смысл:
Вариант1
Вариант2
А
Б
В
Г
log5 (7 – х)
log5 ( х – 7 )
x > 7
0< х< 7
x < 7
x ![]() 7
7
log2 ( 9 – х2 )
log3 (х2 – 16 )
x < –3,
x > 3
x < –4,
x >4
-3< x< 3
-4< x< 4
log4 ![]()
log4 ![]()
x < –2,
x > 5
x > –5,
x < –2
–1< x < 6
–2< x< 5
log3 (х2 – 4х + 4)
log7 (х2 - 6 + 9)
-2<х< 2
x ![]() R
R
x![]() 2
2
x >3
x ![]() R
R
x ![]() 3
3
Ответы:1в. ВВГБ;
2в. АБВГ.
5. Отгадайте фразу.
На доске записано высказывание Г.Галилея, которое вы должны прочитать. Оно зашифровано. На доске в строчку записан ряд чисел от 1 до 44; под каждым числом пишите букву, и таким образом получится фраза.
Плакат с шифром.
А
В
Д
Е
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Ы
Я
![]()
![]()
200
![]()
![]()
-5
10
25
24
9
![]()
![]()
2
![]()
3
-2
1
40
8
Ученики получают по 2-3 карточки с заданиями ( подхожу к раздаче дифференцировано).Выполнив задание, ищут в таблице букву, которой соответствует ответ и записывают ее на доске под номером карточки.
Карточки: Ответы:
1). Вычислите![]() 3/5
3/5
2).Решите уравнение: log3 (3x – 5) = log3 (2x – 3) 2
3).Вычислите: log3![]() - 5
- 5
4). Вычислите: ![]() 2
2
5). Вычислите: 2 log2 ![]()
![]()
6) Вычислите: ![]() 200
200
7). Вычислить: ![]()
![]()
8). Вычислите: ![]() log 2 log2 16 1
log 2 log2 16 1
9). Вычислите: ![]() log9 log2 8
log9 log2 8 ![]()
10).Решите уравнение: ![]() (6x – 4) = -3 2
(6x – 4) = -3 2
11). Вычислите: 24 log2 log2 log2 16 24
12). Вычислит : log0.5 4 -2
13). Вычислите:![]() 25
25
14).Решите уравнение: 3lg 2 +lg( x + 8) =lg 48 - lg2 -5 15).Вычислите: lg 20 + lg5 2
16).Решите уравнение: log2 (x+6)= 2 - 2
17).Решите уравнение: log2![]() = x
= x ![]()
18).Решите уравнение: x =log5 125 3
19).Решите уравнение: log0.045 = x - ![]()
20).Вычислите: ![]() -
-![]()
21).Решите уравнение: log2 (x+![]() ) = - 1
) = - 1 ![]()
22).Решите уравнение: lg 40 – lg2 = lg (10 -2 x) - 5
23). Вычислите: ![]()
![]()
24).Решите уравнение: log5 x = -2 ![]()
25).Решите уравнение: lg(9x + 10) =2 10
26). Вычислите: ![]()
![]()
27). Вычислите: ![]() 9
9
28). Вычислите: ![]() 40
40
8
29). Вычислите: ![]()
30 ). Вычислите: ![]()
![]()
31). Вычислите:![]()
![]()
![]() 40
40
32). Вычислите: ![]() 10 33).Вычислите:
10 33).Вычислите: ![]()
![]()
34).Решите уравнение: log7 (2 x + 1) = 2 24
35). Вычислите: ![]() 24
24
36).Решите уравнение: log3 (8 ![]() + x ) = 2
+ x ) = 2 ![]()
37).Вычислите: lg 3000 – lg3 3 38). Вычислите:![]()
![]()
39 ). Вычислите: (log2 4)3 ![]() log3 27 24
log3 27 24
40).Вычислите: ![]()
![]()
41).Решите уравнение: log5 (2 x - 1) = 1 3 42).Решите уравнение: lg 2 +lg(2- x) = lg(19- x) - 5
43 ). Вычислите: 2lg ( 100000) 10
44).Решите уравнение: log3 (6–3x)= log3 (26+x) - 5
Ответ: «Природа формулирует свои законы языком математики».
6. Программированный контроль
Задание
ответ
Вариант №1
Вариант№2
1
2
3
4
Решите уравнение
log0,5 (![]() - 1) = - 1
- 1) = - 1
log0,2 (6 – ![]() ) = 1
) = 1
1
5
8
9
lg 2x - lg x= 0
lg 2x + lg x= 0
1; 100
1; 0,1
1; 10
1; 0,01
Решите неравенство
x < 0
-1 < x < 0
x > 0
x < -1
log5 ( - x ) < 0
log0,4 ( - x ) < 0
Ответ: 1 вариант: 432;
2 вариант: 124
7. Задание по выбору.
Решите уравнение:
Уровень 1 : log2 (x +3) =4 Ответ: 13
Уровень 2: log9 x +2 log3 x= 5 Ответ: 9
Уровень 3: Найти наибольший корень уравнения
lg ( x +6) – 2 = ![]() lg(2x - 3 ) -lg 25 Ответ: 14
lg(2x - 3 ) -lg 25 Ответ: 14
8.Кодированные карточки. (ученики получают карточки, на доске -задание. Ученик выбирает правильный ответ и ставит «*».
1
2
3
4
1
2
3
4
5
Задание на доске.
1
2
3
4
1.Найти область определения
y = ![]()
x > ![]()
x <![]()
x < - ![]()
x > - ![]()
2. Решите уравнение
x = log27 ![]()
Нет решений
x = ![]()
х = -![]()
x = 81
3. lg( 2 x +1) = lg x
x = 1
Нет решений
х= -1
х=0
4.lg x2 = 0
x =![]() 1
1
x = - 1
х= 1
Нет решений
5. Какое число лишнее?
log3 0,7
![]() 12
12
log0,5 ![]()
![]()
log0,3 27
Ответ:
1
2
3
4
1
*
2
*
3
*
4
*
5
*
9. Итог урока.
10. Учащимся выставляется оценка за урок.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ