Государственное областное бюджетное

профессиональное образовательное учреждение

«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»

Методическая разработка

урока математики

на тему

«МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ».

Выполнил:

преподаватель математики

первой квалификационной категории

Заварзина В.Г.

Липецк 2014 г.

Тема урока:

«Методы решения тригонометрических уравнений».

Цели урока:

1. Образовательные:

а) закрепить навыки решения тригонометрических уравнений;

б) обобщить знания студентов о методах решения тригонометрических уравнений;

в) сформировать умения и навыки в правильном выборе метода решения тригонометрических уравнений.

г) расширить знания и умения студентов, связанные и применением методов решения тригонометрических уравнений.

2. Развивающие:

а) развитию математического мышления студентов

б) развитие умений студентов: наблюдать, сравнивать, обобщать, классифицировать).

3. Воспитательные:

а) воспитание навыков самостоятельной работы;

б) воспитание дисциплинированности;

в) побуждать в студентах стремление к преодолению трудностей в процессе умственной деятельности.

Тип урока: комбинированный

Вид урока: проблемный

Методические приемы:

-самостоятельная работа (работа с раздаточным материалом);

-практический- решение задач.

Межпредметные связи: история

Оборудование и наглядные средства обучения: мультимедийный проектор, интерактивная доска, презентация, демонстрационный и раздаточный материал, задачник “Алгебра и начала математического анализа” (профильный уровень часть 2) под редакцией А. Г. Мордковича .

Методическая цель: активизировать мыслительную деятельность студентов.

Ход урока:

I.Организационный момент: Подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей)

II. Сообщение темы и целей урока.(слайд 1,2)

«Метод решения хорош тем, если с самого начала мы можем предвидеть – и в последствии подтвердить это, - что, следуя этому, мы достигнем цели»

Лейбниц .

На этом уроке мы поговорим о методах решения тригонометрических уравнений. Мы знаем, что правильно выбранный метод часто позволяет существенно упростить решение, поэтому все изученные методы нужно помнить, чтобы решать конкретные задачи наиболее подходящим методом.

Давайте сегодня на уроке будем активны и внимательны, будем работатьс большим желанием, ведь все эти знания пригодятся вам в дальнейшей жизни.

Ш. Проверка домашнего задания.

1.Вам на дом было задано решить уравнение:

(Предварительное домашнее задание:решить уравнение:

. Отмечаем, что в уравнении a,b,c любые действительные числа).

Давайте проверим его решение на доске.

Поднимите руки, кто хочет выйти к доске написать и объяснить решение уравнения?

Студент выходит к доске и пишет решение.

Выразим , и 1 через функции половинного аргумента:

:

,

, или

,

,

Ответ: ,; ,, .

Каким методом решили это уравнение?

Метод сведения уравнения к однородному уравнению.

В чём заключается этот метод?

Студент :

Используя формулы двойного угла и основное тригонометрическое тождество, приводим данное уравнение к половинному аргументу.

2. Одному из студентов было задано сделать сообщение о методах тригонометрических уравнений.

Студент выходит к доске и делает сообщение.

В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд».

Слово «тригонометрия» впервые встречается в 1505 г. в заглавии книги немецкого теолога и математика Бартоломеуса Питискуса (Bartholomäus Pitiscus, 1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.

Происхождение этого слова греческое: τρίγωνον — треугольник, μετρεω — мера. Иными словами, тригонометрия — наука об измерениях треугольников. Возникновение тригономет-рии связано с землемерением, астрономией и строительным делом. Хотя название возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны уже 2000 лет назад

Длительную историю имеет понятие синуса. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в 3 в. до н.э. в работах великих математиков Древней Греции — Евклида, Архимеда, Аполлония Пергского. В римский период эти отношения уже достаточно систематично иследовались Менелаем (Iв. н. э.), хотя и не приобрели специального названия. Современный синус угла α, например, изучается как полухорда, на которую опирается центральный угол величиной α, или как хорда удвоенной дуги.

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

В настоящее время изучению тригонометрических функций и тригонометрических уравнений уделяется большое внимание в школьном курсе алгебры и начал анализа.

Преподаватель : давайте посмотрим на доску (слайд3,4)

IV. Мотивация

Ребята! Давайте посмотрим на доску.(слайд5)

Примеры:

1. 2cos (x/2) – 5sin (x/2) – 5 = 0.

2. cos 2x + cos2 x = 5/4.

3. sin x + sin 2x + sin 3x = 0.

Перед нами уравнения, которые мы пока что решить не можем, но сегодня на уроке мы познакомимся с некоторыми методами решения тригонометрических уравнений. Давайте сначала повтори как решаются простые тригонометрические уравнения .

V.Актуализация опорных знаний

Давайте вспомним формулы для решения тригонометрических уравнений.(слайд 6)

Ребята расскажите по каким формулам мы будем находить корни уравнений.

Давайте вспомним частные случаи для нахождения корней уравнений (слайд7)

Проведём небольшую работу по карточкам в двух вариантах и повторим основные формулы.

Ребята решают задания по карточкам. Потом они меняются вариантами и проверяют решения с правильными на обратной стороне доски. Ставят + или – напротив заданий и сдают преподавателю.

Задание 1 :решите уравнения.

1 Вариант

1.

2.

3.

4.

5.

6.

2 Вариант

1.

2.

3.

4.

5.

6.

Ответы:

1 Вариант

1)

2)

3)

4)

5)

6)

2 Вариант

1)

2)

3)

4)

5)

6)

VI Ведение нового материала

Сегодня на уроке мы с вами рассмотрим три метода решения тригонометрических уравнений.

I Метод замены переменной(слайд8)

Давайте посмотрим на доску.

На слайде описана схема решения уравнений методом замены переменной. Давайте рассмотрим в чём он заключается.

С этим методом вы знакомы со школы.

Схема решения:

Шаг 1. Привести уравнение к алгебраическому виду относительно одной из тригонометрических функций.

Шаг 2. Обозначить полученную функцию переменной t (если необходимо, ввести ограничения на t).

Шаг 3. Записать и решить полученное алгебраическое уравнение.

Шаг 4. Сделать обратную замену.

Шаг 5. Решить простейшее тригонометрическое уравнение.

Давайте решим наше первое уравнение по этому методу.

Ребята, кто хочет выйти попробовать решить данное уравнение?

Студент выходит к доске.

Пример.

2cos (x/2) – 5sin (x/2) – 5 = 0.

Решение.

1) 2(1 – sin (x/2)) – 5sin (x/2) – 5 = 0;

2sin (x/2) + 5sin (x/2) + 3 = 0.

2) Пусть sin (x/2) = t, где |t| ≤ 1.

3) 2t + 5t + 3 = 0;

t = 1 или t = -3/2, не удовлетворяет условию |t| ≤ 1.

4) sin (x/2) = 1.

5) x/2 = π/2 + 2πn, n Є Z;

x = π + 4πn, n Є Z.

Ответ: x = π + 4πn, n Є Z.

II. Метод понижения порядка уравнения

Давайте посмотрим на доску(слайд9).

На слайде описана схема решения уравнений методом понижения порядка уравнения. Давайте рассмотрим в чём он заключается.

Схема решения

Шаг 1. Заменить данное уравнение линейным, используя для этого формулы понижения степени:

sin2 x = 1/2 · (1 – cos 2x);

cos2 x = 1/2 · (1 + cos 2x);

tg2 x = (1 – cos 2x) / (1 + cos 2x).

Шаг 2. Решить полученное уравнение с помощью методов I и II.

Давайте решим наше уравнение по этому методу.

Ребята, кто хочет выйти попробовать решить данное уравнение?

Студент выходит к доске.

Пример.

cos 2x + cos2 x = 5/4.

Решение.

1) cos 2x + 1/2 · (1 + cos 2x) = 5/4.

2) cos 2x + 1/2 + 1/2 · cos 2x = 5/4;

3/2 · cos 2x = 3/4;

cos 2x = 1/2;

2x = ±π/3 + 2πn, n Є Z;

x = ±π/6 + πn, n Є Z.

Ответ: x = ±π/6 + πn, n Є Z.

III. Метод преобразования уравнения с помощью тригонометрических формул

Давайте посмотрим на доску.( слайд10)

На слайде описана схема решения уравнений методом преобразования уравнения с помощью тригонометрических формул Давайте рассмотрим в чём он заключается.

Схема решения

Шаг 1. Используя всевозможные тригонометрические формулы, привести данное уравнение к уравнению, решаемому методами I, II, III, IV.

Шаг 2. Решить полученное уравнение известными методами.

Пример.

sin x + sin 2x + sin 3x = 0.

Решение.

1) (sin x + sin 3x) + sin 2x = 0;

2sin 2x · cos x + sin 2x = 0.

2) sin 2x · (2cos x + 1) = 0;

sin 2x = 0 или 2cos x + 1 = 0;

Из первого уравнения 2x = π/2 + πn, n Є Z; из второго уравнения cos x = -1/2.

Имеем х = π/4 + πn/2, n Є Z; из второго уравнения x = ±(π – π/3) + 2πk, k Є Z.

В итоге х = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.

Ответ: х = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.

Теперь мы смогли решить уравнения.

VII Закрепление нового материала

Решение задач.

Давайте решим у доски следующие примеры:

Задание 2

1. 6sin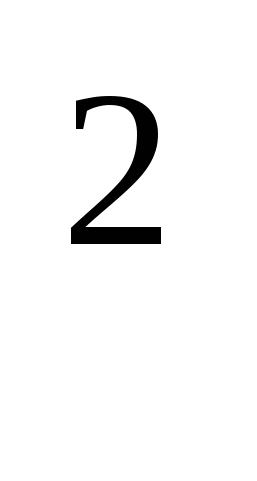x−5sinx+1=0

2)sin5x + sinx=0;

3)

Решение уравнений у доски.

Вызываются учащиеся.

1)Каким методом мы решим первое уравнение?

Метод замены переменный и подстановки

Решение:

Как будем решать данное уравнение?

Введем новую переменную sinx=t It11 , получим квадратное уравнение 6t−5t+1=0. Его корнями являются числа t= и t=. Дданное уравнение сводится к простейшим тригонометрическим уравнениям sinx= и sinx=. Решая

их, находим, что x=(−1) и x=(−1)arcsin+nZ корни уравнения.

2)sin5x + sinx=0;

Как будем решать данное уравнение?

Метод преобразования уравнения с помощью тригонометрических формул

Решение. Преобразовав сумму синусов в произведение, получим

Значит sin3x=0, либо , откуда находим , либо cos2x=0, откуда находим:

3)Решить уравнение

Как будем решать данное уравнение?

Метод понижения порядка уравнения.

Решение.

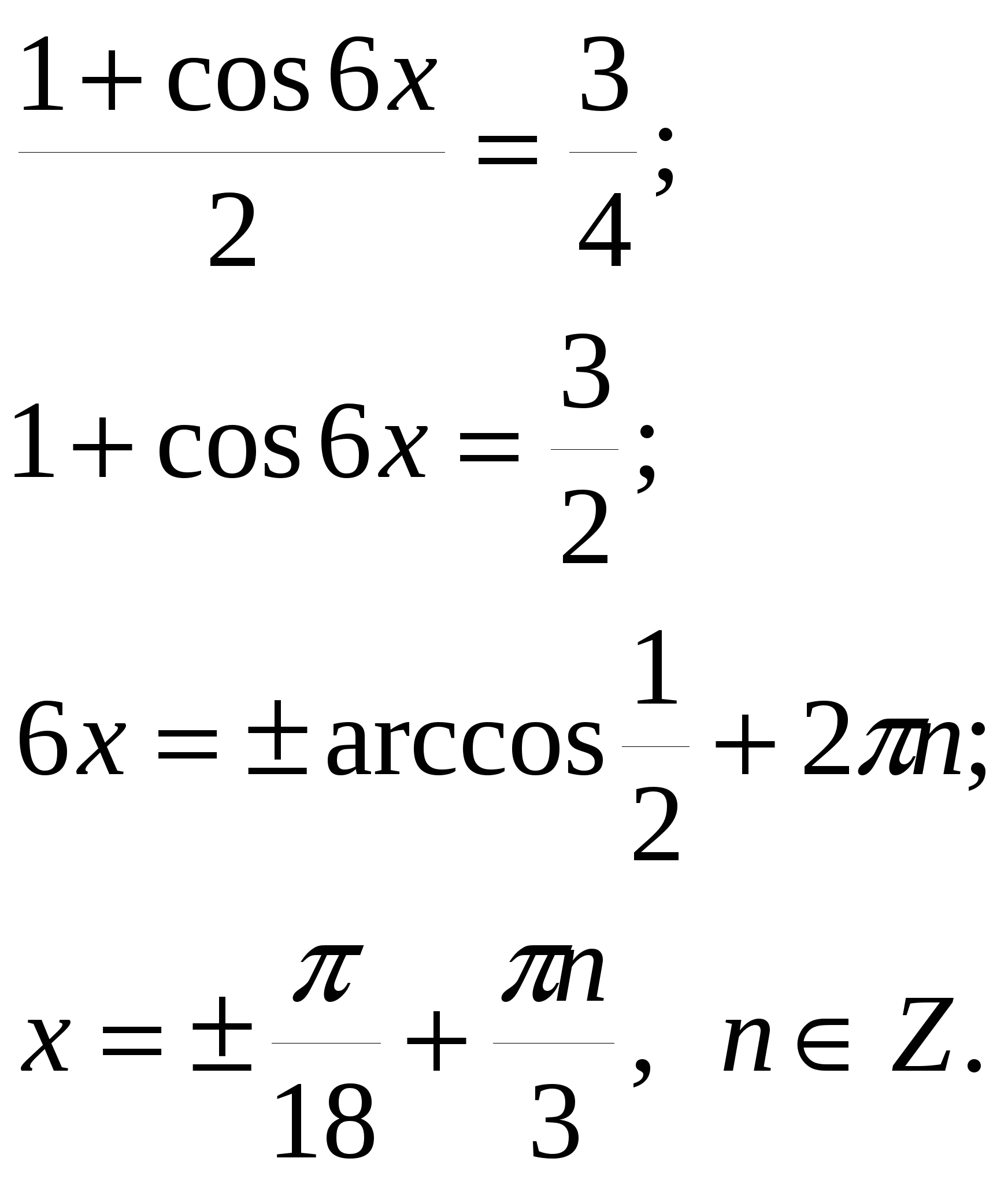
VIII.Подведение итогов урока:

Сегодня на уроке мы повторили формулы для нахождения корней тригонометрических уравнений, решали познакомились с тремя методами решения тригонометрических уравнений, решали уравнения на применение этих методов.

Выставление оценок за урок.

IX.Домашнее задание:

Повторить методы решения уравнений.(слайд 11)

§31 № 31.5 (а,б)

Список литературы:

1. М.И. Башмаков. Алгебра и начала анализа; Учебник для 10-11 кл. средней школы – 2-е изд. – М. Просвещение, 2000.

2. А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын. Алгебра и начала анализа: Учебник для 10-11 кл. средней школы – 4-е изд. – М. Просвещение, 2002

3. Кононов А.Я. «Устные занятия по математике в старших классах» М., Столетие, 1997

4. Мордкович А.Г.и др. Алгебра и начала анализа.10 кл.: В двух частях.Ч.1: Учеб. для общеобразоват. Учреждений(профильный уровень) )/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—7-е изд., стер.—М.: Мнемозина, 2010.

5. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных . учреждений (профильный уровень)/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—7-е изд., стер.—М.: Мнемозина, 2010.