Урок по теме «Обыкновенные дроби»



















Обухова Людмила Николаевна
Сосновский филиал МБОУ «Новопокровская сош», Мордовский район Тамбовская область
Учитель математики
Урок по теме «Обыкновенные дроби».
Цели:
Образовательные: закрепить у учащихся умение выполнять действия сложения и вычитания дробей с одинаковыми знаменателями, учить выделять целую часть из неправильной дроби и наоборот.
Воспитательные: воспитание аккуратности, дисциплины, настойчивости, ответственного отношения к учебе.
Развивающие: развитие памяти, речи, любознательности, познавательного интереса; формирование представлений о соотношении целого и его частей (часть меньше целого), обучение представлению информации в различных видах (иероглифы, смешанное число и неправильная дробь), формирование представлений о математическом языке, его компонентах, историческом развитии.
Ход урока:
Организационный момент
Человек подобен дроби, где числитель - это
то, что он действительно собой представляет,
а знаменатель-то, что он себе воображает. Чем
больше знаменатель, тем меньше дробь. Коль
знаменатель-бесконечность, дробь равна нулю.
Л.Н.Толстой.
Вступительное слово учителя
Не каждый человек может стать великим математиком, но каждый учащийся должен иметь хорошие знания по математике, сегодня мы проводим урок по теме: «Обыкновенные дроби».
II. Работа на уроке.
постановка цели урока;
В самых древних письменных источниках встречались не только натуральные числа, но и дроби. Действия над дробями в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он попал в дробь. Толстой писал: …
Действительно, сегодня мы с вами:
обобщим полученные знания по теме;
выявим результаты владения навыками сложения и вычитания дробей;
закрепим наши знания.
б) устный счёт;
– Ребята, давайте поиграем в игру “Счётная машина”?
Вспомним, какие требования к этой игре мы выработали (1. быстрота;
2. правильность; 3. тишина)
(Ученик, сидящий на последней парте, выполняет первое действие, результат передает человеку, сидящему перед ним, 2 ученик выполняет 2 действие, передает результат следующему и т.д.. Ученик, сидящий на первой парте, выполняет последнее действие, идёт к доске и записывает конечный результат.)
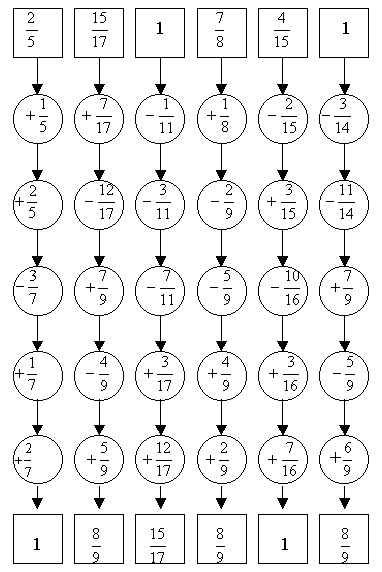
Подведём итоги. Какая машина какое место заняла.
Ребята, сегодня на уроке мы с вами отправимся в необычное путешествие, посетим страну Дроби, узнаем об истории её возникновения.
В путешествии вы должны показать все свои знания о дробях и получить новые исторические сведения.
Вопросы
Учитель: Что такое дробь?
Уч-ся: Дробь- это число, составленное из одинаковых долей единицы.
Учитель: Что показывает знаменатель дроби?
Уч-ся: знаменатель дроби показывает, из каких долей составлена дробь.
Учитель: Что показывает числитель дроби?
Уч-ся: числитель показывает, сколько таких долей взято.
Математический диктант
(2уч-ся выполняют у доски)
Запишите дроби. Подчеркните правильные дроби:
![]()
![]()
1вариант-подчеркнуть правильные дроби
2вариант-подчеркнуть неправильные дроби
2.Запишите и подчеркните дроби, расположенные на луче
правее единицы (1в), левее единицы(2в).
7 18![]()
3. Напишите
1 2
Неправильных дробей с числителем 4
Правильных дробей со знаменателем 5
4. Дополните дроби до 1: 1/3,2/5, 3/10, 7/16,8/9
5.Какую часть составляет
1см от дм
1см от дм
1 см от дм
Самопроверка.
в) Игра “Отгадай слово”
Открыли тетради и записали тему урока “Обыкновенные дроби”.
Сегодня мы постараемся показать свои знания по этой теме. Теоретический материал, который мы с вами изучили, представлен в таблице, в ходе урока можно обращаться за помощью к ней.
Потребовались тысячелетия, прежде чем люди научились делить единицу на части.
Какой древний народ впервые обозначил дроби, мы узнаем, если решим примеры.
А для этого мы поиграем в игру “Отгадай слово”. Вы будете решать примеры, записанные на доске, результат каждого примера связан со следующим примером. Решив 1 пример, вы получаете 1 букву слова,
2 пример – 2 буква. Ответы приведены ниже, вы выбираете и записываете рядом с ним букву.
№1 (комментирование)
2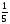 +
+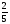 = * 2
= * 2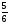 - и; 2
- и; 2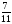 - ч;
- ч;
* + 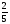 = 2
= 2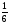 - т; 2 - я; 3
- т; 2 - я; 3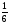 -и
-и
-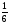 = 2
= 2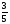 - е; 3 - г;
- е; 3 - г; 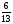 -ь;
-ь;
- 2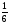 =
= 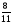 - е; 1 - л; 1
- е; 1 - л; 1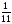 - е;
- е;
+1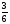 =
= 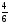 - п; 1
- п; 1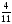 - н
- н
- 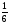 = (слово “египтяне ”)
= (слово “египтяне ”)
- 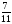 =
=
-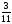 =
=
Для тех, кто справился, задание на доске “В свободную минутку”.
№ 1
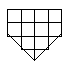 На доске была изображена фигура. Ученик по ошибке стер часть фигуры. Попробуйте восстановить всю фигуру, если известна, что оставшаяся часть составляет
На доске была изображена фигура. Ученик по ошибке стер часть фигуры. Попробуйте восстановить всю фигуру, если известна, что оставшаяся часть составляет 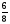 всей фигуры.
всей фигуры.
№ 2
-сказал ученик. Мышка в 6 раз тяжелее слона.
30
5
В чём ошибка?
Учитель: Молодцы! Многие успешно справились и угадали это слово, “египтяне ”.
слайды
Древние египтяне уже знали, как поделить два предмета на троих. Но все остальные дробные числа были единичными дробями, т.е. числитель равен 1
½, 1/3, 1/28 … Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Изучение папирусов показало, что египтяне обозначали дроби так:
см. слайды
Изучение папирусов показало, что египтяне обозначали дроби не так, как мы: вверху – числитель, внизу – знаменатель.
У них черты для дроби не было, специально общего для всех дробей способа обозначения не было.
![]()
У египтян были в ходу специально составленные таблицы, при помощи которых они и производили действия над такими дробями.
Одновременно с единичными дробями в Вавилоне появились системные дроби, знаменатель, которых содержит 60.Например:1с=1/60мин,…Они также называются астрономическими дробями.
см. слайды
Учитель: Из какой страны берёт обозначение дробь, мы узнаем, решив уравнения
№2.Найдите неизвестное число, если: 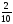 + а = 1; k +
+ а = 1; k + 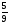 = 1; 1 x =
= 1; 1 x =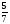
= 9 = 12
2 у
Учитель: Именно в Древней Индии стали
1
3.
В индийской рукописи, написанной около 4 в. н. э. дробь 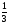 записывалась так
записывалась так
Черта дроби стала использоваться около 300лет назад.
Первым учёным, который ввёл современную запись дроби стал итальянский математик Леонардо Пизанский(Фибоначчи) в 1202г.
Он ввел слово дробь. Запись дробной чертой установилась не сразу. Леонардо Пизанский применяет черту регулярно. После него черта для дроби вошла во всеобщий обиход.
Сын писаря. Был путешественником и купцом.
Иногда ему доводилось решать и такие задачи.
Задача: №3.
На базаре продавали ткань. Утром продали 21 м, что составляет 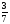 ткани проданной за день. Сколько м ткани продали за день?
ткани проданной за день. Сколько м ткани продали за день?
21:3*7=49(м)-продали всего.
Ответ:49метров.
1. Какой еще вопрос можно поставить к задаче?
(Какую часть ткани не продали? Сколько метров ткани не было продано? Когда ткани продали больше? Почему?)
Давайте составим обратную задачу и решим её.
На базар привезли 49м ткани. Утром продали 3/7 привезённой ткани. Сколько ткани продали утром?
49:7*3=21(м)-продали утром.
Ответ:21 метр
3. Придумайте ещё задачу с такими же данными и сформулируйте её.
Физкультминутка (математическая)
( физические упражнения подобраны с правильными и неправильными ответами в примерах)
Анализ физкультминутки
(Какие математические ошибки допущены)
в) Самостоятельная работа
В 13 веке греческий монах, учёный- математик ввёл названия: знаменатель дроби и числитель.
Его имя вы узнаете, решив самостоятельную работу (по уровням).
Сейчас вы выполните самостоятельную работу с зашифрованными ответами. Выполняйте работу в тетрадях, а мне сдадите на листочках шифр ответов.
1уровнь
1) 5 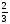 =
=
н
а
л
п
д
у
12
7
4
6
9
3
1
7
11
2) 6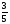 + 2
+ 2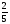 =
=
3) 2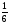
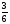 =
=
4) 10 + 2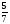 =
=
5) 7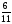 + 2
+ 2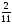 =
=
6 7
6) 1- =
Код (ПЛАНУД)
Максим Плануд ввёл названия: знаменатель дроби и числитель.
III. Итог.
Проверка творческих заданий.
Оценки за урок.
Молодцы! Сегодня на уроке мы совершенствовали свои умения и навыки, применяя порученные знания.
IV. Домашнее задание:
-Ещё раз перенесёмся в глубокую древность на 4 тыс.лет назад в Древний Египет.
Старинная задача.
Приходит пастух с 70 быками. Его спрашивают: сколько приводишь ты из своего многочисленного стада? Пастух отвечает: «Я привожу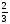 от трети.» Сколько быков было во всём стаде?
от трети.» Сколько быков было во всём стаде?
(Папирус Ахмеса. Египет. 1850г. до н.э.)
(2. Сочинить и записать на листочках сказку об обыкновенных дробях. В сказке вы должны описать те действия, правила, с которыми мы уже знакомы, использовать полученные знания и умения. Можно сопроводить иллюстрациями.)
Русь.
На Руси, как и у других народов, первым учителем математики, дробей была сама жизнь. В 1 тыс. славяне умели разрубать металлическую полосу на равные части.
Дробь в русском языке появилось в 8 веке, происходит от глагола «дробить»- разбивать, ломать на части.
-Наше путешествие по историческим вехам дроби заканчивается.
- Мы с вами уже научились некоторым действиям с дробями. Я, надеюсь, что вы умеете работать с дробями и, у вас не будет возникать при этом особых трудностей.

(Инсценировка)
Действующие лица: Магистр рассеянных наук, мальчик и девочка.
Учитель:
Однажды с Магистром рассеянных наук произошел такой случай. Собрался он в путешествие, вышел на улицу и увидел на скамейке двух плачущих детей. Сейчас, ребята, вы просмотрите сценку и постарайтесь найти ошибку в рассуждениях Магистра.
Магистр:
Что случилось? Вы, наверное, потеряли деньги?
Девочка:
Нет. Мне мама велела купить ровно три четверти литра квасу.
Мальчик:
А мне пол-литра, а бутылку я разбил. Куда мне теперь налить квас?
Девочка:
В бидон входит только один литр.
Магистр:
Вам, дети повезло, что вы встретились со мной. А арифметика нам поможет. Тебе, девочка, нужно купить три четверти литра квасу - это ![]() , а тебе, мальчик, пол-литра - это
, а тебе, мальчик, пол-литра - это ![]() .
.
Теперь сложим эти дроби: ![]() , а в бидон входит 1 л, или
, а в бидон входит 1 л, или ![]()
л, так что квасу вы нальете, а бидона останется пустой.
Учитель:
После этих слов дети еще громче заплакали и убежали. Почему?
Объяснение. (найдите ошибку)
-Ребята, мы с вами изучили не все понятия, связанные с дробями. У нас с вами есть «будущее». Сложение дробей с разными знаменателями мы изучим
позже.
Русский математик Магницкий писал в своей знаменитой «Арифметике»:
Не тот арифметик,
Кто в целых ответчик,
А в долях ничтоже
Отвечать возможе.
Сегодня мы поднялись на верхние ступени арифметики.
Пришло время расставания. Мы с вами на этой временной шкале находимся дальше всех тех, о ком мы сегодня говорили.
О, мудрецы времен!
Умней вас не сыскать.
Урок сегодня завершен,
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут!
Результативность. Получение информации об уровне знаний, умений и навыков каждого учащегося. Систематизация знаний по теме (или темам). Вычисление опорных знаний и ведущих понятий темы. Формирование навыков исследовательской работы. Вооружение основными умениями и навыками, необходимыми для владения данной темой по программе. Формирование навыков исследовательской самостоятельной работы.
ЛИТЕРАТУРА
С.И. Демидова, Л.О. Денищева «Самостоятельная деятельность учащихся при обучении математике»-М:,Просвищение-1985г.-192с.
«Математика в школе»№3-1998г.,с.37
«Математика в школе»№2-1999г.,с.53
Газета «Математика»№33-1999г.
Газета «Математика»№16-1998г.
В.В. Вавилов, И.И. Мельников, С.Н. Олехник, П.И. Пасеченко «Задачи по математике. Начало анализа: Справочное пособие» - М:, Наука. Гл. ред. Физ. - мат. лит.,1990-608с.
В.Г. Болтянский, Ю.В. Сидоров, М.И, Шабунин, А.Б. Марткович «Математика. Лекции, задачи, решение» - Минск, Издательство»Альфа»-1994г.-638с.
«Математика в школе» №6 – 1996г. 21с.
«Математика в школе» №5 – 1999г. 2с.
Г.И. Багатырев, О.А. Боковнев, «Математика для подготовительных курсов техникумов»
А.Я. Симонов, Д.С. Бакаев, А.Г. Эпельман «Система тренировочных задач и упражнений по математике» М.:Просвещение,1991г.-208с.
Кордемский Б.А., Ахадов А.А. Удивительный мир чисел. – М., Просвещение, 1986
Лоповок Л.М. 1000 проблемных задач по математике. – М., Просвещение, 1995.
Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. – М., Просвещение, 1984.
Сергеев И.Н., Олехник С.Н. Примени математику. – М. Наука, 1990.
Из опыта работы учителя математики Обуховой Л.Н.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ