Конспект урока по математике "Показательная функция" 11 класс
Тема урока: «Показательная функция»
Класс: 11
Ельцова Наталия Ивановна,
учитель математики
МОУ «Александровская СОШ»
Таловского района Воронежской области
Тип урока: урок изучения нового материала.
Цель урока: рассмотреть показательную функцию, ее свойства и график
Задачи урока:
Образовательные: обеспечить усвоение каждым учащимся знаний о показательной функции, её свойствах, использовании свойств при решении задач
Развивающие: создать условия для развития умений получать знания посредством проведения исследовательской деятельности и анализа ситуации.
Воспитательные: прививать умение сотрудничать
Современные образовательные технологии: развивающее обучение, использование информационно-коммуникативных, здоровьесберегающих технологий.
Методы обучения: словесные, наглядные, практические, методы стимулирования к обучению и побуждение к поиску альтернативных решений.
Формы работы на уроке: фронтальная, групповая, работа в парах, индивидуальная.
Формы контроля: самоконтроль, самооценка, контроль учителя
Средства обучения: ИКТ, программа Excel (электронный тест), классная доска, учебник «Алгебра и начала анализа», тетрадь, чертёжные инструменты.
Ход урока
Орг. Момент
Эпиграфом нашего урока я хочу предложить слова Г. Лессинга «Спорьте, заблуждайтесь, ошибайтесь, но, ради Бога, размышляйте, и, хотя криво – да сами». Вам предстоит сегодня много рассуждать, делать выводы, спорить.
В жизни мы часто сталкиваемся с зависимостями между величин. Оценка по контрольной работе зависит от количества и правильности выполненных заданий, стоимость покупки от количества купленного товара и цен. Одни зависимости носят случайный характер, другие постоянны.
2. Изучение новой темы
а) определение (№ 1)
Давайте рассмотрим следующие законы. (№2)
Р![]() ост древесины происходит по закону:
ост древесины происходит по закону:
A- изменение количества древесины во времени;
A0- начальное количество древесины;
t-время, к, а- некоторые постоянные.
![]()
Давление воздуха убывает с высотой по закону:
P- давление на высоте h,
P0 - давление на уровне моря,
а- некоторая постоянная.
(№3)
-Что общее объединяет эти процессы?( дети отвечают, отмечая схожесть вида формулы, задающей закон)
-Положим в этих формулах с=1,к=1, какую функцию получим?
(у=ах)
Открыли тетради и записали число, тему урока «Показательная функция».(№4)
И сегодня на уроке, мы должны дать определение показательной функции, рассмотреть некоторые свойства и научится применять эти свойства при выполнении заданий, определенного вида. (№ 5)
Начнем с того, что осветим в памяти основные моменты из области функций.
1 Вопрос: Что называется функцией или функциональной зависимостью?
Ответ: Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
Х – независимая переменная – аргумент.
У – зависимая переменная - значение функции.
Итак, попробуйте сформулировать определение показательной функции.
Любое значение основания степени можно брать?
Ответ: Скорее всего нет, так как правая часть -это степень, а степень определена для любого действительного показателя, при а>0.
Вопрос: Итак, решено, а>0. Давайте теперь возьмем а=1. Какой вид примет показательная функция?
Ответ: ( у=1х), но 1 в любой степени это 1, то есть ничего не меняется. Получается линейная функция
Подведем итог: Исключим из показательных функций основания меньше нуля и наложим условие а≠1.
(учащиеся отвечают, учитель, если нужно корректирует определение).(№6) (На слайде появляется определение).
Как вы думаете почему функция называется показательной?
Ответ: Переменная в показателе степени
Запишите определение в тетрадь. (учащиеся записывают его в тетрадь)
б) практическая работа.
Сейчас мы выполним практическую работу.( №8)
В программе Excel нужно построить графики функций у=2х ( одна половина учащихся.), у=(1/2)х (другая половина учащихся) на отрезке [-2;3] с шагом 0,5.
После того, как вы построите график данной функции, по предложенной схеме исследуйте функцию.
Посмотрите на схему исследования.(№9)
1. Область определения функции.
2. Область значений функции.
3. Точки пересечения с осями координат.
4.Промежутки возрастания и убывания.
( учащиеся, работая в парах на компьютерах, составляют таблицу, вводит значения х, строят график функции и исследуют функцию)
в) проверка результатов практической работы.(№10,11)
На экране появляются графики функций, учащиеся называют свойства, которые демонстрируются.
Данные свойства, относятся не только к функции у=2х, но и ко всем показательным функциям, у которых основание а>1. Запишите данные свойства в тетрадь.
Ученики делают записи в тетрадях.
Данные свойства, относятся не только к функции у=1/2х, но и ко всем показательным функциям, у которых основание 0<а<1.
5. Закрепление изученного.(№13) прочитать слайд
Я предлагаю вам выполнить некоторые задания по теме нашего урока.
а) Устно. (учащиеся выбирают верный ответ, обосновывая выбор (№№14-18)
А1. Из предложенного списка функций, выбрать ту функцию,
![]()
![]() которая является показательной:
которая является показательной:
![]()
![]()
А2. Дан график функции. Укажите эту функцию
![]()
![]()

![]()
![]()
А3.
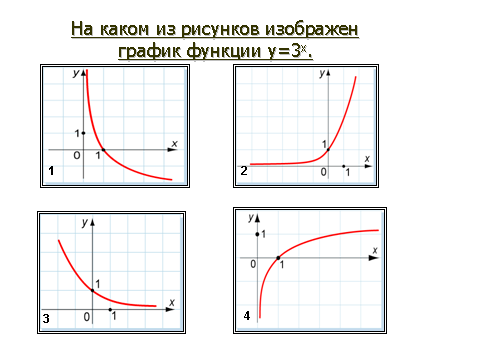
А4. Укажите возрастающую функцию.


![]()
![]()
А5. Укажите убывающую функцию. ![]()
![]()
![]()
![]()
б) Письменно.(№19)
А6. Укажите область значений функции у=4х-1.
Область значений учащиеся находят с помощью преобразований графика
функции (-1;+∞)
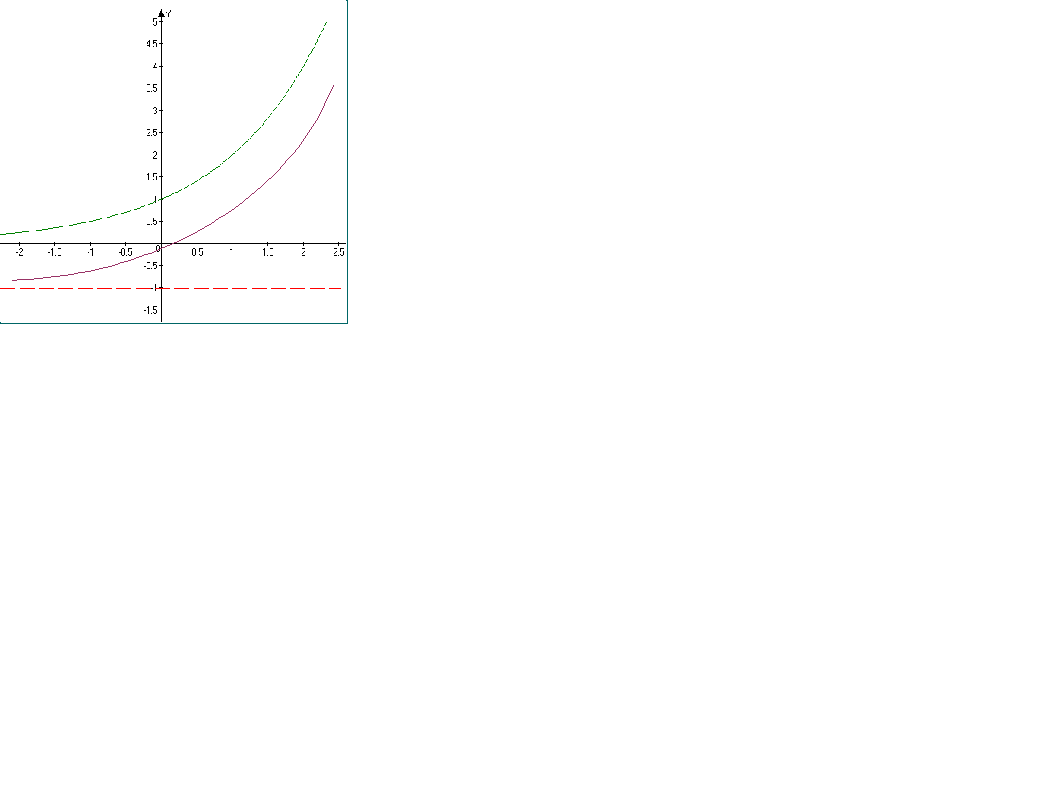
2способ решения
(другой ученик)
у=4х-1.
4х>0 для всех х,
4х-1>0-1
4х-1 = у, значит
у>-1
Е(f) (-1;+∞)
в) формулирование правила. (№№20. 21)
Дана функция: у = ах ± b. Вывести правило, по которому можно,
не выполняя построение графика данной функции,
найти область значения функции.
Вывод:
Если у = а x + b, то Е (у) = (b; +∞)
Если у = а x -b, то Е (у) = (-b; +∞)
г) Самостоятельная работа (с последующей проверкой (№22)
Найти Е(у).
![]()
![]()
![]()
![]()
6. Подведение итогов Выполнение теста на компьютере.
Выставление оценок.
7. Домашнее задание ( на слайде)(№23)

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ