КОНСПЕКТ

УРОКА

«Задачи с параметрами»

Занятие 6

« Системы уравнений

с параметрами»

9 «Д» класс МОУ СОШ № 65

Учитель: Алиско Т. Р.

Элективный курс «Задачи с параметрами»

« Системы уравнений с параметрами»

Цель: образовательные:

- обобщить и систематизировать знания учащихся об исследовании линейных и квадратных уравнений при решении задач с параметрами,

- формирование навыков решения задач с параметрами различными способами.

- формирование умений систематизировать полученные знания и применять их при решении задач с параметрами.

развивающие:

- развитие исследовательской и познавательной деятельности учащихся;

- развитее абстрактного мышления (развитие умений выделять общие и существенные признаки, отличать несущественные признаки и отвлекаться от них)

воспитательные:

- формирование коммуникативных навыков, умение работать в парах и группах.

- обеспечение условий для самостоятельной, творческой работы учащихся, для их самореализации

Ход урока:

I Актуализация знаний

В качестве домашнего задания вам было предложено решить систему уравнений.

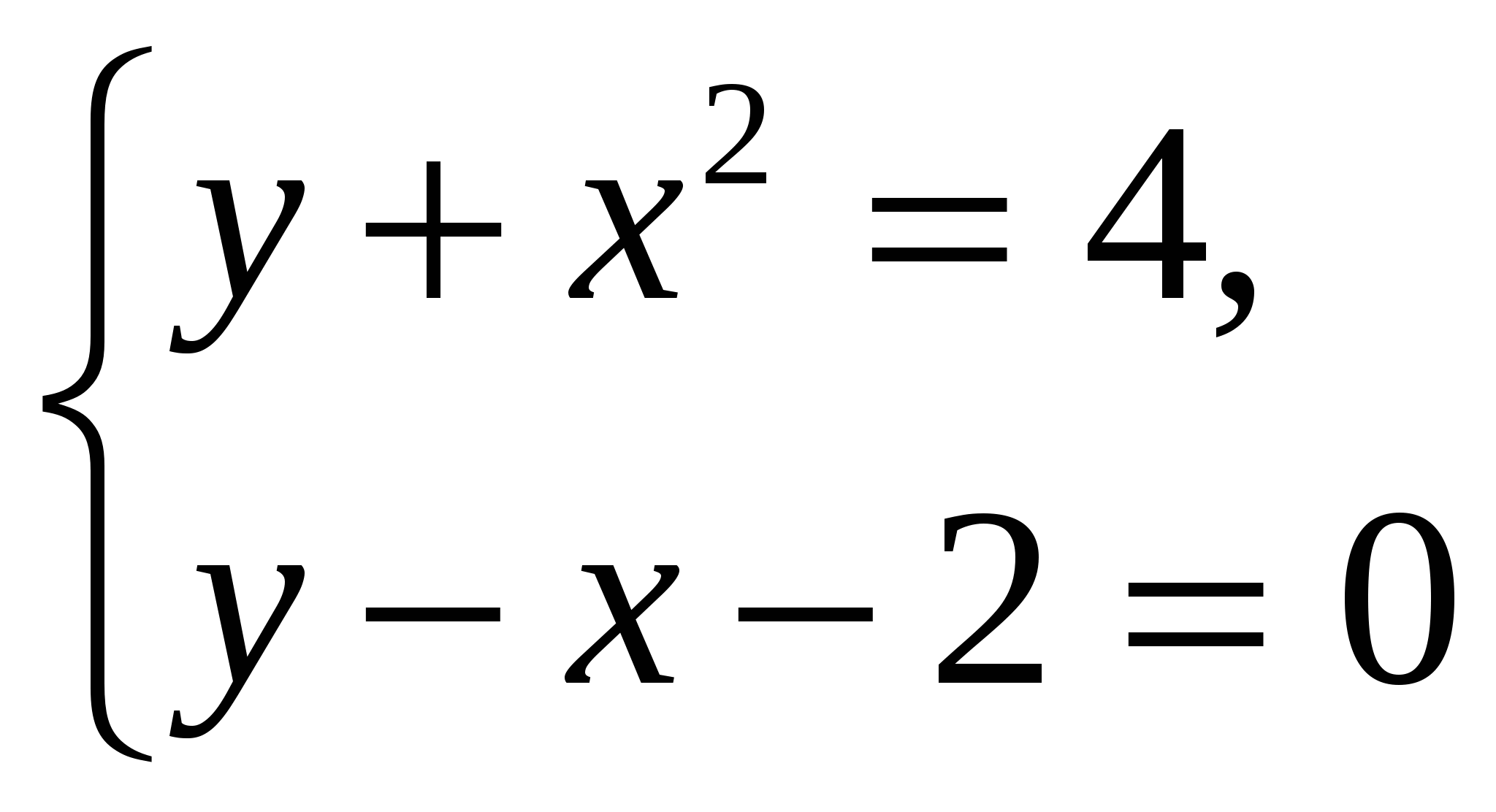
Проверим ваше решение.

С помощью документ – камеры демонстрируется решение системы, разбираются различные методы ее решения.

Наш элективный курс посвящен решению одних из самых сложных задач математики – задачам с параметрами. Необходимость изучения этой темы обусловлена в первую очередь общими подходами к исследованиям тех или иных математических функций, которые в свою очередь, мы с вами часто об этом говорили, являются математической моделью жизненных процессов и явлений.

Мы с вами уже рассмотрели некоторые уравнения с параметрами и особенности их решения. Повторим ранее изученный материал.

Вам предлагается проанализировать решение одного уравнения с параметрами и прокомментировать его.

Слайд № 1.

При каких значениях параметра а уравнение (а+6)х²+2ах+1=0 имеет единственное решение?

Решение:

Уравнение имеет единственное решение, если дискриминант равен нулю.

D=(2а)² - 4(а+6)=4а²-4а-24

4а²-4а-24=0 Разделим обе части уравнения на 4

а²-а-6=0

а = - 2; а = 3

Ответ: при а = - 2; а = 3 уравнение имеет единственное решение.

Повторим схему исследования уравнений с параметрами:

Слайд № 2

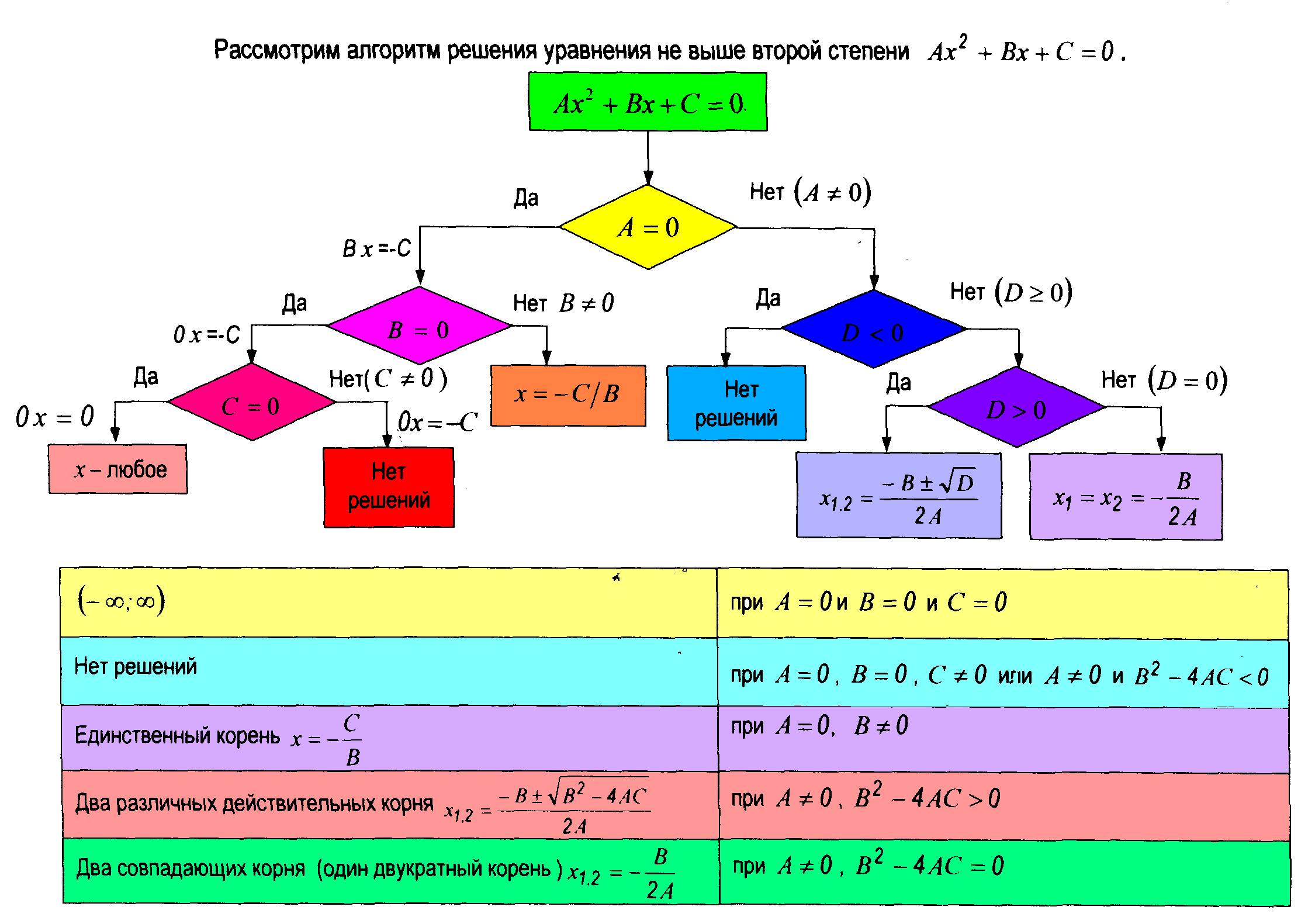
II Изучение нового материала

- Как вы думаете, какие задания мы сегодня с вами усложним за счет параметра?

- Верно, сегодня мы рассмотрим решения систем уравнений с параметрами.

Я вам предлагаю систему двух уравнений с двумя неизвестными.

Слайд № 3

Какие способы ее решения вы можете предложить? Таким образом, цель нашего занятия не просто научиться решать систему уравнений с параметрами , но и рассмотреть различные способы решения: аналитический и графический.

- Кто планирует решать эту систему аналитически? А кто предпочитает графический способ? Объединитесь, пожалуйста в группы по выбранному способу решения.

Ребята меняются местами о объединяются в группы, согласно выбранному способу решения.

- Группа, которая выбрала аналитический метод, запишут свое решение в тетрадях и мы рассмотрим его с помощью документ - камеры. А графический способ мы рассмотрим на интерактивной доске.

Вам дается минут 5-7 на решение.

После проверяются и анализируются решения, предложенные ребятами.

Теперь предлагаю вам еще одну систему уравнений. В чем вы заметили отличие?

- Кто сейчас выбирает группу аналитиков? А кто предпочитает графический способ? Объединитесь, пожалуйста в группы по выбранному способу решения.

- идет, возможно, переформирование групп.

В течении 10 минут ребята обсуждают решение. После чего снова оба решения проверяются.

Итог урока:

Мы сегодня рассмотрели разные методы решения заданий с параметрами. Какой метод вам ближе? Почему?

В качестве домашнего задания я предлагаю вам достаточно сложную систему, аналогичное задание было в этом году на ЕГЭ.

При каких значения параметра система имеет единственное решение

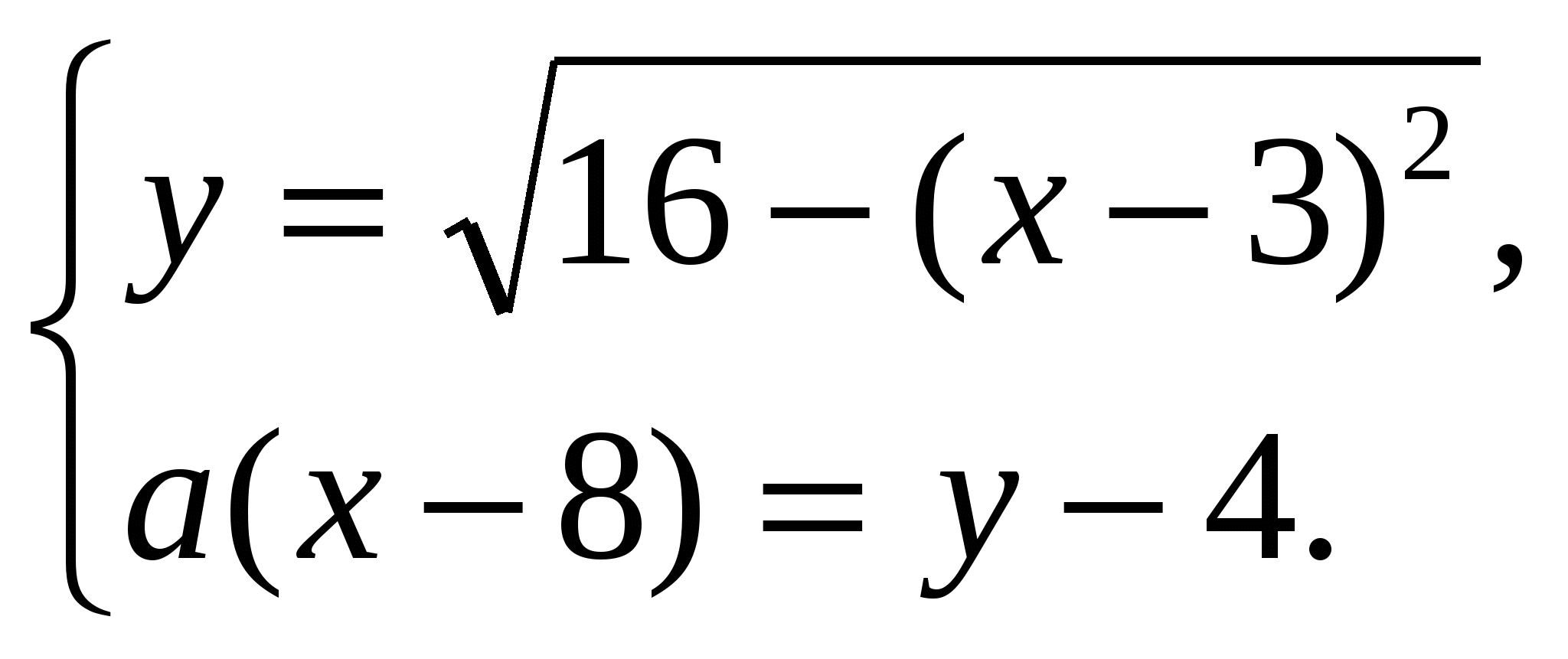
Попробуйте решить ее разными способами.

Рефлексия: