Кружок 5 класса

Принцип Дирихле

1.В магазин привезли 25 ящиков яблок трех сортов. В каждом ящике лежат яблоки одного сорта. Продавец утверждает, что у него нет девяти ящиков с яблоками одного сорта. Не ошибся ли он?

2.В поход пошли 20 туристов. Самому старшему из них 35 лет, а самому младшему а) 16 лет б) 17 лет. Верно ли, что среди туристов есть одногодки?

3.В школе учатся 400 учеников. Докажите, что хотя бы двое из них отмечают день рождения в один и тот же день.

4.Сможете ли вы разложить 44 шарика на 9 кучек так, чтобы количество шариков в разных кучках было различным?

5.Занятия математического кружка проходят в девяти аудиториях. Среди прочих, на эти занятия приходят 19 учеников из одной и той же школы. 
а) Докажите, что как их не пересаживай, хотя бы в одной аудитории окажется не меньше трех таких школьников. 
б) Верно ли, что в какой-нибудь аудитории обязательно окажется ровно три таких школьника?

6.Докажите, что в любой компании из 5 человек есть двое, имеющие одинаковое число знакомых в этой компании.

Дополнительные задачи 1

7.Несколько футбольных команд проводят турнир в один круг. Докажите, что в любой момент турнира найдутся команды, сыгравшие к этому моменту одинаковое количество матчей.

8.Каждая грань куба окрашена в черный или белый цвет. Докажите, что найдутся две грани с общим ребром, которые одинаково окрашены.

9.Какое наибольшее число королей можно поставить на шахматной доске так, чтобы никакие два из них не били друг друга?

10.Докажите, что никакая прямая не может пересекать все три стороны треугольника.

11.По краю круглого стола равномерно расставлены таблички с фамилиями дипломатов, участвующих в переговорах. После начала переговоров оказалось, что ни один из них не сидит напротив своей таблички. Можно ли повернуть стол так, чтобы по крайней мере два дипломата сидели напротив своих табличек?

5 класс

Домашнее задание 1

1.Из трех монет одна фальшивая, она легче остальных. За сколько взвешиваний на чашечных весах без гирь можно определить, какая именно?

Решение. Необходимо провести хотя бы одно взвешивание. Положим по монете на чаши весов. Если весы в равновесии, то фальшивая монета лежит на столе, иначе фальшивая та, которая лежит на весах и легче.

2.Во сколько раз километр больше миллиметра?

Решение. 1 км = 1000 м = 100000 см = 1000000 мм

3.Сумма двух чисел 179. Одно из них больше другого на 61. Найдите эти числа.

Решение. 179-61=118 - удвоенное первое число,

118:2=59 - первое число,

59+61=120 - второе число.

4.Расстояние между двумя машинами, едущими по шоссе, равно 200 км. Скорости машин: 60 км/ч и 80 км/ч. Какое может быть расстояние между ними через 1 час?

Решение. Существует четыре варианта движения машин друг относительно друга.

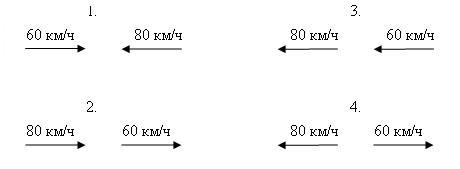
вариант 1: v=80+60=140 км/ч - скорость сближения,

s=200-140=60 км - расстояние между машинами через час.

вариант 2: v=80-60=20 км/ч - скорость сближения машин,

s=200-20=180 км - расстояние между машинами через час.

вариант 3: v=80-60=20 км/ч - скорость удаления машин машин друг от друга,

s=200+20=220 км - расстояние между машинами через час.

вариант 4: v=80+60=140 км/ч - скорость удаления машин друг от друга,

s=200+140=340 км - расстояние между машинами через один час.

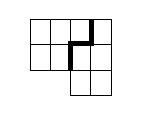
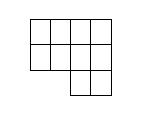
5.Разрезать данную фигуру на две равные части.

Ответ. см. рисунок.

Домашнее задание 1

1.Из трех монет одна фальшивая, она легче остальных. За сколько взвешиваний на чашечных весах без гирь можно определить, какая именно?

2.Во сколько раз километр больше миллиметра?

3.Сумма двух чисел 179. Одно из них больше другого на 61. Найдите эти числа.

4.Расстояние между двумя машинами, едущими по шоссе, равно 200 км. Скорости машин: 60 км/ч и 80 км/ч. Какое может быть расстояние между ними через 1 час?

5.Разрезать данную фигуру на две равные части.

Домашнее задание 1

1.Из трех монет одна фальшивая, она легче остальных. За сколько взвешиваний на чашечных весах без гирь можно определить, какая именно?

2.Во сколько раз километр больше миллиметра?

3.Сумма двух чисел 179. Одно из них больше другого на 61. Найдите эти числа.

4.Расстояние между двумя машинами, едущими по шоссе, равно 200 км. Скорости машин: 60 км/ч и 80 км/ч. Какое может быть расстояние между ними через 1 час?

5.Разрезать данную фигуру на две равные части.

Домашнее задание 1

1.Из трех монет одна фальшивая, она легче остальных. За сколько взвешиваний на чашечных весах без гирь можно определить, какая именно?

2.Во сколько раз километр больше миллиметра?

3.Сумма двух чисел 179. Одно из них больше другого на 61. Найдите эти числа.

4.Расстояние между двумя машинами, едущими по шоссе, равно 200 км. Скорости машин: 60 км/ч и 80 км/ч. Какое может быть расстояние между ними через 1 час?

5.Разрезать данную фигуру на две равные части.

Олимпиадные задачи по математике на принцип Дирихле

1) Родители 25 учеников 5 класса «А» купили своим детям мобильные телефоны восьми разных моделей. Найдутся ли четыре ученика, имеющие телефоны одной модели?

2) В спортивный лагерь приехали отдыхать 97 человек. Докажите, что среди них найдутся хотя бы 9 человек, родившихся в один месяц.

3) В кондитерский отдел завезли 45 коробок с конфетами пяти разных наименований, причем в каждой коробке лежат конфеты только какого-то одного наименования. Найдутся ли 9 коробок с конфетами одного наименования?

4) Вычислите значение дроби:
В ней разные буквы (множители) заменяют разные цифры, между которыми стоит знак умножения)

5) Лена и Борис играют в интересную игру. Лена рассыпает на шахматной доске 195 маленьких бусинок, а Борис пытается найти 4 бусинки, попавшие в одно поле. Если ему это удается, то он выигрывает. В противном случае выигрывает Лена. Кто из них обязательно выиграет, а кто проиграет?

6) Учитель математики объявил результаты самостоятельной работы, проведенной в 5 классе. Наибольшее число ошибок имел Олег. У него было ровно 13 ошибок. Можно ли найти среди 28 учащихся 5 класса, допустивших ошибки, три ученика с одинаковым количеством ошибок?

7) Какое максимальное количество клеток на доске размером 6×6 можно закрасить, чтобы никакие две из закрашенных клеток не соприкасались (даже в одной точке).

Историческая справка репетитора математики:
Петер Густав Лежен Дирихле (1805—1859) — великий немецкий математик, оставивший после себя несколько важных открытий в различных областях математики и физики: в математическом анализе (признак Дирихле сходимости ряда, функция Дирихле), в теории чисел (теорема Дирихле о простых числах в арифметической прогрессии). Имеются труды по математической физике (принцип Дирихле в теории гармонических функций).

Формулировка принципа Дирихле: При раскладывании (распределении) k предметов по n ящикам (классам) обязательно найдется ящик (класс), в котором количество этих предметов не меньше чем .

Знакомство с принципом Дирихле.

Задача 1.

В городе Формалюнске 15 школ. В них обучается 6015 школьников. В концертном зале городского Дворца Культуры 400 мест. Доказать, что найдется школа, ученики которой не поместятся в этот зал.

Решение задачи №1.

Предположим, что в каждой школе не более 400 учеников. Значит, в 15 школах не более 15 •400=6 000 школьников. Но по условию в школах обучается 6015 человек. Значит, найдется школа, в которой больше 400 учеников. Поэтому ученики этой школы не поместятся в зал на 400 мест.

Задача 2.

В школьном совете 17 парламентеров. За время заседаний часть из них поссорились между собой. Доказать, что найдутся два участника совета, которые поссорились с одинаковым количеством парламентеров.

Решение задачи №2.

Предположим, что все парламентеры поссорились с различным количеством своих коллег. Посчитаем, сколько может быть различных вариантов. Можно не поссориться ни с кем, поссориться с одним человеком, с двумя, с тремя и так далее до 16 (если поссорился со всеми). Всего получается 17 вариантов поссориться, но если кто-то поссорился со всеми, то не может одновременно быть парламентера, который ни с кем не поссорился. Значит, остается 16 различных вариантов для 17 человек, и найдутся два участника совета, которые поссорились с одинаковым количеством парламентеров.

Задача 3.

В школе 5 восьмых классов: 8"А", ..., 8"Д". В каждом из них учится по 32 человека. Докажите, что найдутся 14 человек, родившихся в один месяц.

Решение задачи №3.

Предположим, что в каждом месяце родилось не более 13 учеников (год рождения не учитывается). Значит, за 12 месяцев родилось не более 12 •13=156 школьников. Но по условию в пяти классах этой школы обучается 5*32=160 человек. Получили противоречие. Значит, найдется месяц, в котором родилось больше 13 учеников, то есть хотя бы 14.

Задача 4.

В 3"А" классе учится 27 школьников, знающих (всего) 109 стихотворений. Докажите, что найдется школьник, знающий не менее пяти стихотворений.

Решение задачи №4.

Предположим, что каждый школьник знает не более 4 стихотворений. Значит, 27 школьников знают не более 4 •27=108 стихотворений. Но по условию они знают 109 стихотворений. Получили противоречие. Значит, найдется школьник, который знает хотя бы 5 стихотворений.

Задача 5.

В походе участвовало 25 человек, каждому из которых было от 24 до 30 полных лет (на данный день). Докажите, что найдутся четыре человека, родившихся в один год.

Решение задачи №5.

Различных годов рождения может быть 7. Предположим, что каждый год родилось не более трех участников похода. Значит, за 7 лет могли родиться не более 3• 7=21 участников. Но, по условию, в походе участвовало 25 человек. Получили противоречие. Значит, найдутся четыре участника похода, родившихся в один год.

Задача 6.

По дороге в школу третьеклассник Коля преодолел 27 луж. Дорога в школу заняла у него 15 минут. Докажите, что найдутся две лужи с паузой менее чем в 35 секунд.

Решение

Если бы между всеми лужами были паузы не менее чем в 35 секунд, то Коля затратил бы на них не менее 35*26=910 секунд, это больше чем 15 минут, что противоречит условию. (26 промежутков, если первая и последние лужи находятся на концах пути.)

Задача 7.

На окно кабинета математики размером 40 см на 30 см село 25 мух. Доказать, что квадратной мухобойкой 11*11 см можно прихлопнуть сразу трех мух.

Решение задачи №7.

Разделим окно на 12 квадратов размером 10 см на 10 см. Если в каждом квадрате не более двух мух, то всего на окне не более 2 •12=24 мух, а по условию мух 25, значит в каком-то квадрате сидит хотя бы 3 мухи. Мухобойка закроет этот квадрат. Значит, такой мухобойкой можно прихлопнуть сразу трех мух.

Знакомство с принципом Дирихле.

1.В городе Формалюнске 15 школ. В них обучается 6015 школьников. В концертном зале городского Дворца Культуры 400 мест. Доказать, что найдется школа, ученики которой не поместятся в этот зал.

2. В школьном совете 17 парламентеров. За время заседаний часть из них поссорились между собой. Доказать, что найдутся два участника совета, которые поссорились с одинаковым количеством парламентеров.

3.В школе 5 восьмых классов: 8"А", ..., 8"Д". В каждом из них учится по 32 человека. Докажите, что найдутся 14 человек, родившихся в один месяц.

4. В 3"А" классе учится 27 школьников, знающих (всего) 109 стихотворений. Докажите, что найдется школьник, знающий не менее пяти стихотворений.

5. В походе участвовало 25 человек, каждому из которых было от 24 до 30 полных лет (на данный день). Докажите, что найдутся четыре человека, родившихся в один год.

6. По дороге в школу третьеклассник Коля преодолел 27 луж. Дорога в школу заняла у него 15 минут. Докажите, что найдутся две лужи с паузой менее чем в 35 секунд.

7. На окно кабинета математики размером 40 см на 30 см село 25 мух. Доказать, что квадратной мухобойкой 11*11 см можно прихлопнуть сразу трех мух.