Методические рекомендации к внеурочной самостоятельной работе "Решение систем уравнений методом Гаусса"
Самостоятельная работа №2
Решение систем уравнений методом Гаусса
Цель работы: овладеть методом Гаусса при решении систем линейных уравнений
Студент должен:
Знать:
символику и формы записи систем линейных уравнений
что такое совместная и несовместная система уравнений
методы решения СЛАУ(метод Гаусса)
Уметь:
применять метод Гаусса
КОНТРОЛЬНЫЕ ВОПРОСЫ:
В каком случае система имеет единственное решение?
В каком случае система имеет бесконечное множество решений?
В чем достоинство метода Гаусса по сравнению с другими методами?
Форма выполнения задания: решение задач (письменно)
Время выполнения 45 мин
Основной теоретический материал
Метод Гаусса. Этот способ заключается в обнулении элементов основной расширенной матрицы системы уравнений, находящихся под главной диагональю.
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы
Алгоритм метода Гаусса
На основании системы линейных уравнений составляем расширенную матрицу системы;
Приводим матрицу к "треугольному" виду;
Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через переменные которые могут принимать произвольные значения;
Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:
Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.
Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.
На первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных, и с помощью несложных математических преобразований она приводится к виду, когда диагональ, состоящая из единичек отсекает нули:
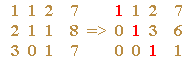
На втором этапе последовательно находятся все неизвестные, начиная с предпоследней.
Решение типовых заданий
Решить систему трех линейных уравнений методом Гаусса
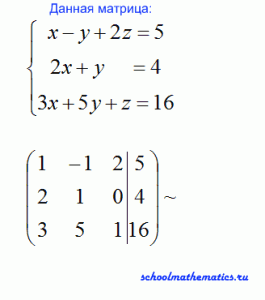
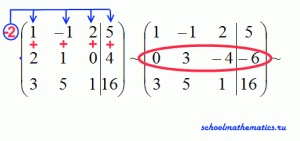
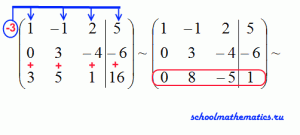
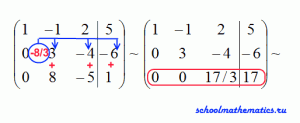
Ответ: х=1, y=2, z=3.
Покажем, как методом Гаусса можно решить следующую систему:
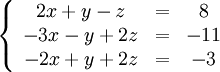
Обнулим коэффициенты при ![]() во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на
во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на ![]() и
и ![]() , соответственно:
, соответственно:
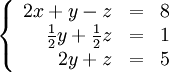
Теперь обнулим коэффициент при ![]() в третьей строке, вычтя из неё вторую строку, умноженную на
в третьей строке, вычтя из неё вторую строку, умноженную на ![]() :
:
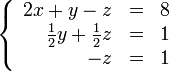
В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
![]() из третьего;
из третьего;
![]() из второго, подставив полученное
из второго, подставив полученное ![]()
![]() из первого, подставив полученные
из первого, подставив полученные ![]() и
и ![]() .
.
Ответ: (2; 3; -1).
Решить самостоятельно системы линейных уравнений по вариантам: 10 вариантов
1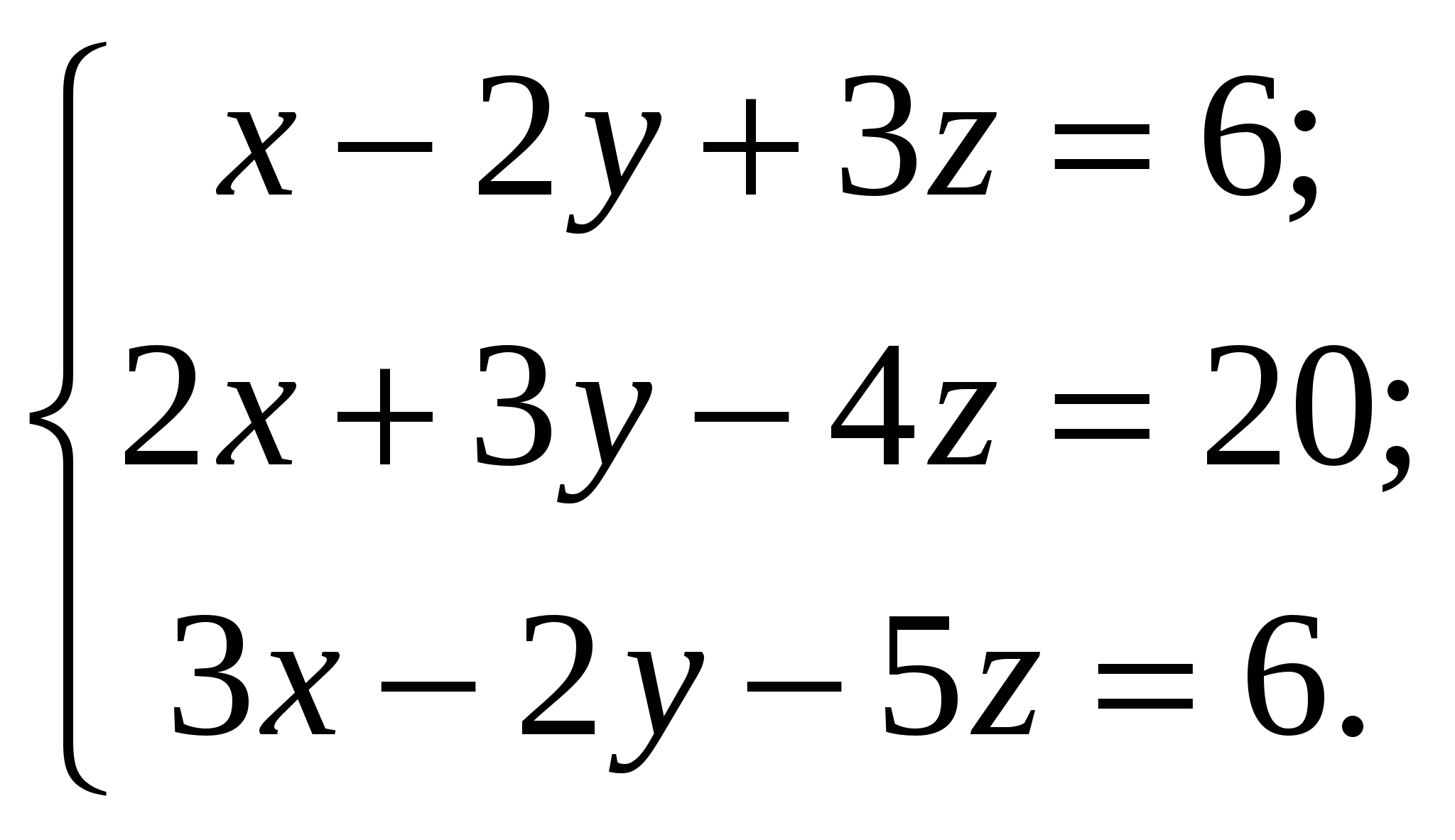
2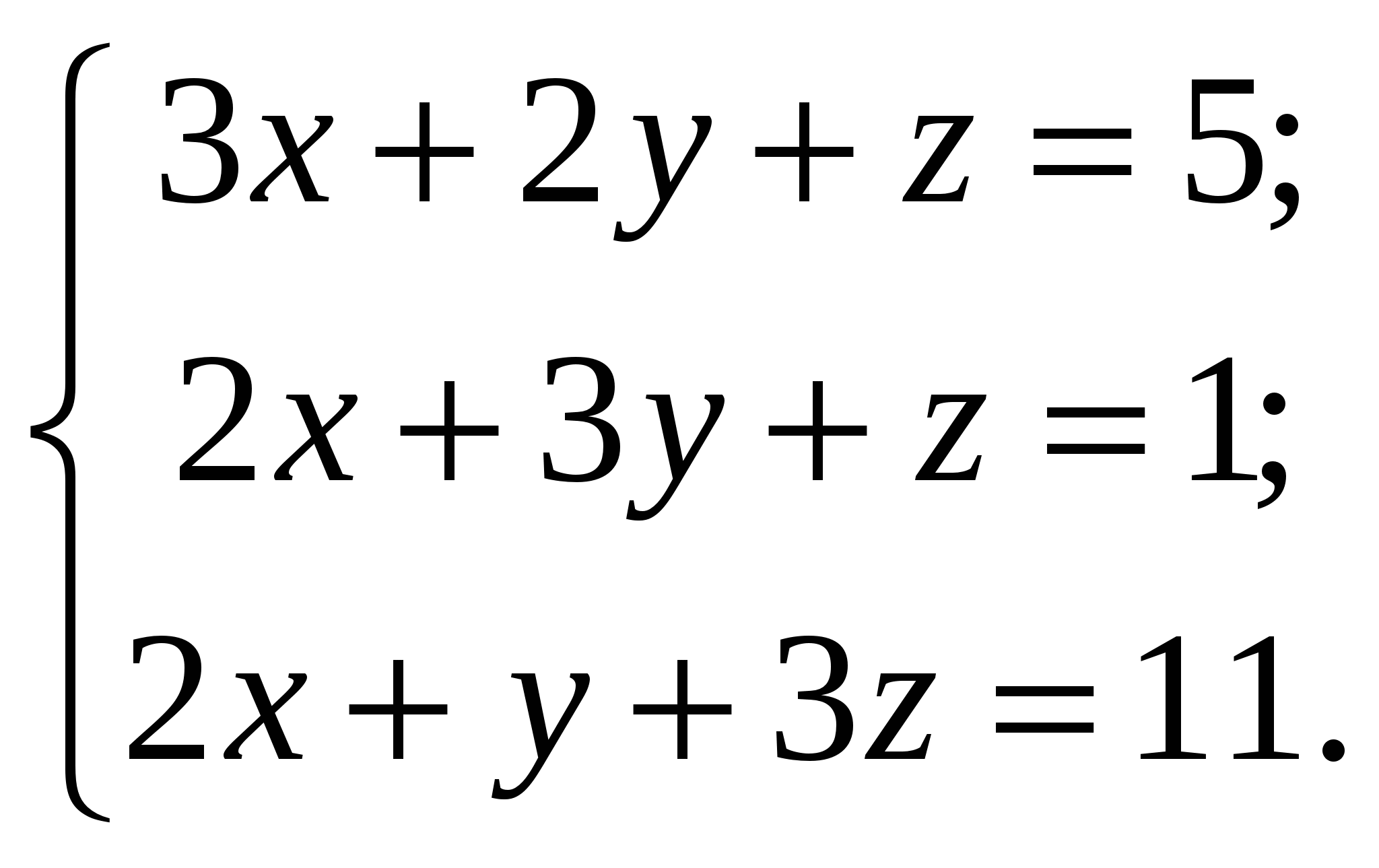
3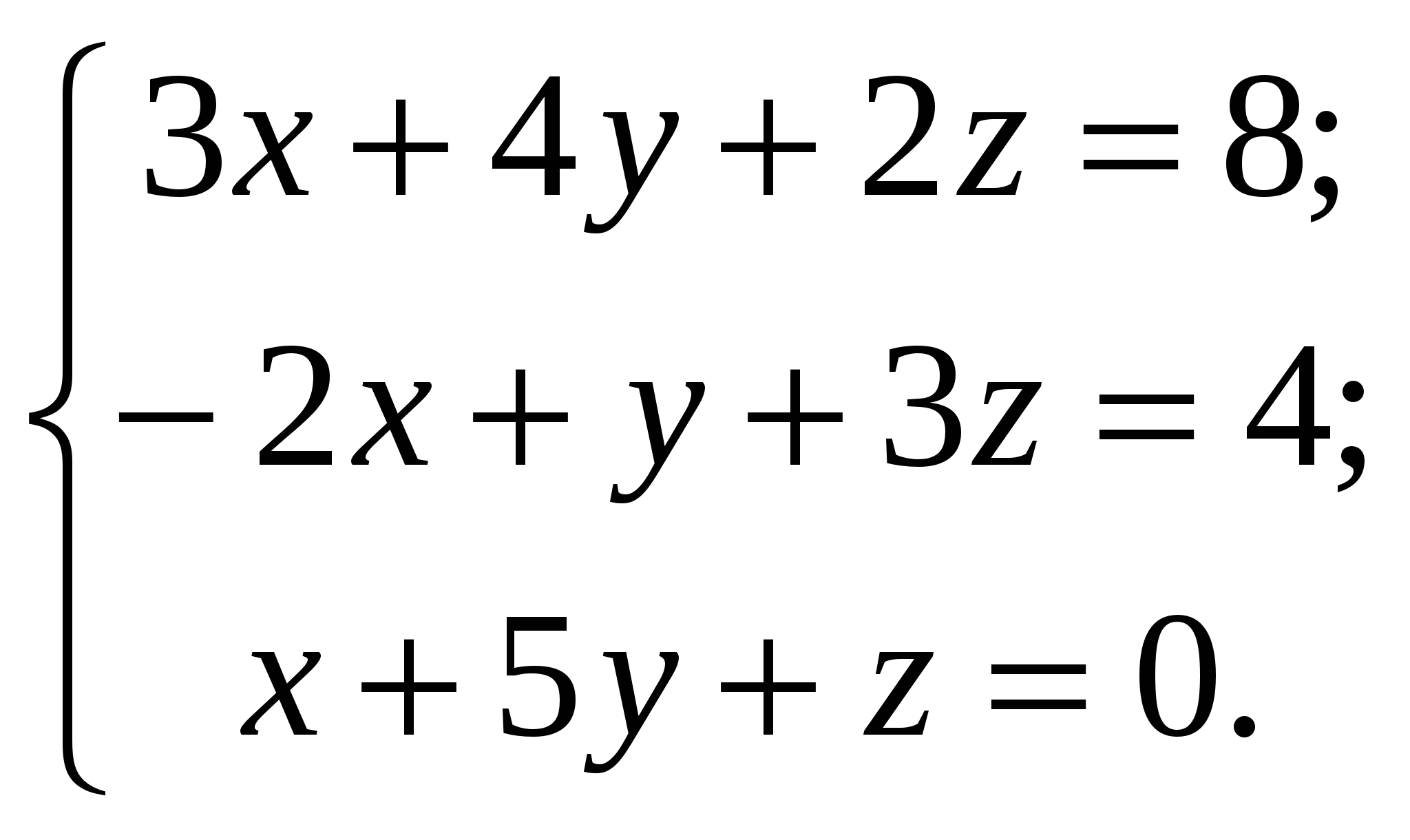
4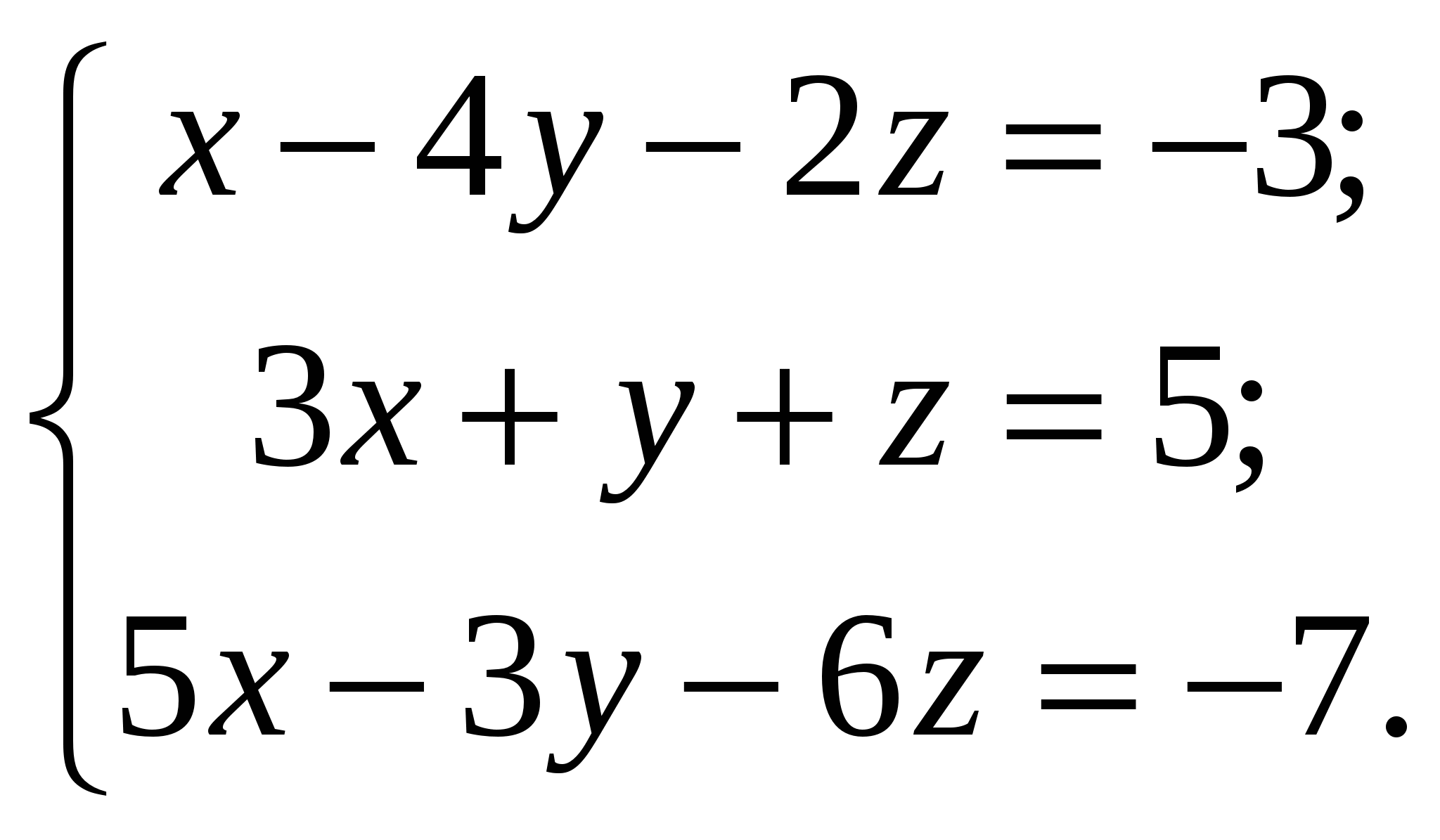
5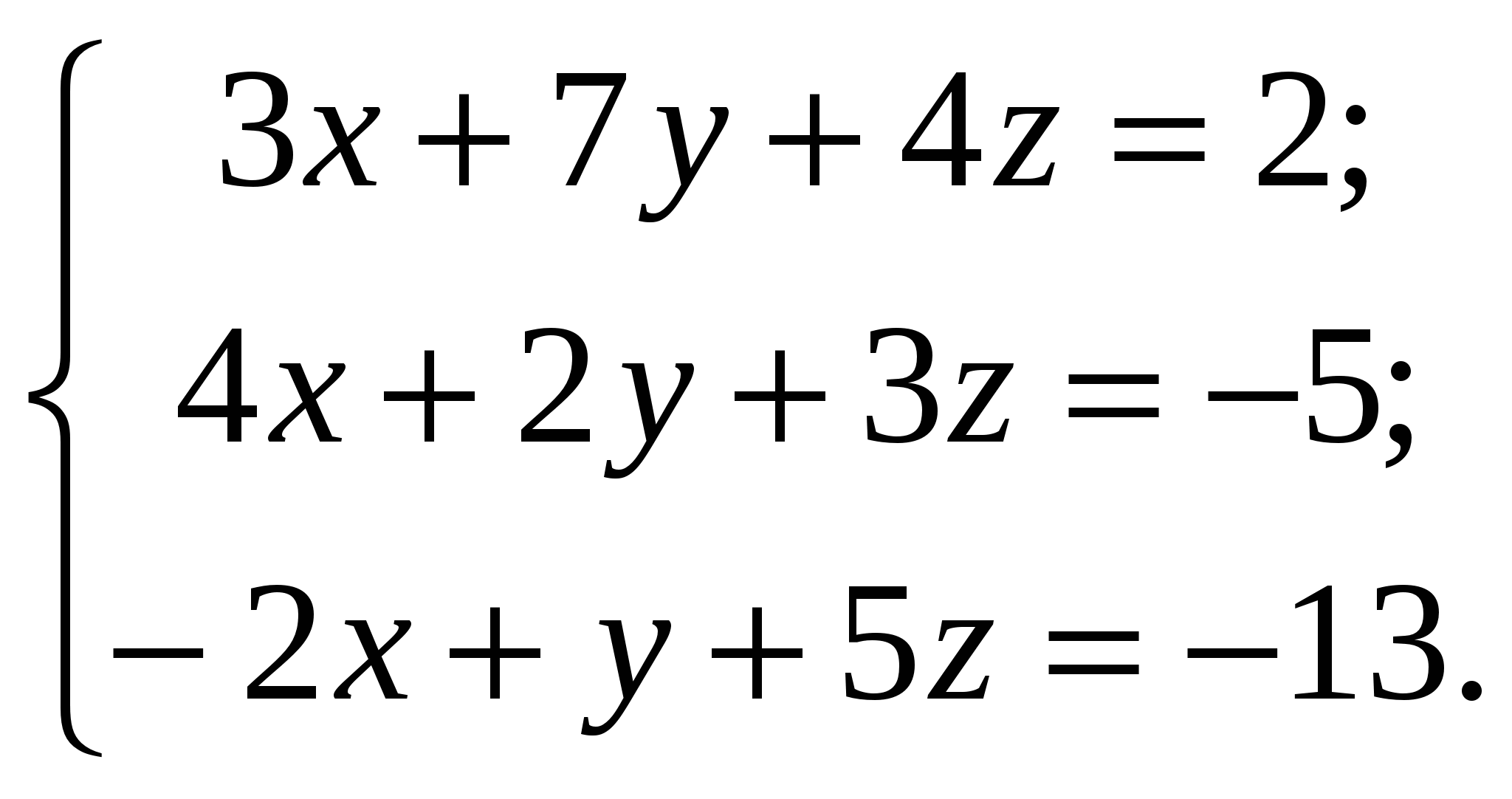
6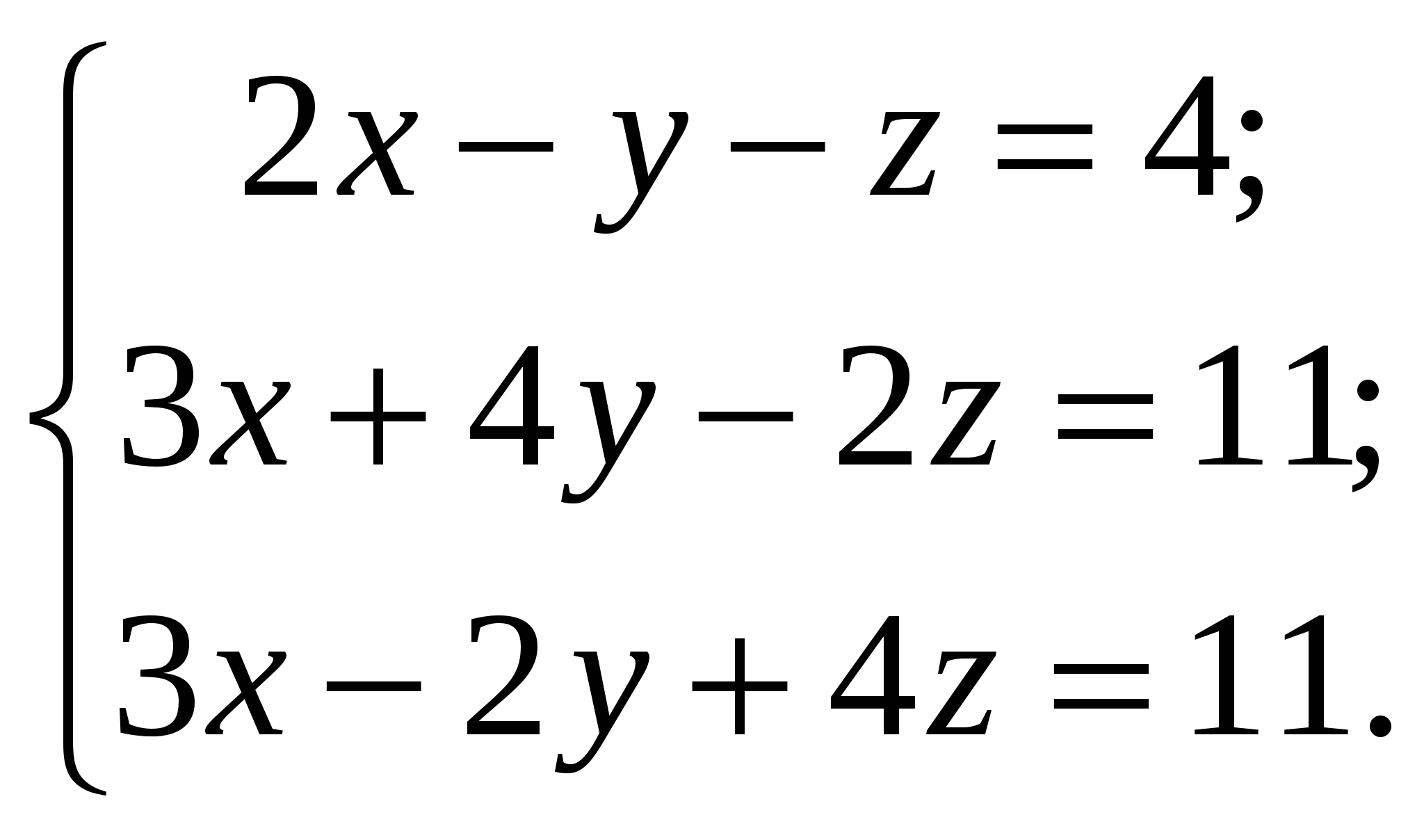
7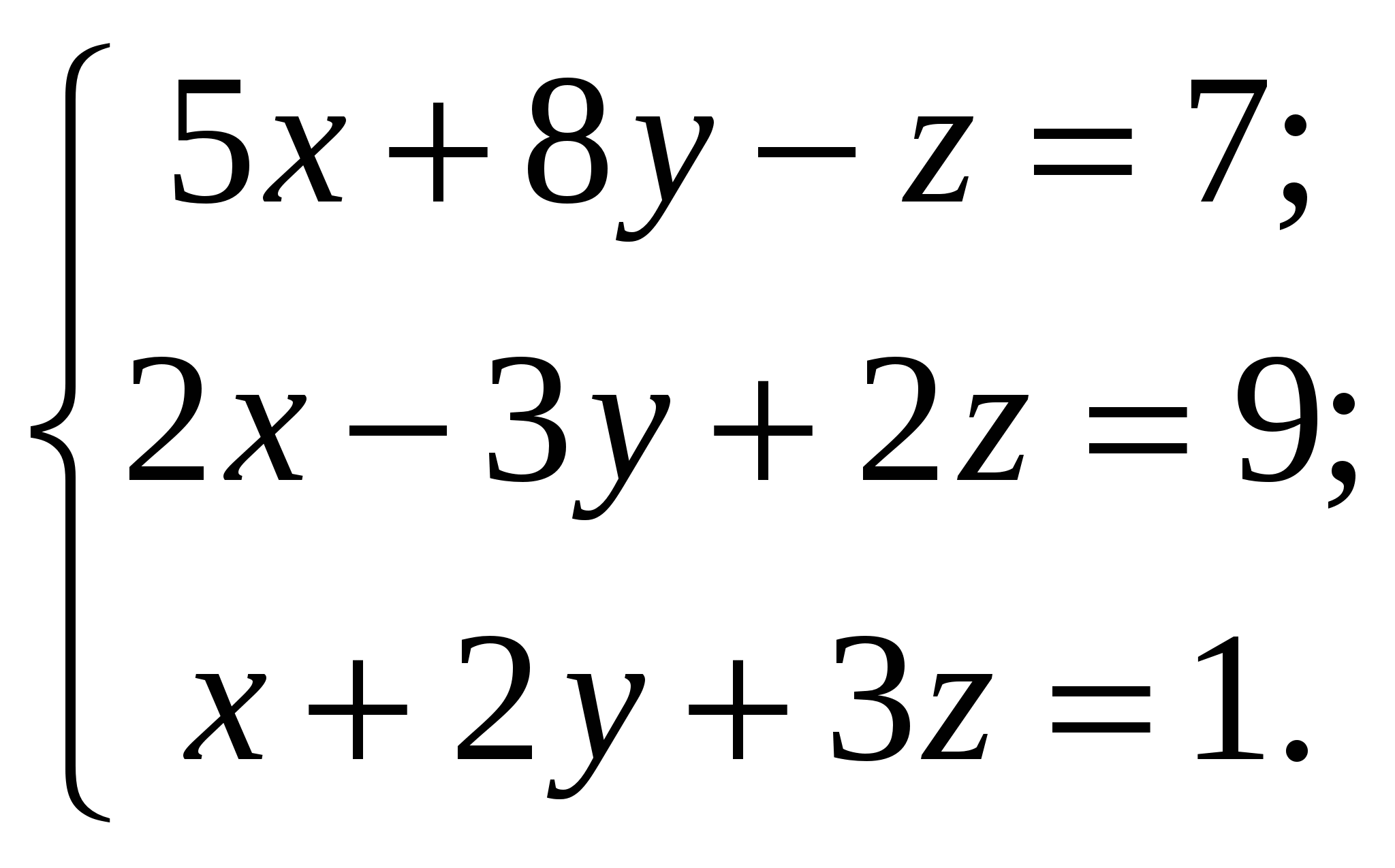
8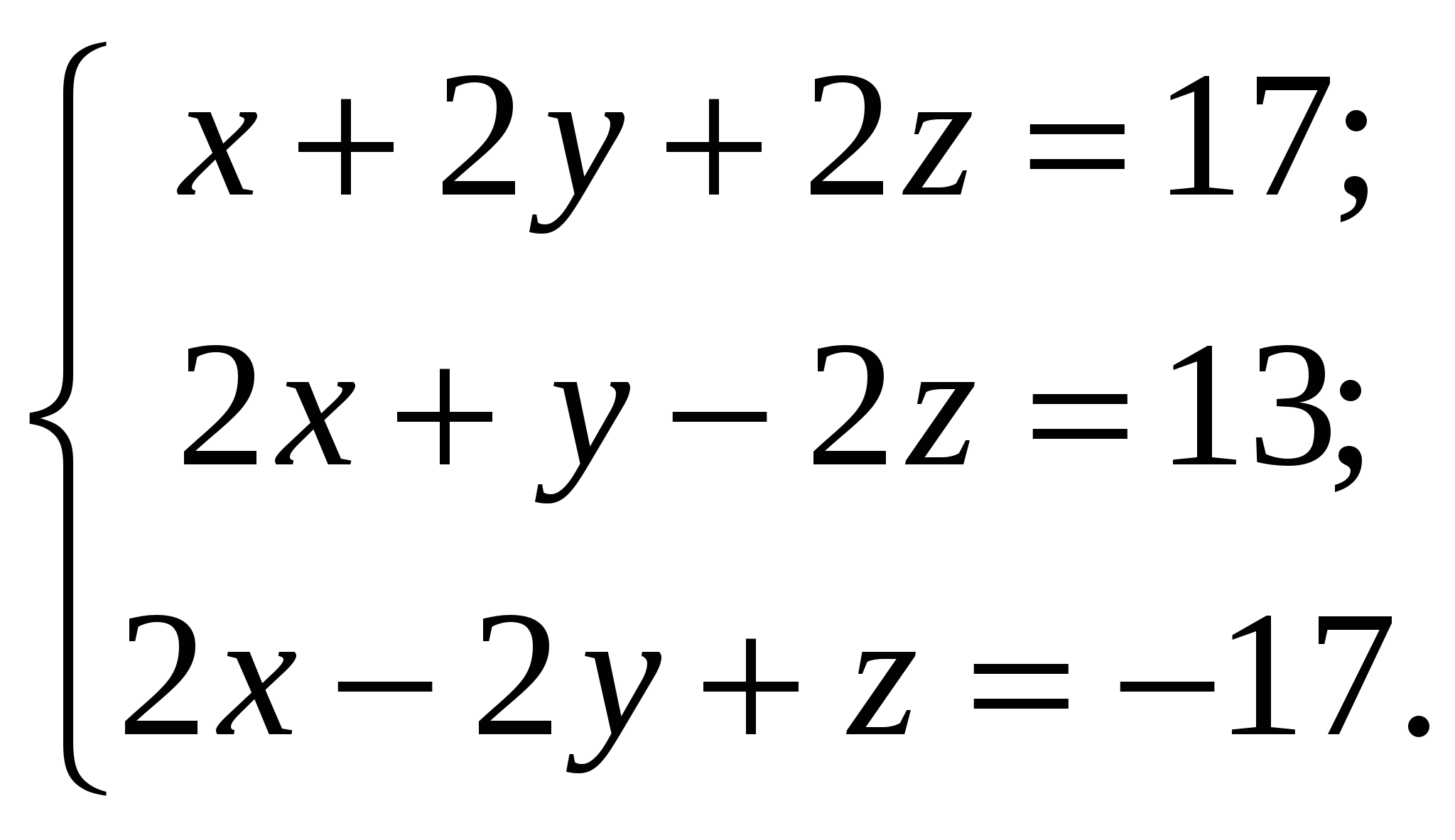
9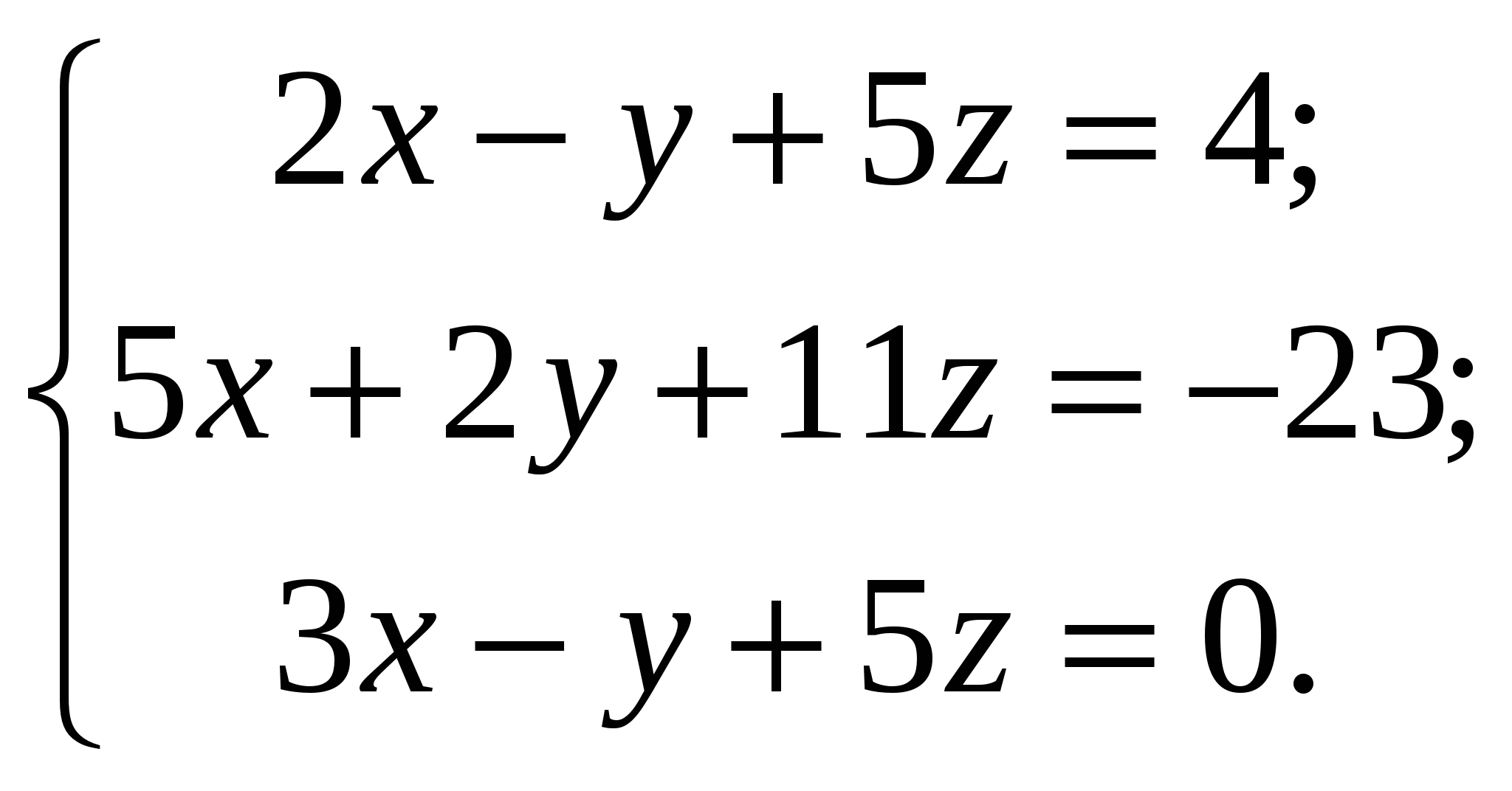
10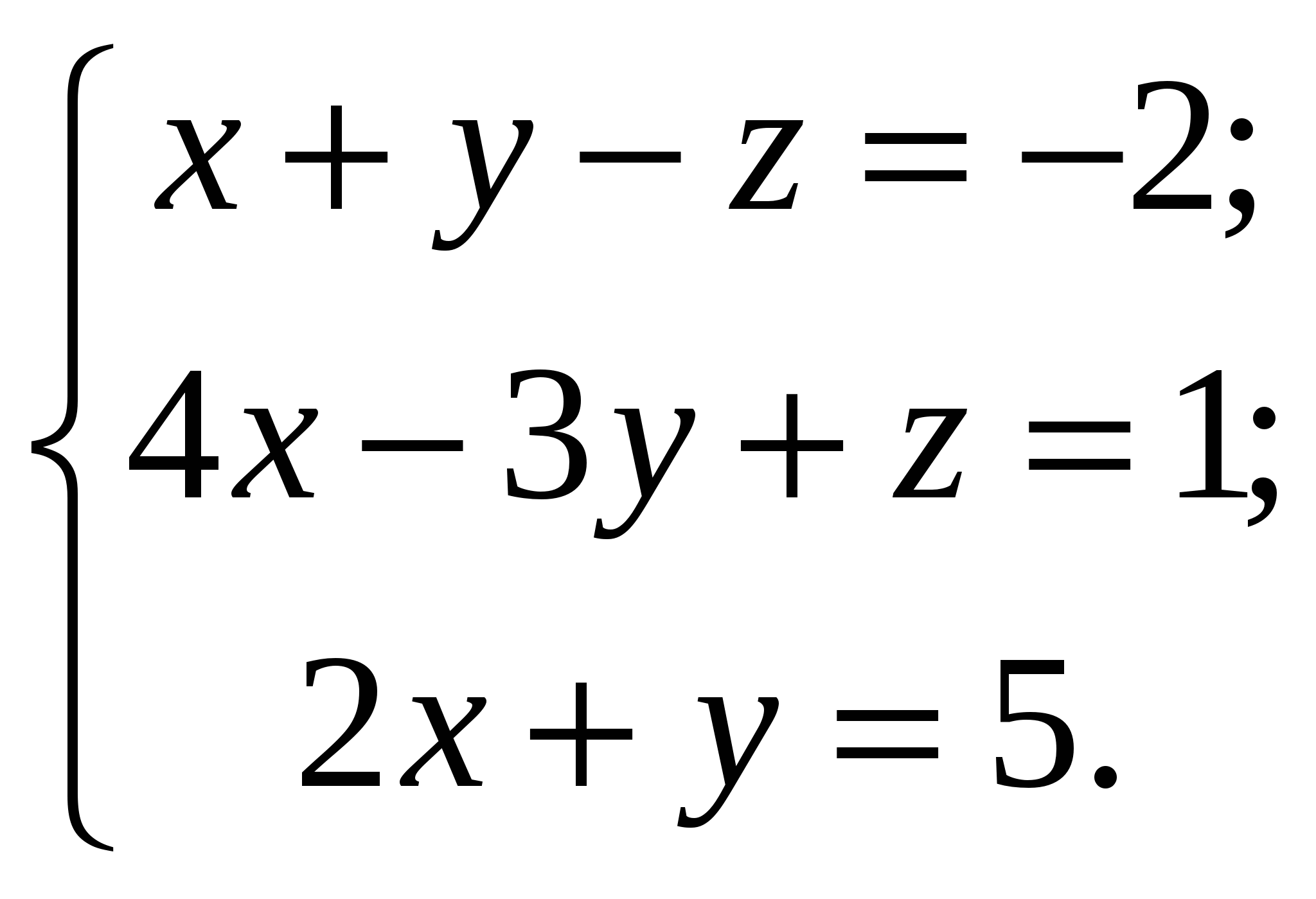
Оформить отчет
Требования к оформлению самостоятельной работы
Расчетные задания должны быть выполнены в рабочей тетради
По результатам решения тренажера выставляется оценка, которая учитывается при приеме дифференцированного зачета.
Шкала оценки образовательных достижений
Процент результативности
(правильных ответов)
Оценка уровня подготовки
Балл (оценка)
Вербальный аналог
90-100
5
отлично
80-89
4
хорошо
70-79
3
удовлетворительно
менее 70
2
неудовлетворительно
Интернет ресурсы
http://math1.ru/education/sys_lin_eq/gauss.html
http://www.bestreferat.ru/referat-180751.html

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ