Олимпиадные задания по математике

для учащихся 8-ых классов

Куст Анжела Эдвардовна

учитель математики

МБОУ гимназии г. Гурьевска

Гурьевского района Калининградской области

Олимпиада по математике

8 класс

1. Запишите число 2000, используя восемь троек, скобки и арифметические операции. (7 баллов)

2. Каково наименьшее натуральное число 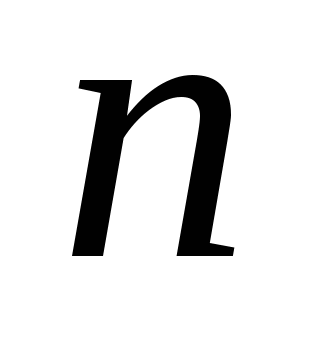, такое, что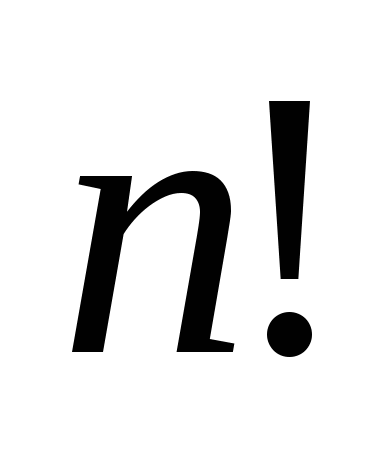

(где ) делится одновременно на 18, 19, 20 и 21? (7 баллов)

3. Трёхзначное число 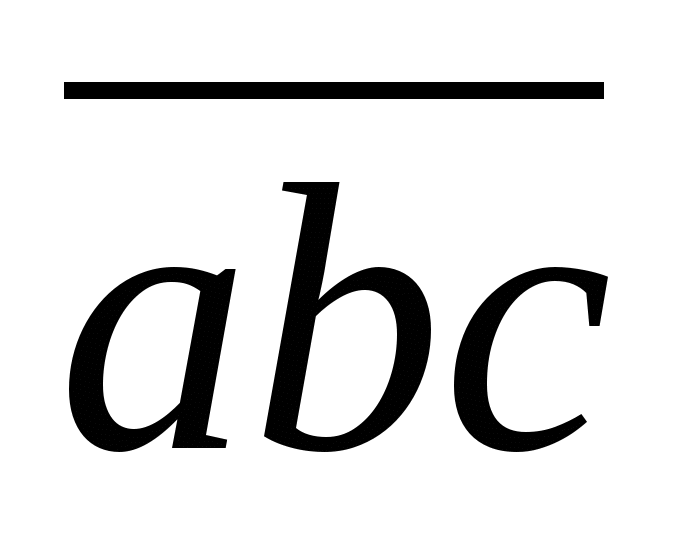делится на 37. Докажите, что сумма чисел

и также делится на 37. (7 баллов)

4. Какое наименьшее количество чисел нужно исключить из набора

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 так, чтобы оставшиеся числа можно было

разбить на две группы с одинаковым произведением чисел в группах?

Приведите пример такого разбиения на группы. (7 баллов)

5. На вопрос о возрасте его детей математик ответил: «У нас трое детей. Когда родился наш первенец, суммарный возраст членов семьи был равен 45 годам, год назад, когда родился третий ребёнок, – 70 лет, а в этом году суммарный возраст детей – 14 лет». Каков возраст детей математика? (7 баллов)

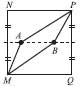
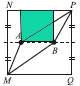
6. MNPQ – квадрат со стороной 6 см, А и В – две точки на его средней линии (средняя линия квадрата – отрезок, соединяющий середины двух его противоположных сторон). Ломанные МАР и МВР делят квадрат на 3 части одинаковой площади. Чему равна длина АВ? (7 баллов)

Ответы и решения

к олимпиадным задачам

1. Например: .

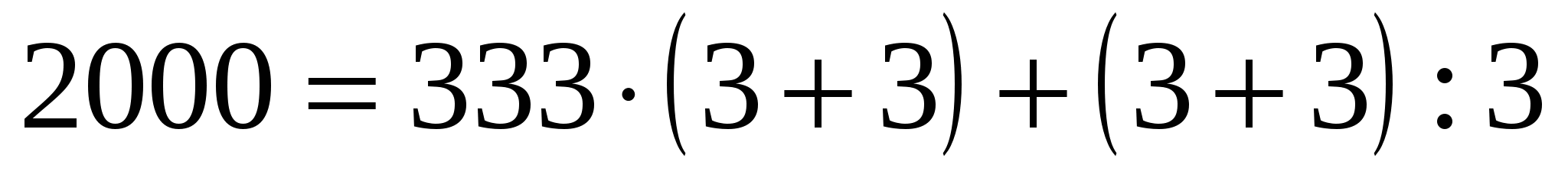2. Ответ: .

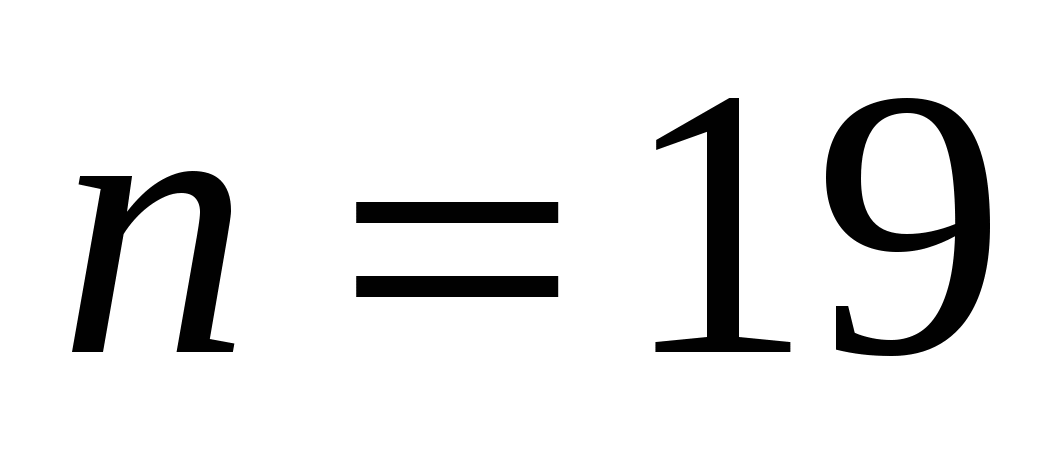3. Ответ:

составим сумму:

По условию число делится на 37, поэтому и сумма

делится на 37.

4. Ответ: нужно исключить три числа, например 3, 7 и 11. Подойдут

группы, произведение чисел в которых равно 1440, например {4, 5, 8, 9}

и {2, 6, 10, 12}. Очевидно, что числа 7 и 11 должны быть исключены.

Произведение остальных чисел есть , поэтому ещё необходимо

исключить число 3 или 12 (так как в произведение число 3 входит в

нечётной степени).

5. Ответ: 1, 5 и 8 лет.
Если первенец старше второго ребёнка на x лет, а средний старше

третьего ребёнка на y лет, то 70 – 45=3(x + y) + y, так как возраст

каждого из родителей и старшего ребёнка к моменту рождения третьего

ребёнка увеличился на (x + y) лет, а возраст второго – на y лет.

Аналогично (x + y + 1) + (y + 1) + 1 = 14. Мы получили систему

уравнений 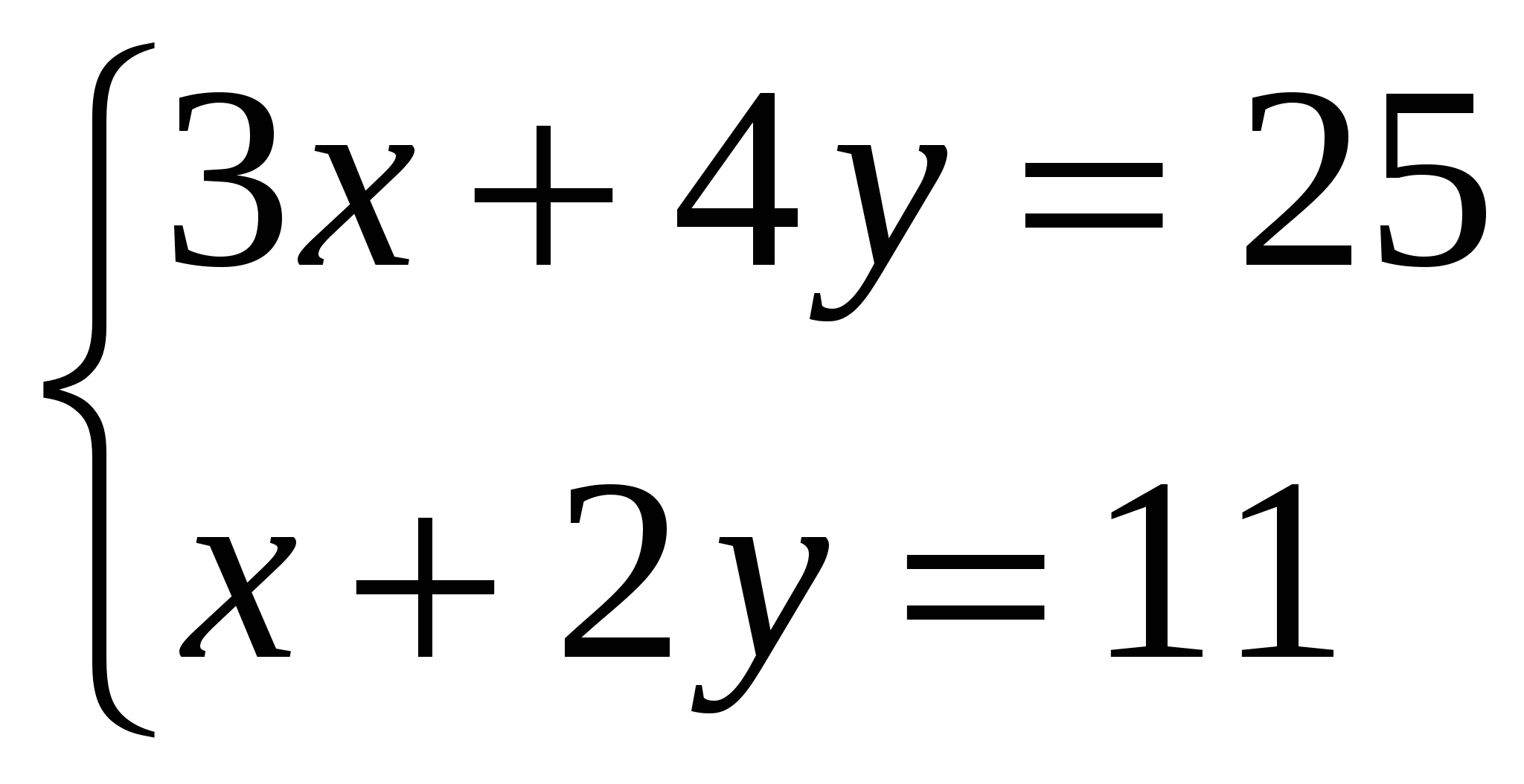, из которой x = 3, y = 4.

6. Ответ: 4 см.
   Восстановим перпендикуляры из точек А и В. Рассмотрим образовавшийся зеленый прямоугольник.

Видно, что его площадь равна площади MBPA и следовательно, равна одной трети площади большого квадрата и равна (6 · 6) : 3 = 12 кв.см.

Высота зеленого прямоугольника равна 6 : 2 = 3 (см). Длина его второй

стороны АВ равна 12 кв.см : 3 см = 4 см.

Список использованной литературы

1. Агаханов Н.Х., Терешин Д.А., Кузнецова Г.М. Школьные математические

олимпиады. – М.: Дрофа, 1999.

2. Горбачёв Н.В. Сборник олимпиадных задач по математике. – М.: МЦНМО,

2004.

3. Агаханов Н.Х., Подлипский О.К. Математика. Районные олимпиады.

6 – 11 классы. – М.: Просвещение, 2010