Опорные задачи

Опорные задачи.

Школьный курс по геометрии это не только теория, но и умение решать задачи. Умение их решать состоит из знаний теории, фактов работающих на умение решать геометрические задачи, методы решения этих задач. Известно, что задача моет служить не только целью, но и средством обучения. Учиться решать задачи с помощью опорных (ключевых, базисных) – древняя идея. Опорные задачи это множество задач специфические методы решения, которых можно использовать при решении целого класса похожих задач.

Можно выделить два типа опорных задач.

1. Задача «факт» – задача, в которой формулируется некий факт, который часто встречается в других задачах. В качестве примера задачи факта можно привести любую теорему.

Медиана, проведенная к гипотенузе

1) В прямоугольном треугольнике длина медианы, выходящей из вершины прямого угла, равна половине длины гипотенузы.

Следствие. Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

2) Если в треугольнике длина медианы равна половине длины основания, к которому она проведена, то этот треугольник прямоугольный.

Расстояние от вершины треугольника до точки касания вписанной окружности со стороной.

П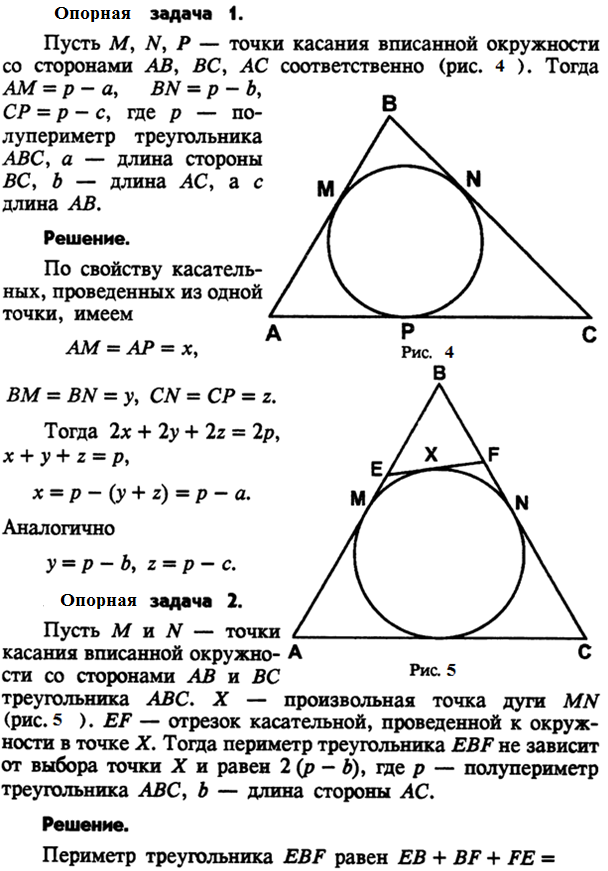усть M, N, P -точки касания вписанной окружности со сторонами AB, BC, AC соответственно. Тогда AM=p-a, BN=p-b, CP=p-c, где p-полупериметр треугольника ABC, a- длина стороны BC, b-длина AC, а с-длина AB.

2. Задача «метод» – это задача, метод решения которой можно использовать при решении похожих задач.

Метод вспомогательной окружности

По видимому, вспомогательная окружность-одно из наиболее эстетичных дополнительных построений. Скорее всего, это связано с тем, что «увидеть» окружность там, где её нет, уже само по себе нетривиально.

Опорная задача Если в четырёхугольнике сумма противоположных углов равна 180, то вокруг него можно описать окружность.

Удлинение медианы

Во многих задачах , связанных с медианой, её удвоение или удлинение на треть приносит результат.

Задача Найти отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30 и 90.

Решение. Пусть в треугольнике ABC отрезок BM служит медианой, при этом

. Возьмем на продолжении отрезка BM точку D так, что BM = MD. Тогда треугольники ABM и CDM равны по двум сторонам и углу между ними. Значит, Поэтому треугольник BDC - прямоугольный с углом CBD , равным 30. Следовательно,

Ответ: 1:2.

Метод площадей

В основе метода площадей часто используются следующий прием: отношение отрезков расположенных на одной прямой иногда полезно заменить на отношение площадей треугольников с общей вершиной, основаниями которых являются данные отрезки.

Так же, метод площадей основан на некоторых теоремах школьного курса:

Медиана треугольника разбивает его на два равновеликих треугольника.
Отношение площадей треугольников с одинаковой высотой равно отношению их оснований.
Отношение площадей треугольников с одинаковым основанием равно отношению их высот.
Площади треугольников с одинаковым углом относятся друг к друг как произведения сторон заключающих одинаковые углы.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные прилежащим сторонам треугольника.

Задача

Дан треугольник ABC с площадью равной S. Все его стороны продолжили на их длину. Концы получившихся отрезков соединили и получился треугольник . Найти его площадь.

Решение Соединим вершины С и . В полученном треугольнике СВ – медиана значит площадь . В треугольнике - медиана значит .аналогично для двух оставшихся треугольников. т.е.