Пушкин и математика - Интегрированный урок математики и литературы 9 класс

Муниципальное общеобразовательное учреждение- средняя общеобразовательная школа №8

Пушкин и математика.

(Интегрированный урок математики и литературы в 9 классе,

посвящённый 215-летию со дня рождения А.С.Пушкина, 45минут)

Подготовили: Бочкарёва О.П.,

учитель русского языка и литературы,

1 категория.

Коныхова О.А., учитель математики,

1 категория

Аткарск, 2014

Пушкин и математика.

(Интегрированный урок математики и литературы в 9 классе, 45 минут.)

“Поверил я алгеброй гармонию”

А.С.Пушкин. «Моцарт и Сальери».

Цель урока: формирование представления у школьников о единстве школьных дисциплин в понимании целостности окружающего мира.

Показать реализацию здоровьесберегающих технологий через активизацию мыслительного процесса учащихся, создание благоприятного психологического климата урока, эмоциональной атмосферы во время работы.

ЗАДАЧИ УРОКА:

обучающие - изучить на примере произведений А.С.Пушкина стихотворные и композиционные приёмы построения текстов в художественной литературе;

научить применять математические методы анализа поэтического произведения;

развивающие - развитие творческого мышления, любознательности и познавательной активности учащихся через математизацию построения произведений А.С.Пушкина; развитие умения применять полученные знания в нестандартных ситуациях;

воспитательные - воспитание чувства национальной гордости и патриотического отношения учащихся к истории нашей Родины через изучение художественного наследия А.С.Пушкина; воспитание устойчивого интереса учащихся к жизни и творчеству А.С.Пушкина.

воспитание любви к русской речи, поэзии и математике.

Оборудование урока: учебники по алгебре и литературе, тетради, доска, раздаточный материал, мультимедиа, фонохрестоматия.

План урока.

Организационный момент.
Постановка проблемы. ( разгадав кроссворд, узнать тему урока)
Слово учителя математики. (золотое сечение)
Чтение наизусть (описание Татьяны)
Слово учителя литературы. (анализ понятия «онегинская строфа»)
Слово учителя математики. (прогрессия)
Гимнастика для глаз.( музыкальная пауза)
Слово учителя литературы. ( ямб, хорей)
Чтение наизусть отрывка из письма Онегина.
Слово учителя математики. (прогрессия)
Самостоятельная работа по литературе и математике (тесты)
Подведение итогов урока.
Домашнее задание.
Рефлексия.

Ход урока.

Организационный момент.

Учитель литературы. Добрый день ребята! Добрый день уважаемые гости! Наверное, ученики ждут, когда же из нас кто- нибудь пройдёт, присядет, и начнётся урок математики или литературы. Так? Сегодня будет всё не так. Сегодня мы с Ольгой Анатольевной будем вести урок вместе! Неожиданно? Согласна! Тем более, что вы-то уж точно знаете мой маленький секрет! Какой?( я считаю до трёх для установления тишины- это шутка такая). Начнём наш урок. У вас на партах две тетради, открываем обе и записываем число, классная работа. Что мы ещё привыкли записывать? Правильно, тему! А какая тема сегодняшнего урока, вам поможет узнать решение кроссворда. И я передаю слово Ольге Анатольевне.

2.Постановка проблемы урока.

Учитель математики. Ребята, ответив на вопросы, мы сможем определить тему нашего урока.

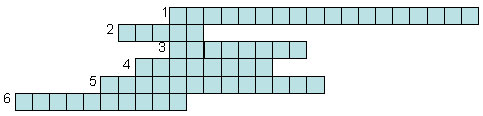
1. Одно из основных понятий математики, может быть составлено из чисел, точек, функций, векторов.

2. Последовательность считается заданной, если указан …

3. Величайший физик современности.

4. Число, с помощью которого можно получить следующий член прогрессии, зная предыдущий.

5. Способ задания последовательности с помощью формулы.

6. Последовательность, каждый член которой, начиная со второго равен предыдущему члену, сложенному с одним и тем же числом.

Какое слово у нас получилось? Правильно, поэзия.

4.Анализ «онегинской строфы».

Учитель литературы. Когда мы произносим слово «поэзия», какое имя сразу возникает у нас в голове? Умнички! Конечно же, А.С.Пушкин. А какой предмет у вас преподаёт Ольга Анатольевна? Математику! Поэтому тема нашего урока такова «А.С.Пушкин и математика». Запишите в тетради тему и эпиграф. Думаю, многие из присутствующих удивились, при чём здесь Пушкин? Когда нам объявили, что на базе нашей школы пройдёт районный семинар, и мы в нём участвуем, как учителя двух основных предметов, мы загорелись идеей показать или что-то новое или хорошо забытое старое. Вот так и родилась идея интегрированного урока. Ребята увидят, как полярные предметы могут быть взаимосвязаны между собой. А гости, мы надеемся, смогут почерпнуть для своих уроков какие-то идеи. Пушкин появился не случайно. Во-первых, это мой любимый поэт; во-вторых, в 2014 году 6 июня исполняется 215 лет со дня его рождения; в- третьих, мы изучили его роман в стихах «Евгений Онегин»; в–четвёртых, век Пушкина- это золотой век и его название связано с задачами нашего урока; в-пятых, свой урок мы начинали строить, как и Пушкин «И даль свободного романа через магический кристалл ещё не ясно различал...». Но большой роман, который задумал Пушкин, должен иметь чёткую структуру, отчётливые части. Пушкин делит роман на главы, а главы – на строфы.

5.Чтение наизусть. Давайте послушаем девочек, они подготовили чтение наизусть. О ком эти строки? Правильно, о главной героине, Татьяне Лариной.

Вы помните, что поэт создал свою «онегинскую» строфу. Она состоит из 14 строк, которые делятся на три четверостишия и заключительное двустишие с разными способами рифмовки: первое четверостишие имеет перекрёстные рифмы, второе- парные или смежные, третье- кольцевые или опоясывающие, заключительная – куплет или двустишие (они смежные). « Онегинская» строфа отличается необыкновенной гибкостью, живостью и лёгкостью. Поэт добивается такого эффекта, используя четырёхстопный ямб, придавая ему различные интонации в зависимости от содержания строф. Давайте проанализируем и посмотрим, так ли это.

Она любила на балконе а

Предупреждать зари восход, б перекрёстная

Когда на бледном небосклоне а

Звёзд исчезает хоровод, б

И тихо край земли светлеет, с

И, вестник утра, ветер веет, с парная

И всходит постепенно день. д

Зимой, когда ночная тень д

Полмиром доле обладает, е

И доле в праздной тишине, ф кольцевая

При отуманенной луне, ф

Восток ленивый почивает, е

В привычный час пробуждена г куплет или двустишие

Вставала при свечах она. г

Итак, мы можем с уверенностью констатировать тот факт, что Пушкин использовал определённый порядок при написании своего гениального романа, а не просто записывал строки в сумбурном, хаотическом нагромождении. Он продумывал каждое слово, находил для него нужное место, поэтому роман так гармоничен. Ребята, мы с вами повторили и углубили наши знания о романе. «Онегинской строфой» написан весь роман, за исключением песен крепостных девушек и писем Татьяны и Онегина.

6.Чтение наизусть. Давайте послушаем чтение наизусть отрывка из письма Онегина к Татьяне.

Случайно вас когда-то встретя,

В вас искру нежности заметя,

Я ей поверить не посмел:

Привычке милой не дал ходу;

Свою постылую свободу

Я потерять не захотел.

Ещё одно нас разлучило…

Несчастной жертвой Ленский пал…

Ото всего, что сердцу мило,

Тогда я сердце оторвал;

Чужой для всех, ничем не связан,

Я думал: вольность и покой

Замена счастью. Боже мой!

Как я ошибся, как наказан!

Нет, поминутно видеть вас,

Повсюду следовать за вами,

Улыбку уст, движенье глаз

Ловить влюблёнными глазами,

Внимать вам долго, понимать

Душой всё ваше совершенство,

Пред вами в муках замирать,

Бледнеть и гаснуть…вот блаженство!

А почему А.С.Пушкин применил такой приём, изменив рифму, мы спросим у математиков. Думаю, у них своя точка зрения.

7. Понятие о золотом сечении. Учитель математики.

Можно ли выразить красоту с помощью формул и уравнений? Есть ли на планете единый стандарт прекрасного? Возможно ли измерить гармонию с помощью циркуля и линейки? Математика дает на все эти вопросы утвердительный ответ. Золотое сечение - ключ к пониманию секретов совершенства в природе и искусстве. Именно соблюдение "божественной пропорции" - помогает художникам и поэтам достигать эстетического идеала.

История золотого сечения (сообщение ученика)

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира.

В дошедшей до нас античной литературе золотое деление впервые упоминается в “Началах” Евклида. Во 2-й книге “Начал” дается геометрическое построение золотого деления.

Учитель: В чём же заключается суть золотой пропорции? (ученик у доски, ученики в тетради)

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей;
с : b= b : а.

Рис. 1.
Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

Рис. 2. Деление отрезка прямой по золотому сечению. BC= 1/2 AB; CD= BC

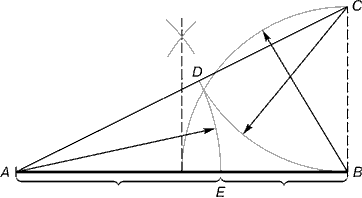
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Исследование числа Ф

Выясним, чему равно значение золотой пропорции, и какое это число - рациональное или иррациональное? Для этого воспользуемся математическими выкладками.

Точка Е делит отрезок в золотом отношении:

a — длина всего отрезка, b — длина большей его части.

Тогда имеет место пропорция:

Разделим обе части равенства на b²

обозначив отношение , получим уравнение:

Его положительный корень есть число иррациональное, приблизительно равное 1,6.

Значение золотой пропорции 1,6.

Как это число связано с романом «Евгений Онегин»?

Представляет несомненный интерес анализ романа "Евгений Онегин", сделанный Н. Васютинским. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов.

Какая глава является наиболее совершенной и эмоционально насыщенной ?

Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава. Н. Васютинский констатирует:
«Кульминацией главы является объяснение Евгения в любви к Татьяне – строка «Бледнеть и гаснуть … вот блаженство!». Эта строка делит всю восьмую главу на две части – в первой 477 строк, а во второй – 295 строк.

Вопрос: Найдите отношение 477 к 295

Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершенное гением Пушкина!»

8. Музыкальная пауза.

9. Стихотворные размеры. Учитель литературы.

Высокой страсти не имея

Для звуков жизни не щадить,

Не мог он ямба от хорея,

Как мы ни бились, отличить.

Это Пушкин пишет о своём главном герое, Евгении Онегине. Давайте вспомним законы стихосложения и стихотворные размеры стиха. Назовите их ( ямб, хорей, дактиль, анапест, амфибрахий). Назовите только двусложные, охарактеризуйте их. 80% стихов А.С.Пушкина написаны ямбом.

Ямб – ударение падает на чётные слоги, т.е на 2,4,6 и т.д.

Хорей – ударение падает на нечётные слоги, т.е. на 1,3,5 и т.п.

Определите стихотворный размер данного отрывка.

Быть можно дельным человеком

И думать о красе ногтей:

К чему бесплодно спорить с веком?

Обычай деспот меж людей.

Какой это размер? Правильно, ямб. Сколько ударных слогов в каждой строчке? Да, четыре. Это и есть четырёхстопный ямб. Именно этим размером и написан роман.

10. Прогрессия. Учитель математики. Номера ударных слогов образуют последовательность 2,4,6,8,…

Вопросы:

Как называется данная последовательность?
Скажите определение арифметической прогрессии.
Способ задания данной последовательности?
Чему равен n-член арифметической последовательности?
Назовите формулу суммы n-первых членов арифметической погрессии.

Выполните задания, связанные с прогрессией на листах. Ответы составляют год начала работы над романом «Евгений Онегин» 1823.

11. Самостоятельная работа. Учитель литературы. А сейчас, ребята, поработаем самостоятельно, посмотрим, как вы запомнили материал нашего урока. У вас на столах лежат тестовые задания, выполните их, листочки подпишите и сдайте. Самостоятельная работа по литературе. (ответ в виде теста в формате ОГЭ, в конце урока сдать)

Кокетка судит хладнокровно,

Татьяна любит не шутя

И предаётся безусловно

Любви, как милое дитя,

Не говорит она: отложим-

Любви тем цену мы умножим,

Вернее в сети заведём;

Сперва тщеславие кольнём

Надеждой, там недоуменьем

Измучим сердце, а потом

Ревнивым оживим огнём;

А то, скучая наслажденьем,

Невольник хитрый из оков

Всечасно вырваться готов.

Тест

1.Какие рифмы использует Пушкин при создании «онегинской строфы».

а) перекрёстная

б) кольцевая

в) парная

г) опоясывающая.

2. Из приведённого ниже перечня выберите 3 названия художественных средств и приёмов, использованных поэтом в данном отрывке.

а) эпитет

б) фразеологизм

в) метафора

г) сравнение

3. Что такое «онегинская строфа»?

а) строфа из 8 стихов, где первые 6 рифмуются между собой, а две связываются парной рифмовкой.

б) строфа из 14 строк, 4-стопного ямба, где 3 четверостишия, завершающиеся 2 строками с куплетной рифмой.

в) гекзаметр

г) строфа из 14 строк, написанная кольцевыми рифмами

4. Назовите стихотворный размер, использованный поэтом при создании романа «Евгений Онегин».

а) дактиль

б) хорей

в) ямб

г) анапест

12. Подведение итогов урока.

Учитель математики. Математика и поэзия… Разве может что-то их связывать? Они такие разные! Ученый древнего востока Омар Хайям писал сложные труды по математике, а на полях писал стихи. Его знаменитыми рубаями мы зачитываемся до сих пор. Великий русский геометр Н.И.Лобачевский писал стихи. В полной мере можно отнести к нему слова А.С.Пушкина: “Вдохновение нужно в поэзии, как в геометрии”. Писала стихи и женщина-математик Софья Васильевна Ковалевская, а о математике она говорила так: “Нельзя быть математиком, не будучи в тоже время поэтом в душе”.

Сегодня на уроке мы не только обобщили знания по теме “Арифметическая прогрессия”, но и нашли им практическое применение в искусстве стихосложения- чередовании ударных и безударных слогов (ритм). В основе литературного произведения лежат принципы гармонии и красоты, а, следовательно, и золотая пропорция. Это проявляется в композиционном построении произведений,в эмоциональной насыщенности и т.д.

Учитель литературы. Стихотворная речь – категория двуединая. Несомненно, она - явление литературное, эстетическое. Но столь же несомненно, что некоторые особенности стихотворной речи требуют применения математических знаний. Необходимо отметить, что литература не является наукой, это особый вид искусства, поэтому нельзя подходить к анализу художественных произведений только с точки зрения математических формул, логики. Литература часто обращается к иррациональному, субъективному, недосказанному, находя путь к уму и сердцу читателя. Гениальный человек гениален во всем. И на самом деле, не столь уж важно, в какой степени знал А.С. Пушкин точные науки. Каждый человек находит в нем и его творчестве что-то свое, близкое и понятное только ему. Даже люди, которые считают себя далекими от поэзии, от романтических переживаний, занятые только сухими расчетами в своем мире формул и чисел, и они найдут множество «открытий чудных» в мире пушкинских произведений. Но самое главное, что и в наше время А.С. Пушкин учит нас искренности чувств, жизнелюбию; ставит перед нами вечные вопросы: какое место в списке ценностей занимают милосердие, доброта, дружба, любовь.

Мы надеемся, что наш урок поможет вам понять, что наука и искусство тесно связаны, а мир так многолик, чтобы познать его нужно быть и ученым, и поэтом в душе.

Учитель математики. Отметки за урок вы получите и по литературе и по математике, когда мы проверим ваши тесты. А нашим выступающим - «отлично».

13.Домашнее задание.

По математике. Исследовательская работа числа Фибоначчи и их применение в поэзии Пушкина

По литературе. Определить стихотворный размер (дописать автора)

14.Рефлексия.

Как назывался тип сегодняшнего урока?

Как вы поняли, зачем нужны такие уроки?

Что вы уносите с урока?

Какие темы вам бы хотелось ещё обсудить? Какие предметы?

15.Заключение урока. Чтение наизусть, инсценирование.

Спор математика и филолога.

Математик:

Нет ничего важнее той науки,

что люди математикой зовут.
Что людям могут дать пустые звуки?
Писать стихи… Но разве это труд?
Филолог:

Нет ничего ужасней чисел скучных,

Каких-то формул, множества нулей.
А слово нужное? Оно ведь лечит душу,
И в трудный час нас делает сильней.
Математик:

Нет! Миром числа управляют.

Они в порядок наш приводят ум.
И истину лишь математики познают,
Как Архимед, Евклид, Паскаль и Юнг.
Филолог:

Есть листьев шум и мир под облаками.

Рассвет. Туман. Осеннее ненастье.
Числом не скажешь все, что выразишь словами -
И боль, и страх, любовь и счастье.

Математик:

Но математику учил ракет создатель,

И в космос полетели мы без вас.

Филолог:

Нет! Первым в космос полетел писатель,

Писатель тот, который был фантаст.
Учитель литературы:

Друзья мои! не надо ссор,
Не разрешить вам этот спор.

Учитель математики и филолог вместе :

Решение всего одно

И лишь в гармонии оно!

Список литературы

А.С.Пушкин. Евгений Онегин. Сочинение в 3 томах, т.2,- Москва, 1986
Учебник литературы
И.В.Золотарёва, О.Б.Беломестных, М.С.Корнеева. Поурочные разработки по литературе, 9 класс,- Москва, 2004
Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова; под редакцией С.А.Теляковского, Алгебра.
Л.В.Кузнецова, Е.А.Бунимович, Б.П.Пигарев, С.Б.Суворова. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы.
С.П.Ковалева. Алгебра, 9 класс, поурочные планы.
Н.П.Ким. Нестандартные уроки алгебры, 9 класс.
Лиман М.М. Школьникам о математике и математиках. (“Просвещение”, 1981).
Литературная энциклопедия (М., 1929-1939. Т. 1-11).
Золотой век русской поэзии (Эксмо, 2007).