Рассмотрена Утверждаю

на педсовете директор школы

Протокол № 1 __________________

от 20.08.2012 В.А. Шкарупелова

Приказ № 62-о от 03.09.12

Муниципальное бюджетное вечернее (сменное) общеобразовательное учреждение

« Михайловская районная вечерняя (сменная) общеобразовательная школа»

РАБОЧАЯ ПРОГРАММА

по математике для 9 класса

(авторская линия Ш.А. Алимова, Атанасяна Л.С)

Автор-составитель:

Меркулова Елена Валерьевна,

учитель математики

Михайловка

2012

Содержание:

Пояснительная записка _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 3с.

Планируемые результаты. Система контроля _ _ _ _ _ _ _ _ _ _ 8с.

Содержание планирования _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 16с.

Тематическое планирование _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _­_18с.

Учебно-методическое обеспечение _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 21с.

Материально-техническое оснащение _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 22с.

Пояснительная записка

Статус документа

Рабочая программа по математике для обучающихся9 класса (заочная форма) разработана в соответствии с Примерной программой основного общего образования по математике, с учётом требований федерального компонента государственного стандарта общего образования, Основана на авторской программе линииАлимов Ш.А. и Атанасян Л.С. и др.
и реализуется на основе следующих документов:

• Программы для общеобразовательных школ, гимназий, лицеев по математике 5-11 классы.

• .Стандарта основного общего образования по математике.

• Базисный учебного плана вечерних (сменных) общеобразовательных учреждений, утвержденного приказом Минобразования России (№ от 09.02.1998г. № 322).

Значение математики в школьном образовании.

Математическое образование в основной школе складывается из следующих содержательных компонентов: арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.

Алгебра. Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышле­ния, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.

Геометрия— один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, фор­мирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математи­ческой культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.

При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.

Таким образом, в ходе освоения содержания курса учащиеся получают возможность:

развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Цели изучения:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;

• развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса обучающиеся овладевают приёмами вычислений на калькуляторе.

Место предмета в федеральном базисном учебном плане.

Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится 5часов в неделю: учебный предмет «алгебра» - 3 ч в неделю, учебный предмет «геометрия» - 2 часа в неделю.

В вечерней общеобразовательной школе программа реализуется по базисному учебному плану вечерних (сменных) общеобразовательных учреждений, утвержденного приказом Минобразования России (№ от 09.02.1998г. № 322)предусматривающему на изучение математики:

9класса – 2,25 часа.Учебный курс «Математика» представлен двумя учебными предметами: «Алгебра» и «Геометрия».При этом предполагается построение курса в форме последовательности тематических блоков с чередованием материала по алгебре и геометрии. При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: Алгебра, Функции, Уравнения и неравенства, Элементы комбинаторики, теории вероятностей, статистики и логики .

Цель и задачи рабочей программы.

Данная программа конкретизирует содержание стандарта, дает распределение учебных часов по разделам курса, последовательность изучения тем и разделов с учетом межпредметных и внутрипредметных связей, логики учебного процесса, возрастных особенностей учащихся.

Основными проблемами математики являются изучение объектов математических умозаключений и правил их конструирования, вскрытие механизма логических построений, выработка умения формулировать, обосновывать и доказывать суждения, тем самым развивая логическое мышление.

Особенности данной программы

Особенность организации учебного процесса по данному курсу связана с особым контингентом обучающихся, у них: либо изначально слабые знания, либо значительный перерыв в обучении. Так как обучающие школы в значительном большинстве мало подготовлены к систематическому изучению математических дисциплин и у многих из них имеются большие пробелы в знаниях, полученных ранее, то при изучении нового материала им требуется значительное время для его закрепления. В связи с этим программа по математике составлена так, чтобы дать возможность компенсировать незнание пройденного ранее материала и облегчить изучение нового. Основной задачей повторения является приведение в систему полученных знаний. Создание полной картины пройденного материала помогает обучающемуся яснее видеть цель и результаты обучения, а также пробелы в своих знаниях. Основная роль в организации учебного процесса отводится решению задач, что служит целью и средством обучения и математического развития. Организация дифференцированного подбора задач способствует нормализации нагрузки обучающихся, обеспечивает их посильной работой и формирует положительное отношение к учёбе. Основным условием правильной организации учебного процесса является его генерализация и выбор учителем рациональной системы методов и приёмов обучения. Основная задача в работе учителя — научить обучающихся работать по образцу, т. е. выполнять различные преобразования по алгоритмам, схемам и т. п., с использованием справочной литературы

Отличительные особенности данной рабочей программы

по сравнению с примерной:

В программу внесены изменения по количеству часов на изучение следующих тем:

Раздел

Количество часов в примерной программе

Количество часов в рабочей программе

Самостоятельное изучение

1. Алгебраические уравнения. Системы нелинейных уравнений

22

12

10

2. Векторы

8

5

3

3. Степень с целым показателем

10

6

4

4. Метод координат

10

6

4

5. Степенная функция

18

10

8

6. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

10

7

3

7. Элементы тригонометрии

7

7

-

8. Длина окружности и площадь круга. Движения

20

8

12

9.Прогрессии

16

7

9

10. Начальные сведения из стереометрии

10

5

5

11. Элементы комбинаторики

6

3

3

12. Повторение курса математики за основную школу

10(г)+23(а)

5

28

ИТОГО

170

81

89

Планируемые результаты. Система контроля.

Ожидаемый результат.

Результаты изучения курса приведены в разделе «Требования к уровню подготовки обучающихся», который полностью соответствует стандарту. Требования направлены на реализацию компетентностного, практикоориентированного и личностно ориентированного подходов; освоение учащимися интеллектуальной и практической деятельности; овладение знаниями и умениями, востребованными в повседневной жизни, науке и технике, позволяющими ориентироваться в окружающем мире и необходимые для трудовой и профессиональной подготовки обучающихся.

ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ

ПО ДАННОЙ ПРОГРАММЕ

Ученик долженврезультате изучения:

алгебры

знать/понимать:

• существо понятия математического доказательства; приводить примеры доказательств;

• существо понятия алгоритма; приводить примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов.

Уметь:

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• решать квадратные уравнения и рациональные уравнения, сводящиеся к ним;

• решать линейные и квадратные неравенства с одной переменной и их системы;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;

• распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем;

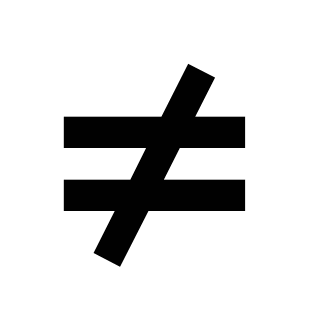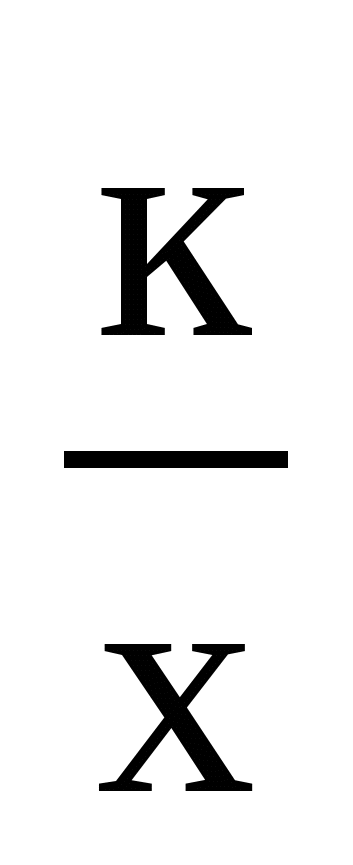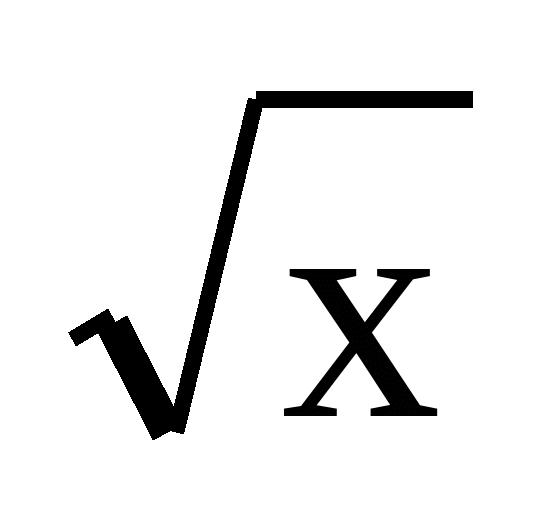• описывать свойства изученных функций (у=кх, где к0, у=кх+b, у=х², у=х³, у =, у=, у=ах²+bх+с, у= ах²+n у= а(х- m) ²), строить их графики

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

Арифметики

Уметь:

• выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;

• записывать большие и малые числа с использованием целых степеней десятки;

• выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с натуральными показателями; находить значения числовых выражений;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;

• устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.

Элементы логики, комбинаторики, статистики и теории вероятностей

Уметь:

• проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

• решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;

• вычислять средние значения результатов измерений;

• находить частоту события, используя собственные наблюдения и готовые статистические данные;

• находить вероятности случайных событий в простейших случаях;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выстраивания аргументации при доказательстве и в диалоге;

• распознавания логически некорректных рассуждений;

• записи математических утверждений, доказательств;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих систематического перебора вариантов;

• сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;

• понимания статистических утверждений.

Геометрии:

В ходе преподавания геометрии в 9 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

• планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

• решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

• исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

• ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

• проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

• поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

знать/понимать:

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

уметь:

• пользоваться языком геометрии для описания предметов окружающего мира;

• распознавать геометрические фигуры, различать их взаимное расположение;

• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;

• распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;

• в простейших случаях строить сечения и развертки пространственных тел;

• проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;

• вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;

• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

• решать простейшие планиметрические задачи в пространстве;

использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:

• описания реальных ситуаций на языке геометрии;

• расчетов, включающих простейшие тригонометрические формулы;

• решения геометрических задач с использованием тригонометрии

• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Система контроля

При изучении курса проводится 2 вида контроля:

текущий – контроль в процессе изучения темы;

формы: устный опрос, тестирование, самостоятельные работы, контрольные работы

итоговый – контроль в конце изучения зачетного раздела;

формы: устные и письменные зачетные работы по отдельным темам, собеседование, практические работы.

Формы занятий:

1. групповая консультация

2. индивидуальная консультация

3. зачет.

Типы индивидуальных консультаций

1. Выявление и ликвидация пробелов в знаниях обучающихся

2. Подготовка к изучению нового материала

3. Решение задач практического содержания

4. Подготовка к контрольной работе

Формы и методы проведения зачета:

1. Устно-индивидуальный опрос по карточкам-заданиям

2. Тест

3. Групповое собеседование

4. Письменный зачет

5. Устно-письменный зачет

6. Письменные ответы на вопросы

Формы промежуточной и итоговой аттестации: промежуточная аттестация проводится в форме тестов, контрольных, самостоятельных работ. Итоговая аттестация предусмотрена в виде административной контрольной работы или административного итогового теста.

Уровень обучения – базовый.

Критерии и нормы оценки знаний, умений и навыков

обучающихся по математике.

1. Оценка письменных контрольных работ

обучающихся по математике.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2.Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

• ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• неумение пользоваться первоисточниками, учебником и справочниками;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

3.2. К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

• нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

Содержаниепланирования.

Алгебра.

1. Повторение материала 8 класса

Повторение пройденного материала, обобщение и систематизация.

2. Алгебраические уравнения. Системы нелинейных уравнений.

Деление многочленов. Решение алгебраических уравнений. Уравнения, сводящиеся к алгебраическим. Различные способы решения систем уравнений. Решение задач с помощью систем уравнений.

Цель: ознакомить обучающихся с приемами решения некоторых алгебраических уравнений, выработать умение решать простейшие системы нелинейных уравнений и применять их при решении задач.

3. Степень с целым показателем .

Степень с целым показателем и ее свойства. Возведение числового неравенства в степень с натуральным показателем. Арифметический корень n-ой степени.

Цель: сформировать поняьтие степени с целым показателем; выработать умение выполнять преобразования простейших выражений, содержащих степень с целым показателем.

4. Степенная функция

Область определения и свойства функции. Возрастание и убывание функции. Четность и нечетность функции. Функция у=к/х. Степенная функция.

Цель: выработать умение устанавливать основные свойства (читать график) по заданному графику функции у=х², у=х³, у=1/х,у =, у=, у=ах²+bх+с и изображать эскизы графиков этих функций.

5. Прогрессии

Числовые последовательности, способы задания, свойства. Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых nчленов арифметической и геометрической прогрессии.

Цель: позанкомить обучающихся с понятиями арифметической и геометрической прогрессий.

6.Элементы тригонометрии

Радианная мера угла. Определние синуса, косинуса, тангенса угла. Знаки синуса, косинуса, тангенса. Зависимость между синусом, косинусом, тангенсом одного и того же угла.Формулы приведения

Цель: в ознакомительной форме познакомить обучающихся о новой мере угла, угле поворота точки вокруг анчала координат, понятиях синуса, косинуса и тангенса.

Геометрия

1. Векторы. Метод координат.

Понятие вектора. Абсолютная величина и направление вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простей­шие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.

Цель: научить обучающихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач.

2. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов.

Синус, косинус и тангенс угла. Теоремы синусов и косину­сов. Решение треугольников. Соотношение между сторонами и углами треугольника.

Цель: развить умение обучающихся применять тригонометрический аппарат при решении геометрических задач,познакомить с основными алгоритмами решения произвольных треугольников.

3. Длина окружности и площадь круга.

Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.

Цель: расширить знание обучающихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления.

4. Движения.

Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. На­ложения и движения.

Цель: познакомить обучающихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений.

5. Начальные сведения из стереометрии.

Предмет стереометрии. Геометрические тела и поверхности. Многогранники: призма, параллелепипед, пирамида» формулы для вычисления их объемов. Тела и поверхности вращения: ци­линдр, конус, сфера, шар, формулы для вычисления их площа­дей поверхностей и объемов.

Цель: дать начальное представление телах и поверхностях в пространстве; познакомить обучающихся с основ­ными формулами для вычисления площадей; поверхностей и объ­емов тел.

Тематическое планирование

№ урока

Тема

Тип урок

Дом.задание

БЛОК № 1 «Алгебраические уравнения. Системы нелинейных уравнений» (12ч)

1/1

Поворение материала за курс 8 класса

Комбинир урок

Карточка-собеседник

2/2

Тестирование на начало учебного года

Контроль знаний

3/3

Алгебраические уравнения.Системы уравнений.

Урок-практикум

Опорный конспект

4/4

Практикум. Деление многочленов.

Урок-практикум

$1, карточка собеседник

5/5

Практикум. Решение алгебраических уравнений.

Урок-практикум

$2, карточка собеседник

6/6

Практикум . Решение уравнений, сводящимся к алгебраическим.

Урок-практикум

$3, карточка собеседник

7/7

Практикум. Системы нелинейных уравнений с двумя неизвестными

Урок-практикум

$4, карточка собеседник

8/8

Практикум . Различные способы решения систем нелинейных уравнений

Урок-практикум

$5, карточка

9/9

Практикум Решение задач с помощью систем уравнений

Урок-практикум

$6, карточка

10/10

Обобщение и систематизация по теме «Алгебраические уравнения»

Комбинир урок

$ 1-6, карточка-собеседник

11/11

Урок- консультация по теме «Алгебраические уравнения»

Комбинир урок

Опорный конспект

12/12

Контрольная работа по теме «Алгебраические уравнения»

Контроль знаний

Зачет № 1 по теме«Алгебраические уравнения. Системы нелинейных уравнений»

БЛОК № 2 «Векторы»(5ч)

1/13

Понятие вектора. Сложение и вычитание векторов. Умножение вектора на число

лекция

Глава 9, $1-3, опорный конспект

2/14

Практикум.Понятие вектора. Равенство векторов»

Урок-практикум

$1, карточка

3/15

Практикум. Сложение и вычитание векторов»

Урок-практикум

$2, карточка

4/16

Практикум. Умножение вектора на число.Применение векторов»

Урок-практикум

$ 3, Карточка-собеседник

5/17

Контрольная работа по теме «Векторы»

Контроль знаний

БЛОК № 3 «Степень с рациональным показателем» (6ч)

1/18

Степень с рациональным показателем.

лекция

$7-11, олпорный конспект

2/19

Практикум «Степень с целым показателем»

Урок-практикум

$7, карточка

3/20

Практикум «Арифметический корень натуральной степени. Свойства арифметического корня»

Урок-практикум

$8,9, карточка

4/21

Практикум.Степень с рациональным показателем. Возведение в степень числового неравенства»

Урок-практикум

$10,11, карточка

5/22

Урок-консультация по теме «Степень с рациональным показателем»

Комбинир урок

Карточка-собеседник

6/23

Контрольная работа по теме «Степень с рациональным показателем»

контроль

БЛОК № 4 «Метод координат» (6ч)

1/24

Координаты вектора.Простейшие задачи в координатах.Уравнения окружности и прямой

лекция

Глава 10, опорный конспект

2/25

Практикум.Координаты вектора

Урок-практикум

$1,карточка

3/26

Практикум.Простейшие задачи в координатах.

Урок-практикум

$2,карточка

4/27

Практикум. Уравнения окружности и прямой

Урок-практикум

$3, карточка

5/28

Урок-консультация по «Метод координат»

Комбинир урок

Глава 10, Карточка-собеседник

6/29

Контрольная работа по теме «Метод координат»

Контроль знаний

Зачет № 2 по теме «Векторы. Метод координат»

БЛОК № 5 «Степенная функция» (10ч)

1/30

Степенная функция

лекция

$12-16, опорный конспект

2/31

Практикум.Область определения функции

Урок-практикум

$12, карточка

3/32

Практикум.Возрастание и убывание функции.

Урок-практикум

$13, карточка

4/33

Практикум.Четность и нечетность функции.

Урок-практикум

$14, карточка

5/34

Практикум. Функция у =k/x

Урок-практикум

$15, карточка

6/35

Практикум. Неравенства и уравнения, содержащие степень

Урок-практикум

$16, карточка

7/36

Практикум. Неравенства и уравнения, содержащие степень

Урок-практикум

$16, карточка

8/37

Обобщение и систематизация по теме «Степенная функция»

Комбинир урок

$12-16 карточка-собеседник

9/38

Урок- консультация по теме«Степенная функция»

Комбинир урок

$12-16, карточка-собеседник

10/39

Контрольная работа по теме «Степенная функция»

Контроль знаний

Зачет № 3 по теме «Степень с рациональным показателем. Степенная функция»

БЛОК № 6 «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов» (7ч)

1/40

Синус, косинус, тангенс угла. Скалярное произведение векторов. Соотношения между сторонами и углами треугольника

лекция

Глава 11, $1-3, опорный конспект

2/41

Практикум. Синус, косинус, тангенс угла.

Урок-практикум

$1, карточка

3/42

Практикум. Соотношения между сторонами и углами треугольника.

Урок-практикум

$2, карточка

4/43

Практикум. Скалярное произведение векторов

Урок-практикум

$3, карточка

5/44

Обобщение и систематизация по теме «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов»

Комбинир урок

Глава 11,$1-3, карточка-собеседник

6/45

Урок- консультация по теме«Соотношения между сторонами и углами треугольника. Скалярное произведение векторов»

Комбинир урок

Глава 11,$1-3, карточка-собеседник

7/46

Контрольная работа по теме«Соотношения между сторонами и углами треугольника. Скалярное произведение векторов»

Контроль знаний

БЛОК № 7 «Элементы тригонометрии» (7ч)

1/47

Элементы тригонометрии

лекция

$17-26, опорный конспект

2/48

Практикум. Радианная мера угла.Поворот точки вокруг начала кординат.

Урок-практикум

$17-18, карточка

3/49

Практикум. Определение синуса, косинуса и тангенса угла.Знаки синуса, косинуса и тангенса угла.

Урок-практикум

$19-21, карточка

4/50

Практикум. Тригонометрические тождества.Формулы сложения

Урок-практикум

$22-25, карточка

5/51

Практикум. Формулы приведения

Урок-практикум

$26, карточка

6/52

Урок-консультация по теме «Элементы тригонометрии»

Комбинир урок

$17-26, карточка-собеседник

7/53

Контрольная работа по теме «Элементы тригонометрии»

Контроль знаний

БЛОК № 8 «Длина окружности и площадь круга. Движения» (8ч)

1/54

Правильные многоугольники.Длина окружности и площадь круга.

лекция

Глава 12, $1-2, опорный конспект

2/55

Практикум.Правильные многоугольники

Урок-практикум

$1, карточка

3/56

Практикум. Длина окружности и площадь круга

Урок-практикум

$2, карточка

4/57

Движения

Урок-практикум

Глава 13, $1-2, опорный конспект

5/58

Практикум. Понятие движения.

Урок-практикум

$1, карточка

6/59

Практикум. Параллельный перенос и поворот

Урок-практикум

$2, карточка

7/60

Урок-консультация по теме «Длина окружности и площадь круга. Движения»

Комбинир урок

Глава 12-13, $1-2, карточка-собеседник

8/61

Контрольная работа по теме «Длина окружности и площадь круга. Движения»

Контроль знаний

БЛОК № 9 «Прогрессии» (7ч)

1/62

Прогрессии.

лекция

$27-32, опорный конспект

2/63

Практикум. Числовая последовательность.

Урок-практикум

$27, карточка

3/64

Практикум. Арифметическая прогрессия. Сумма п-первых членов арифметической прогрессии.

Урок-практикум

$28-29, карточка

4/65

Практикум. Геометрическая прогрессия. Сумма п-первых членов арифметической прогрессии.

Урок-практикум

$30-31, карточка

5/66

Практикум. Бесконечно убывающая геометрическая прогрессия.

Урок-практикум

$32, карточка

6/67

Урок-консультация по теме «Прогрессии»

Комбинир урок

$27-32, карточка-собеседник

7/68

Контрольная работа по теме «Прогрессии»

Контроль знаний

Зачет № 4 по теме «Прогрессии.Элементы тригонометрии»

БЛОК № 10 «Начальные сведения из стереометрии» (5ч)

1/69

Многогранники. Тела и поверхности вращения

лекция

Глава 14, $1-2, опорный конспект

2/70

Практикум. Многогранник. Призма. Параллелепипед

Урок-практикум

$1, карточка

3/71

Практикум. Объем тела.Свойства прямоугольного параллелепипеда.Пирамида.

Урок-практикум

$1, карточка

4/72

Практикум. Тела и поверхности вращения

Урок-практикум

$3, карточка-собеседник

5/73

Контрольная работа по теме «Многогранники. Тела и поверхности вращения»

Контроль знаний

Зачет № 5 по теме « Длина окружности и площадь круга. Начальные сведения из стереометрии

БЛОК № 11 «Элементы комбинаторики» (3ч)

1/74

Элементы комбинаторики и теории вероятности

лекция

Опорный конспект

2/75

Практикум. Начальные сведения из теории вероятности.Элементы комбинаторики.

Урок-практикум

Карточка-собеседник

3/76

Контрольныйсрез по теме «Элементы комбинаторики»

Контроль знаний

БЛОК № 12 Повторение курса математики за основную школу (5ч)

1/77

Повторение. Уравнения и неравенства. Системы уравнений и неравенств

Комбинир урок

Карточка-собеседник

2/78

Повторение.Решение задач с помощью уравнений и систем уравнений

Комбинир урок

Карточка-собеседник

3/79

Повторение. Алгебраические выражения

Комбинир урок

Карточка-собеседник

4/80

Повторение. Треугольники. Четырехугольники

Комбинир урок

Карточка-собеседник

5/81

Итоговое тестирование за курс основной школы

Контроль знаний

Учебно-методическое обеспечение

Учебники:

• Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. ­- М.: Просвещение, 2010. - 287 с.

• Геометрия: учеб, для 7—9 кл. / [Л. С. Атанасян, В. Ф. Бутузов, С. В. Кадомцев и др.]. — М.: Просвещение, 2010.

Литература для учителя

• Вероятность и статистика. 5–9 кл.: пособие для общеобразоват. учеб. заведений / Е.А. Бунимович, В.А. Булычев. – М.: Дрофа, 2005. – 159 с.: ил.

• Дидактические материалы по алгебре для 9 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. – М.: Просвещение, 2009. – 141 с.: ил.

• Алгебра. 9 класс. Самостоятельные и контрольные работы / О.Л. Безрукова. / Волгоград: Учитель, 2008. – 160 с.

• Алгебра. 9 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г. Мордковича. - М.: Мнемозина, 2010. – 112 с.

• Алгебра.9 класс. Контрольные работы: учебное пособие для общеобразовательных учреждений / Ю.П. Дудницын, Е.Е. Тульчинская; под ред. А.Г. Мордковича. - М.: Мнемозина, 2011. – 48 с.

• Тесты по алгебре: 9 класс / Е.М. Ключникова, Н.В. Комиссарова. – М.: Издательство «Экзамен», 2010. – 94 с.

• Алгебра. 7-9 классы. Тесты для учащихся общеобразовательных учреждений / А.Г. Мордкович, Е.Е. Тульчинская, - М.: Мнемозина, 2008. – 119 с.: ил.

• Зив Б. Г. .Геометрия: дидакт. материалы для 9 кл. / Б. Г. Зив, В. М. Мейлер. — М.: Просвещение, 2010.

• Изучение геометрии в 7, 8, 9 классах: метод, рекомендации: кн. для учителя / [Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков и др.]. - М.: Просвещение, 2009

Материально-техническое оснащение

Мультимедиа: Уроки алгебры 9 класс / Виртуальная школа Кирилла и Мефодия

Набор таблиц для изучения разделов по курсу математики 9 кл.

Модели геометрических фигур

.