Министерство образования Московской области

Государственное образовательное учреждение

начального профессионального образования

Профессиональное училище № 6

Учебно – практическая конференция

Тема:

«Математика и оборона»

(проект, посвященный 65 – летию Победы в Великой Отечественной войне)

Подготовила:

преподаватель математики ПУ № 6

Соколова Л.М.,

Коломна 2010 г.

ПЛАН

Вступление.

1. Начало использования математических знаний в военном деле.

2. Теория стрельбы.

3. Совершенствование военной техники.

4. Практические задачи:

- Как поступил сержант.

- Когда фашисты посягнули на нашу землю.

- Хлеб войны.

5. Успехи в кораблестроении.

6. Статистический контроль в военном производстве.

7. Разработка ядерного оружия.

8. Создание вычислительной техники.

Заключение.

Вступление.

Ребята!

9 мая мы будем отмечать знаменательную дату в истории нашей страны – 65 – летие победы в Великой отечественной войне.

В канун этого праздника учащиеся I – II курсов работали над проектом «Математика и оборона». Ребята собирали материал о вкладе ученых – математиков дело победы советского народа над сильным и коварным врагом. Этот вклад состоит в использовании тех специфических знаний, которыми обладают математики.

Сегодня мы проводим учебно – практическую конференцию, входе которой будут сделаны сообщения о том, как резко возросло значение науки, в том числе математики, в обороне страны.

Цель нашего мероприятия:

1.Отметить вклад советских ученых – математиков в укрепление обороноспособности нашей страны.

2. Показать практическое применение математических задач для фронта и тыла.

3. Воспитать у учащихся интерес к предмету и любовь к своей Родине.

И, наконец, желаю всем вам по-новому оценить значение предмета математики в жизни.

1. Начало использования математических знаний

в военном деле.

Начало использования математических знаний в военном деле относится к глубокой древности. Известно, что в Древнем Вавилоне арифметические сведения употреблялись при подсчете необходимых запасов для армии, геометрия же использовалась при строительстве укреплений и подсчете подъема необходимых земляных работ.

В знаменитом диалоге Платона «Государство» говорится о том, что арифметика и геометрия необходима каждому воину. Вот небольшие цитаты из текста диалога: «Но ведь арифметика и счет целиком касаются числа?..

- Значит, они принадлежат к тем познаниям, которые мы искали. Воину их необходимо усвоить для войскового строя, а философу - для постижения сущности...»

«При устройстве лагерей, занятии местностей, стягивания и развертывания войск и разных других построениях, как во время сражения, так и в походах, конечно, скажется разница между знатоком геометрии и тем, кто её не знает».

С глубокой древности в военном деле применялись различные способы передачи информации, в том числе и такие, которые недоступны для понимания противником.

История использования различного рода кодов для шифровки сообщений насчитывает тысячелетия. Вспомним, что математику Ф. Вситу (1540-1603) удавалось с большой легкостью разгадывать шифры, использовавшиеся испанским королем для передачи секретных сведений, направляемых посланнику при французском дворе и некоторым другим лицам.

Само собой разумеется, что эти вопросы в наши дни заняли несравненно большее значение. В последние десятилетия к проблемам шифрования и дешифрования широко привлекаются математики, особенно специалисты в области комбинаторики, алгебры.

Для pешения проблем обороны страны еще перед Великой Отечественной войной начали широко использоваться математические методы. Если говорить о тех направлениях математической мысли, которые нашли особенно серьезные применения, то в первую очередь следует назвать теорию дифференциальных уравнений, теорию вероятностей, алгебру и математическую логику, методы приближенных вычислений. Из прикладных математических дисциплин должны быть упомянуты теоретическая механика, гидродинамика, теория упругости, математическая физика.

Но мы не должны упускать из вида и другой аспект использования математики - ее непременное присутствие при образовании офицера армии и флота. Без математики, без ее безукоризненного знания не может быть ни хорошего штурмана, ни связиста, ни приемщика военной продукции на заводах.

Создание математического анализа - дифференциального и интегрального исчислений - в значительной мере было связано с задачами, выдвинутыми артиллерией, и что позднее, в свою очередь, развитие новой математики оказывало огромное влияние на прогресс

самой артиллерии. Во все времена считалось, что артиллерийский офицер одновременно является хорошим знатоком математики.

Для создания Советской армии необходимо было наряду с подготовкой командного состава, преданного делу октябрьской революции, решить ряд научных и инженерно – технических проблем. Проблемы артиллерии по-прежнему оставались решающими. Но наряду с ними появились задачи, связанные созданием собственной авиации, организацией радиосвязи. Они требовали не только привлечения известных и уже хорошо разработанных методов математических, но и создания новых методов исследования.

Традиционная область деятельности ученых нашей страны – исследование артиллерийских систем.

Этим занимались М. В. Остроградский (1801 —1862) и П. JI. Чебышёв (1821—1894), и последующие поколения ученых. Проблемы пристрелки, разработанные еще в XIX веке в связи с появлением новых типов артиллерии, потребовали в период Великой Отечественной войны дополнительных исследований и составления таблиц.

2. Теория стрельбы.

Во время Великой Отечественной войны широкое употребление при стрельбе по танкам и другим целям получили так называемые кумулятивные снаряды. Их пробивное действие оказалось несравненно большим, чем снарядов такого же калибра, и даже с большим количеством взрывчатых веществ. Оказывается, что если в снаряде сделать выемку и эту выемку закрыть стальным конусом, то пробивное действие такого заряда резко увеличивается. Это явление было замечено еще во 2-ой половине прошлого века и тогда же нашло использование горного дела. Первое военное применение этого эффекта относится к 1914г., широкое же использование пришлось на войну 1941-45 гг. Этом явлением заинтересовался выдающийся советский математик и механик М. А. Лаврентьев (род. в 1900 г.). После длительных экспериментов он разработал математическую теорию кумулятивного заряда.

Оказалось» что при моделировании этого явления можно воспользоваться аналогией с идеальной жидкостью. Выяснилось, что стальной конус при ударе о воду с огромной скоростью превращается в тонкую направленную струю и, как иголка, пронзает броню. При соответствующих подборах угла конуса можно получить скорость струи до 90 км/ч. С этой теорией М. А. Лаврентьева можно познакомиться по его статье «Кумулятивный заряд и принципы его работы». Большое усилие Лаврентьев потратил на использование кумулятивного эффекта для разработки теории направленных взрывов при устройстве плотин и пр. С помощью такого взрыва была построена плотина, защитившая Алма-Ату и каток Медео от селя. Теория Лаврентьева позволила не только использовать подмеченное опытным путем явление, а рассчитывать заранее его действие и при заданном усилии добиваться максимально возможного результата.

В период Великой Отечественной войны было широко использовано реактивное оружие. В качестве занимательного средства ракеты появились еще в X в. Первые боевые ракеты в России были изготовлены в 1815 г. по проекту генерала А. Д. Засядько. Они с успехом применялись в период русско-турецкой войны 1828-1829 гг., а позднее в Крымской войне 1853 - 1856 гг. В настоящее время ракетное оружие является наиболее опасным. Его действие распространяется на тысячи километров.

Известно, что еще К. Э. Циолковский много занимался ракетной техникой. Им были предложены методы расчета движения ракет. Его результаты были использованы при создании знаменитых советских «катюш». Таким образом, появлению на фронтах ракетного оружия предшествовала огромная работа не только конструкторской мысли, но и мысли математиков.

3. Совершенствование военной техники.

В период Великой Отечественной войны техника была разнообразной и сложной. Она также требовала широкого использования математических расчетов для ее изготовления и эксплуатации. Увеличение скорости полета самолетов требовало не только повышения мощности двигателей, но и выбора оптимального профиля фюзеляжа и крыльев, а также решения дрогах других вопросов.

В России над этими вопросами еще с прошлого века работал ряд ученых И В первую очередь Н. Е. Жуковский (1847 — 1921), названный В,И. Лениным отцом русской авиации. Он закономерно считается основоположником новой математической науки — аэродинамики, в которой ему удалось создать ряд сильных методов исследования и решить многочисленные актуальные задачи, основать большую научную школу, состоящую из ближайших учеников по университету и старейшему высшему техническому заведению Москвы — Московскому высшему техническому училищу.

Жуковский заложил основы Военно-воздушной академии, получившей впоследствии его имя, а также Центральный аэрогидродинамический ин­ститут. Это научное учреждение долгие годы работало под руководством одного из ближайших учеников и сотрудников Н.Е. Жуковского — С.А. Чаплыгина (1869—1942) и объединили многих выдающихся исследователей — М. В. Келдыша (1911 - 1978). В.В. Голубева (1884 - 1954), М.А. Лаврентьева (1900 - 1980) и др. Теоретический отдел разрабатывал многие важные проблемы, в том числе и для военной авиации. Многие из этих разработок пригодились и были, широко использованы для создания новых систем истребителей, штурмовиков и бомбардировщиков, обладавших повышенной маневренностью, скоростью, надежностью.

Большое значение получили теории двух явлений — штопора и шимми (или флаттера), представлявших в ту пору основную опасность для авиаторов. Как правило, самолет, попавший в состояние штопора или шимми (особые вибрации самолета, приводившие к его разрушению) уже не могли из него выйти. Теорию этих явлений создал М. В. Келдыш (впоследствии президент Академии наук СССР, главный теоретик космонавтики). Однако он пошел дальше и на основании теории сделал заключения о том, как устранять эти явления. В результате практика полетов получила надежное средство для борьбы с шимми и штопором и за все время войны практически не было в нашей авиации гибели самолетов и летчиков по этим причинам. Переоценить результаты этих исследовании невозможно, поскольку они помогли не только сохранить жизнь летчиков и самолеты, но и позволили летать на больших скоростях.

Большое значение приобрели вопросы устойчивости движения. Военное дело потребовало широкого привлечения ряда новых методов математики, в частности теории устойчивости движения, начало которой было положено еще в прошлом веке А. М. Ляпуновым (1857-1918). Он разрабатывал эту теорию в связи с задачами устойчивости солнечной системы. Но в науке часто случается, что математические приемы, созданные для определенной задачи практики, находят позднее многочисленные новые применения, и в том числе в областях знания, очень далеких от первоначальной.

Чтобы поднять самолет в воздух, требуется создать легкую и одновременно прочную конструкцию корпуса и фюзеляжа. Вот почему большое значение для авиации, а так же для морского дела получила проблема создания прочных и одновременно легких и тонких конструкций. Для её решения необходимы не только физические эксперименты, но и математические расчеты, а также создание математических моделей, интересующих нас явлений.

Стрельба с самолета по самолету и по наземным целям также привела к математическим задачам, которые нужно было срочно решить. Ими занимались упорно как специалисты в области артиллерии, так и математики. Проблемы бомбометания привели к необходимости составления таблиц, позволяющих находить оптимальное время для сброса бомб на цель, область, которую накроет бомбовой удар. Такие таблицы были составлены еще до начала войны, но для самолетов, об­ладающих большими скоростями. Во время войны выявилась полезная возможность использования тихоходных учебных самолетов для ночных бомбежек. Были созданы специальные полки ночных бомбардировщиков, но для них не было своевременно создано таблиц бомбометания. Возникла срочная задача производства соответствующих расчетов. Таблицы были созданы и они оказали несомненную помощь нашим летчикам и летчицам.

4. Практические задачи:

Во время войны, помимо решения серьезных, глобальных проблем, военным, да и гражданскому населению, часто приходилось попадать в ситуации, решение которых требовало знаний по математике.

Задача № 1.

«Как поступил сержант».

Это было на одном из фронтов Великой Отечественной войны. Подразделению лейтенанта Иванюк было приказано построить мост через горную реку. На противоположном берегу засели фашисты. Для разведки места по­стройки моста лейтенант выделил разведыватель­ную группу во главе со старшим сержантом По­повым ... В ближайшем лесном массиве они изме­рили диаметр и высоту наиболее типичных де­ревьев и подсчитали ко­личество деревьев, которые можно было использовать для постройки.

Высоту деревьев определяли при помощи вешки (шеста) так, как показано на рис. 1.

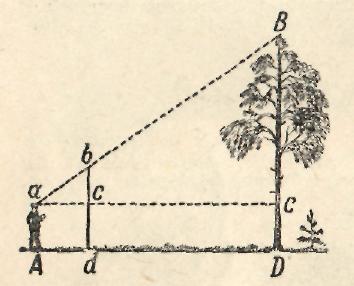
Рис. 1. Измерение высоты дерева при помощи шеста.

Этот способ состоит в следующем.

Запасшись шестом выше своего роста, воткните его в землю отвесно на некотором расстоянии от измеряемого дерева (рис. 1). Отойдите от шеста назад, по продолжению Dd до того места А, с которого, глядя на вершину дерева, вы увидите на одной линии с ней верхнюю точку b шеста. Затем, не меняя поло­жения головы, смотрите по направлению горизонтальной прямой аС, замечая точки с и С, в которых луч зрения встречает шест и ствол. Попросите помощника сделать в этих местах пометки, и наблюдение окончено. Остается только на основании подобия треугольников аbс и аВС вычислить ВС из пропорции

,

откуда

.

Расстояния bс, аС и ас легко измерить непосредственно. К полученной величине ВС нужно прибавить расстояние CD (которое также измеряется непосредственно), чтобы узнать искомую высоту дерева.

Для определения количества деревьев старший сержант приказал солдатам измерить площадь лесного массива. Затем он подсчитал количество деревьев на небольшом участке раз­мером 50×50 кв. м и произвел соответствующее умножение.

На основании всех данных, собранных разведчиками, ко­мандир подразделения установил, где и какой мост нужно строить. Мост построили к сроку, боевое задание было вы­полнено успешно.

Задача № 2.

«Когда фашисты посягнули на нашу землю».

В то время в городах, близких к фронту, приходилось делать светомаскировку. Как-то в одной из квартир, когда пришла пора затемнять окна, не нашли шторы для квадратного окна размером 120*120 см². Под рукой ничего не оказалось, кроме прямоугольного листа фанеры, площадь которого равнялась площади окна, но размеры были не те: 90*160 см². Сначала все растерялись, но прошло немного времени и школьник Вася, вооружившись линейкой, начал быстро расчерчивать прямоугольный лист фанеры. Он разрезал лист всего лишь на 2 части, из которых составил квадратный щит нужного размера для затемнения окна.

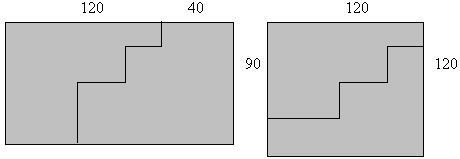
Задача № 3.

Великая Отечественная война началась 22 июня 1941 года. Узнать, сколько дней продолжалась война, поможет вам удивительный квадрат. Выберите из каждой строки и каждого столбца по одному числу, найдите сумму выбранных четырех чисел, и вы получите ответ на вопрос.

Например:

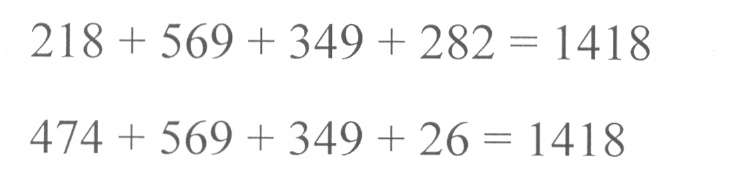
Задача № 4.

«Скорость пушечных снарядов»

Волны, наподобие сейчас рассмотренных, порождаются в воздухе летящею пулей или артиллерийским снарядом.

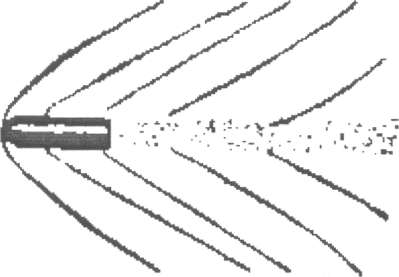
Существуют способы фотографировать снаряд налету; на рис, 1 и 2 воспроизводятся два таких изображения снарядов, движущихся неодинаково быстро. На обоих рисунках отчетливо видна интересующая нас «головная волна» (как ее в этом случае называют). Происхождение ее такое же, как и килевой волны парохода. И здесь применимы те же геометрические отношения, а именно: синус половины угла расхождения головных волн равен отношению скорости распространения волнения в воздухе к скорости полета самого снаряда.

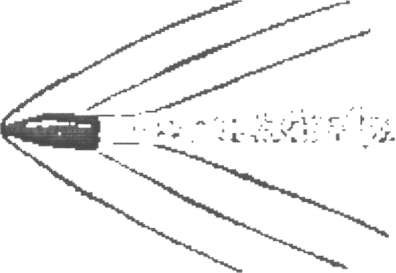
Вы видите, что довольно простые геометрические соображения при некоторой поддержке со стороны физики помогли нам разрешить задачу, на первый взгляд очень замысловатую: по фотографии летящего снаряда определить его скорость в момент фотографирования. (Расчет этот, однако, лишь приблизительно верен, так как здесь не принимаются в соображение некоторые второстепенные обстоятельства.)

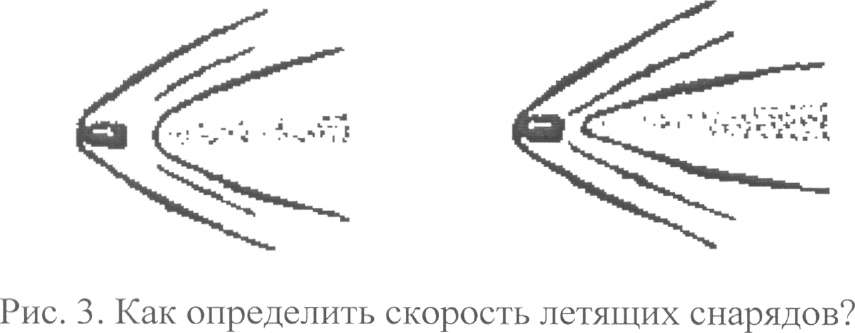
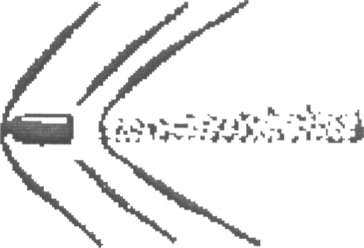
Задача № 5

Для желающих самостоятельно выполнить подобное вычисление скорости ядер здесь даются три воспроизведения снимков снарядов, летящих с различной скоростью (рис. 3).

Хлеб войны.

Главным богатством нашей Родины является хлеб. И пышный каравай и буханка душистого ржаного хлеба, и сдобная булочка – итог работы сотен тысяч людей.

В ломтике хлеба – нелегкий труд тружеников села. Это бессонные ночи железнодорожников, мукомолов, хлебопеков.

Нельзя не назвать и конструкторов, машиностроителей, которые создали технику для села.

Хлеб – мерило всех ценностей, источник жизни, труда, благополучия и радости. Хлебом-солью встречают гостей. Мы должны ценить хлеб, бережно относиться к нему.

Настоящую цену хлеба понимаешь тогда, когда его мало, не хватает. Вы изучаете много произведений, где говорится, как голодали люди во время засухи, во время войны. Хлеб войны. Каким он был? Об этом говорится в стихотворении Владимира Гордейчева “Хлеб войны”.

Хлеб войны.

Не было муки.
Она была
более легендою, чем былью,
с лебедою смешанною пылью,
черная – и все-таки бела.
Чем еще ей было нас кормить,
матери, спасавшей нас от смерти?
Это было творчеством, поверьте,
тесто из муки такой творить.
Дня не знала. Ночи не спала.
А уж сколько свеклы перетерла…
Все переборола. Не дала,
чтобы смерть схватила нас за горло.
Завывает вьюга за стеной,
белые сугробы наметая.
Вот она сидит передо мной,
женщина воистину святая.
Ей бы можно плакать от обид,
вспомнив все, что вынесла когда-то,
а она о свекле говорит
и спроста краснеет виновато.

Перед наступлением на Ленинград Гитлер заявил: “Ленинград сам поднимет руки: он неминуемо падет, раньше или позже. Никто оттуда не освободится, никто не прорвется через наши линии. Ленинграду суждено умереть голодной смертью”. Но это пророчество Гитлера не сбылось. В Ленинграде продолжали работать хлебозаводы, пекари продолжали печь хлеб.

Из чего же состоял блокадный хлеб?

С начала 1941 г. хлеб выпекался из смеси (200 -граммовый кусок блокадного хлеба):

Пищевая целлюлоза – 20%
Ячменная мука – 4%
Жмых -4%
Отруби – 4%
Овсяная мука – 4%
Соевая мука – 4%
Солодовая мука – 14%
Горох – 15%
Картофель – 15%
Вода – 16%

125-граммовый кусок хлеба:

Пищевая целлюлоза – 10%
Хлопковый жмых – 10%
Обойная пыль – 10%
Вытряски из мешков – 2%
Кукурузная мука – 3%
Ржаная мука – 73%.

Были и другие примеси и добавки, снижавшие питательность хлеба. За все месяцы блокады было выработано при выпечке хлеба около 16 тысяч тонн пищевой целлюлозы. Хлеб с целлюлозой был пышным, а на вкус как полынь.

5. Успехи в кораблестроении.

Интересная задача возникла у моряков в связи с желанием увеличить вероятность попадания в цель при торпедном залпе. Возникла идея за счет искусственного рассеивания увеличить, эту вероятность. Этой задачей занялся один из крупнейших наших математиков академик А.Н. Колмогоров. Ему удалось найти полное решение задачи и довести его до практического использования. Несомненно, что какую-то долю успехов наших моряков следует отнести и на счет этой решенной Колмогоровым задачи. Позднее его выводы были перенесены и на проблемы, связанные со стрельбой зенитной артиллерии по самолетам. Вообще нужно сказать, что актуальная математи­ческая задача, решенная в одной практической ситуации, очень быстро находит и другие применения, порой очень далекие от первоначального направления исследований.

Для примера, крейсер представляет собой такую сложную техническую систему.

Прежде чем начать его постройку, необходимо выявить геометрические обво­ды корпуса судна, чтобы при движении не создавались дополнительные сопротивления и чтобы одновременно он был послушен управляющим воз­действиям руля. Предварительно необходимо обеспечить живучесть корабля, надежность его управления, рассчитать влияние на остойчивость расположения различного рода масс — машин, орудий, торпедных аппаратов и пр. Но и этого мало — требуется обеспечить связь со всеми боевыми единицами корабля, то есть создать эффективную систему управления кораблем и его оружием.

Мы перечислили лишь ничтожную долю тех задач, которые должен ре­шить математик, прежде чем корабль можно начать строить. Но серьезные Задачи необходимо решать и в период его эксплуатации — штурманские расчеты, расчеты стрельб и т.д. Во время второй мировой войны решались проблемы выбора целесообразных действий караванами судов для защиты от нападений подводных лодок, кораблей и самолетов противника. Требовалось указать наилучший вариант поиска подводных лодок или стрельбы зенитной артиллерии.

Стало необходимым сравнивать эффективность различных систем вооружения, результаты различных способов торпедных атак. Первые итоги применения методов

Исследованияопераций американцами и англичанами описаны в книге Ф. М. Морза.

6. Статистический контроль в военном производстве.

В 30-ых гг. стало ясно, что для проведения больших и сложных вычислений, связанных с созданием новых конструкций, абсолютно необходима новая вычислительная техника. Вычислительное бюро, вооруженные арифмометрами» счетами, таблицами, логарифмическими линейками, уже не удовлетворяли потребностей страны. Были необходимые новые принципы организации и производства вычислительных работ. Над этими вопросами серьезно задумались ученые и изобретатели во всем мире, в том числе и в нашей стране! В 30-ых гг. был предложен ряд вычислительных устройств, использующих физические закономерности. Это были моделирующие устройства, позволявшие сравнительно быстро и с хорошей точностью проводить сложные вычисления. Однако каждое из этих устройств было способно решать лишь узкий класс задач, и при этом точность вычислений была ограничена самой конструкцией и точностью физических измерений. Остро назрела необходимость в вычислительных машинах универсального типа, к тому же таких, которые позволяли бы практически неограниченно увеличивать хотеть вычислений в зависимости от потребностей самой проблемы.

Необходимость выпуска огромной массы однородной продукции, с которой неизбежно связано военное производство, привела к постановке задачи исключительной важности: проверке качества больших количеств однородных изделий. При ее решении возникали трудности двоякого характера: во первых, проверка качества каждого изделия, во вторых проверка качества изделий приводит к их непоправимой порче. Нередко проверка качества одного изделия требует несравненно большего времени, чем его изготовление. Так» изготовить винтовочный патрон на соответствующем автомате можно за малую долю минуты, а проверка его качества отнимает много минут; проверка качества взрывателя приводит неминуемой его порче. Как поступать в условиях, когда продукция крайне нужна и ощущается острая нехватка рабочей силы? Выход был найден: использование статистических методов контроля за качеством продукции. Эти методы позволяют при проверке ничтожной доли изготовленных изделий давать достаточно точные заключения о качестве всей партии. При этом удается добиться выигрыша двоякого рода: значительного уменьшения времени на контроль качества изделий и огромного уменьшения порчи изделий при контроле.

7. Разработка ядерного оружия.

Послевоенные годы были омрачены появлением ядерного оружия и исключительно быстрой сменой вооружения во всех странах. Все это требовало значительного внимания к обороне социалистического общества, глубокого осмысливания обстановки.

Необходимо было создавать новые оборонительные системы и разрабатыватъ методы их использования. К математике были предъявлены исключительно высокие требования: появилась необходимость создания новых действенных методов исследования вновь возникавших вопросов. Среди них одними из самых серьезных и первоочередных были вопросы разработки теории оптимального управления, теории операции и статистики случайных полей. В обороне страны стала играть огромную роль вычислительная техника и способы её использования. Возникла необходимость существенно изменить производство испытаний и обработку экспериментальных данных. Огромные скорости самолетов и ракет привели к тому, что на ручной съем экспериментальных данных и на их обработку не остается времени. Всю эту работу необходимо переложить на вычислительные системы. Место математики резко возросло в обороне страны.

Несомненно, что послевоенный период начался в военном деле тремя событиями исключительной важности; появлением ядерного оружия, созданием ядерного оружия, созданием электронных вычислительных машин широким развертыванием работ по ракетной технике. Каждое из указанных направлений конструкторской мысли столкнулись с необходимостью самого широкого привлечения к соответствующим разработкам представителей теоретических областей знания, в первую очередь физиков и математиков. Пришлось создавать огромные научные учреждения, в которых проводилась не только собственно конструкторская работа, но и чисто теоретические исследования - по алгебре, комбинаторному анализу, теории вероятностей.

В математическую теорию полета ракет большой вклад внесли русхкие и советские ученые. Так, еще в 1897 г., профессор Петербургского политехнического института И. В. Мещерский (1859 - 1935) вывел уравнение движения тел переменной массы. Огромный вклад в теорию реактивного движения, как уже отмечалось, внес преподаватель Калужской гимназии К. Э. Циолковский. Выведенные им формулы нашли широкое применение уже в наши дни, в период практического осуществления мечты Циолковского о космических полетах человека. Весьма продуктивными оказались и его идеи многоступенчатых ракет.

Послевоенное развитие ракетостроения привело к необходимости решения вопросов, как инженерного плана, так и управления ракетой во время полета.

Возрастание скоростей самолетов, маневренности танков привело к появлению самонаводящихся ракет. Такие ракеты имеют в своем составе счетно - решающее устройство, которое в зависимости от получаемой информации должно изменять направление движения ракеты. Составление таких программ было связано с решением проблем оптимального управления движением.

Необходимость разработки вопросов оптимального управления разного типами процессами появлялась во многих задачах как оборонного, так и народнохозяйственного характера. Эти проблемы привлекли к себе внимание во всех развитых странах мира. В США методы их решения были предложены Р. Белманом и группой работающих вместе с ним математиков. В нашей стране принципы решения были развиты Л. С. Понтрягиным (1908) и его учениками. Теория Белмана получила наименование динамического программирования Понтрягина - оптимального управления.

8. Создание вычислительной техники.

Первые атомные бомбы, упавшие на города Японии, оживили империалистические силы и дали им в руки козырь, которым они угрожали социалистическим странам. Необходимо было срочно самим создать ядерное оружие. Страна, разоренная в значительной своей части оккупацией и военными действиями, вынуждена была выделить материальные средства и научные силы на быстрейшее преодоление отставания. Физики химики, математики были привлечены к этой работе. Хорошо известно, что напряженный труд увенчался успехами, и отставание в этой области военной техники было преодолено.

Создание первой атомной бомбы требовало не только глубоких теоретических исследований но и хорошо отлаженного технологического процесса по ее изготовлению. На всех стадиях исследований и поисков было необходимо производить сложнейшие вычислительные работы. Обычные приемы вычислений оказывались недостаточными. Появилась крайняя необходимость в их автоматизации и принципиальном убыстрении счета. Эта проблема была включена в программу самых срочных научных изысканий. Первый успех связан с работой группой исследователей Института электротехники Академии Наук Украинской ССР, возглавлявшейся С. А. Лебедевым. В конце 1951 г. они завершили разработку первой в Европе ламповой электронной вычислительной машины, получившей наименование МЭСМ - малая электронная счетная машина. На нее были возложены огромные по своей важности вычислительные работы, в том числе и связанные с задачами обороны страны.

Создание первой машины было успехом кардинального характера, поскольку были разгаданы основные принципы ее действия.

В наше время большое значение имеют малые по размерам легкие и надежные вычислительные! устройства, которые можно помещать непосредственно в ракету, на самолет для автоматического решения разного рода задач. Решение этой технической проблемы связано с появлением новой «элементной базой».

Заметим, что опыт создания и эксплуатации вычислительной техники, накопленный во всем мире, показывает возрастание роли математики и математиков. Теперь уже работа над новыми конструкциями вычислительных машин не мыслится без их участия на всех этапах проектирования, поскольку кому, как не математикам должно быть известно, какие операции используются при решении основных классов вычислительных и логических задач. С другой стороны именно математики составляют программы для производства вычислительных работ. Если в начале организации промышленности вычислительной техники стоимость самой машины забирало львиную долю средств, которые выплачивал покупатель, то в настоящее время стоимость ее математического обеспечения приближается к стоимости самой машины. И это понятно, поскольку без хорошо составленных программ эффективность ее действия будет резко снижена.

В настоящее время имеется много интересных книг по исследованию операций, посвященных преимущественно задачам военного дела. В первую очередь следует указать работу Е. С. Вентцель «Введение в исследование операций» и книгу группы авторов под ред. Ю. В. Чуева «Основы исследования операций в военной технике». Книги значительно отличаются по содержанию, но достаточно полно характеризуют те военные проблемы, к анализу которых применяются методы исследования операций: моделирование боевых действий, сравнение эффективности различных типов вооружения, проблемы наведения летательных аппаратов на цель.

Заключение

Дни Великой Отечественной войны стали достоянием истории. Общий ущерб, нанесенный хозяйству СССР второй мировой войной, составляет 2569 млрд. руб.

Сколько школ можно было бы построить на средства, потерянные нами в годы Великой Отечественной войны, если считать (в ценах, действовавших до 1 января 1961 года), что стоимость строительства новой четырехэтажной школы составляла 8 млн. 600 тыс. руб.

Нам нельзя забывать о том, что подвиг народа в Великой Отечественной войне не ограничивается только славными делами фронтовиков, что основы победы ковались и в тылу, где руками и разумом рабочих, инженеров и ученых создавалась и совершенствовалась военная техника. Нельзя нам забывать и того, что по многим параметрам к концу войны наши танки, самолеты, артиллерийские орудия стали совершеннее тех, которые противопоставлял нам враг. Нельзя забывать, что в конце войны мы вынуждены были вплотную заняться созданием собственного атомного оружия, а для этого пришлось объединить интеллектуальные усилия физиков, химиков, технологов, математиков, металлургов.

Ребята! Со времени Победы прошло 65 лет. Из сообщений, прозвучавших на нашей конференции, вы узнали, как много сделали советские математики для восстановления и развития народного хозяйства нашей страны, а также прогресса теоретической математики.

К сожалению, и теперь положение в мире таково, что страны, а вместе с ней и математики, вынуждены уделять внимание разработке проблем обороны. Однако, это не самоцель, а вынужденная необходимость.

Каждый из нас мечтает о том времени, когда человечество забудет о войнах и подготовке к ним.

Наша страна постоянно предлагает заключить действенные пакты о прекращении гонки вооружений и создать надежные гарантии для мирной жизни народов.

Мы все хотим не разрушения того, что создано трудом многих поколений, а всемирного увеличения, культурных и материальных ценностей.

Мы мечтаем о том времени, когда молодежь сможет отдавать все свои силы мирному труду, познанию законов природы и их использованию на благо человечества.