Бадякина Наталья Ивановна учитель математики МБОУ ИООШ № 21

Внеклассное занятие по математике «Хочу знать математику на пять»

Цели: развитие познавательного интереса, расширение математического кругозора;

создание условий для развития памяти, внимания, мышления;

воспитание самостоятельности, трудолюбия.

Слайд 3: Хитрые задачи

Cколько земли в яме, шириной 2 метра, длиной 2 метра и глубиной 2 метра? (Нисколько: дыры всегда пустые)

Слайд 4 Прочное яйцо. Как бросить яйцо на 5 метров, чтобы оно не разбилось? (Надо кинуть его больше, чем на 5 метров)

Слайд 5 Невероятный прыжок. Как спрыгнуть с десятиметровой лестницы и не разбиться? (Спрыгнуть можно с нижней ступеньки или лестница лежала на земле)

Слайд 6 Викторина «Самый умный, сообразительный»

1.Какое измерение не является единицей длины.

А.Сажень Б.Аршин В.Фунт Б. Фут.

2. Какой из четырёхугольников не является параллелограммом?

А. Квадрат Б. Трапеция В. Ромб Г. Прямоугольник.

3. Кому из математиков принадлежат слова: « математика – царица всех наук»? (немецкий математик Карл Гаусс)

Слайд 7 Графический диктант

• Начертите равнобедренную трапецию.

• Проведите ось симметрии.

• Опустите две высоты. В образовавшихся четырёхугольниках проведите диагонали.

• Через точки пересечения диагоналей проведите прямую.

• Дополните чертёж двумя отрезками так, чтобы образовался орнамент.

• Сколько получилось равных по площади треугольников?

Слайд 8 Загадки

По бумаге я брожу,

Круги и дуги вывожу. (Циркуль)

Не овал я и не круг,
Треугольнику я друг,
Прямоугольнику я брат,
Ведь зовут меня... (квадрат)

Проживают в трудной книжке

Хитроумные братишки.

Десять их, но братья эти

Сосчитают всё на свете (Цифры)

Слайд 9 ЛОГИКА – наука о законах и формах мышления

1. Найдите по 5 сходств и различий между словами радуга и машина.

2.Олег, Игорь и Катя учатся в одном классе. Среди них есть лучший математик, лучший спринтер, лучший художник. Определите кто из них кто: лучший художник не нарисовал своего портрета , но нарисовал портрет Игоря ; Катя никогда не уступала мальчикам в спринте.

(Катя – лучший спринтер, Олег – лучший художник, Игорь – лучший математик)

3. Имеются 2 блузки и 3 юбки. Сколько костюмов можно составить из этих вещей?

Слайд 10 Карпы в пруду.

В деревню приехал профессор. Его попросили определить количество карпов в местном пруду, при этом не вылавливая рыб. Помогите профессору решить проблему. Предложите свой способ.

Надо поймать несколько карпов, пометить их и выпустить. Через некоторое время выловить несколько, и подсчитать в новом улове число помеченных, полагая, что меченые распределились равномерно среди прочих. Таким образом, можно определить численность карпов в пруду.

Слайд 11 Теорема Пифагора

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдём…

Катеты в квадрат возводим,

Сумму степеней находим

И таким простым путём

К результату мы придём

Слайд 12 Интересная задача

По тропинке вдоль кустов

Шло одиннадцать хвостов.

Сосчитать я также смог,

Что шагало тридцать ног.

Это вместе шли куда-то

Петухи и поросята.

А теперь вопрос таков:

Сколько было петухов?

Мне б хотелось также знать

Сколько было поросят?

Предложите несколько способов решения этой задачи.

Задача решается по действиям, системой двух уравнений и уравнением. Выбрать «лучший» способ.

Сдайд 13 Решение задачи по действием и уравнением

1 способ:

2*11 = 22 - ног

30 – 22 = 8 – осталось ног

8 : 2 = 4 – добавляем ноги поросятам

11 – 4 = 7 – петухов

Проверка: 4 * 4 + 7 * 2 = 30 ног

2 способ:

Х – было поросят, 11 – Х – было петухов;

4 * Х – было ног у поросят, 2 ( 11 – Х) – был ног у петухов;

4 * Х + 2* (11 - Х ) = 30 - всего ног

4 * Х – 2 * Х = 30 – 22

2 * Х = 8

Х = 4

4 – было поросят

11 – 4 = 7 – петухов Проверка: 4 * 4 + 7 * 2 = 30 ног

Слайд 14 Решение задачи системой 3 способ:

Х – было поросят, У – было петухов;

4 Х – было ног у поросят, 2 У – был ног у петухов;

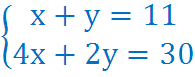
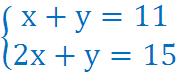
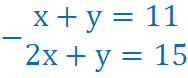
- х = - 4

х = 4 – было поросят; 11 – 4 = 7 – было петухов

слайд 15 Очень трудная задача

Позавчера мне было 10 лет, а на следующий год будет 13. Как такое может быть?

Ответ: Разговор шёл 1 января, а день рождения 31 декабря. 30 декабря было 10 лет, 31 декабря исполнилось 11 лет, в этом году будет 12 лет, а на следующий год будет 13. Всё честно!

Слайд 16 В мире интересного

Многим знакома такая удивительная штука как лента Мёбиуса. Чтобы получить ее, достаточно взять небольшую полоску бумаги, склеить ее, повернув один конец на пол-оборота. Получилась загадочная поверхность, посланная из четырехмерного пространства. Самое удивительное в том, что она односторонняя и ее нельзя перекрасить двумя красками. Такую одностороннюю поверхность впервые рассмотрел в 1858 году немецкий математик Август Фердинанд Мёбиус, ученик «короля математиков» К. Гаусса. Ныне эта поверхность называется листом Мёбиуса. Таинственный и знаменитый лист Мёбиуса имеет удивительные свойства: он имеет один край; одну поверхность. Изучением таких свойств занимается наука топология.

Слайд 17. Удивительные свойства листа Мёбиуса.

ОПЫТ 1. Берём бумажную ленту, разделенную по ширине пополам пунктирной линией. Перекручиваем ленту один раз и концы склеиваем.

Получился знаменитый удивительный лист Мёбиуса. Режем ножницами склеенную ленту посередине, вдоль пунктирной линии. Как вы думаете, что получится? Конечно, если бы мы не перекрутили ленту перед склейкой, все было бы просто: из одного широкого кольца получилось бы два. А что сейчас? Получилось не два кольца, а одно, вдвое уже, но зато вдвое длиннее.

ОПЫТ 2. Приготовьте листы Мёбиуса и повторите опыт 1.

Получили кольцо, перекрученное дважды. А затем разрежем это кольцо еще по середине. Получили два сцепленных друг с другом кольца, каждое из которых дважды перекручено. Вот такие неожиданные вещи происходят с простой бумажной полоской, если склеить из нее лист Мёбиуса.

Слайд 18. Практическое применение

Это свойство ленты запатентовано и нашло практическое применение – абразивный ремень для заточки, ременная передача, красящая лента для печатающих устройств, полоска ленточного конвейера, что помогает работать дольше благодаря тому, что поверхность такой ленты изнашивается равномерно. Еще такие ленты применяют в системах записи на непрерывную пленку с целью увеличения времени записи, в матричных принтерах для увеличения срока годности и многих других местах

Слайд 17 Спасибо за внимание. Всем успехов и удачи!