Тема урока: «Признаки делимости на 3, на 9».

Тип урока: рефлексия.

Основные цели:

– повторение и закрепление учебного материала;

– формирование способность к рефлексии деятельности: фиксированию собственных затруднений по теме «Признаки делимости на 3, на 9», выявлению их причин и построению проекта выхода из затруднений.

1. Самоопределение к деятельности.

– С какими алгоритмами мы познакомились на прошлых уроках? (С алгоритмами определения делимости чисел на 3, на 9).

– С какой целью мы изучили эти признаки? (Для быстрого определения делится то или иное число на данные числа или нет).

– Сегодня у нас урок анализа собственной деятельности. Я думаю, что вы удачно будете использовать, выведенные признаки в своей работе. А если у вас есть затруднения, то к концу урока вы постараетесь их устранить.

– Для успешной работы на уроке повторим признаки, которые мы сегодня будем использовать.

2. Актуализация знаний.

2.1. Все обучающиеся работают вместе, проговаривая алгоритм определения делимости чисел на 3, на 9.

1) Какие из чисел 15; 36; 108; 591; 253; 417; 648; 639; 346:

А) кратны 3; б) кратны 9; в) кратны и 3 и 9.

(Кратные 3:15; 36; 108; 591; 417; 648; 639, т.к. число делится на 3, тогда и только тогда, когда сумма цифр числа делится на 3). На доску вывешивается признак делимости на 3.

Число а делится на 3

Сумма цифр числа а делится на 3

П1

(Кратные 9:36; 108; 648; 639, т.к. числа делятся на 9, тогда и только тогда, когда сумма цифр числа делится на 9).

На доске:

Число а делится на 9

(Кратные 3 и 9:36; 108; 648; 639. Т.к. числа делятся на 3 и на 9 тогда и только тогда, когда сумма цифр числа делится на 9)

На доске:

Число а делится на 3 и на 9

2) Назовите две пары значений переменных x и y, при которых значение выражения 3x + 4y:

а) делится на 3; б) делится на 9;

Работу проводим фронтально, проговаривая формулировки свойств делимости произведения, суммы и разности. По мере того, как звучат свойства, они вывешиваются на доске:

П

ac или bc (a·b)c

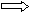4

ac или bc (a±b)c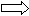

П5

2.1. Самостоятельная работа с самопроверкой по образцу.

– Сейчас вы выполните самостоятельную работу, на неё отводится 10 минут.

1) Какие из чисел 51897; 15639; 62371; 17853; 58986; 75981; 93651; 12736; 87153; 88956.

а) кратны 3; б)кратны 9.

2) Какие цифры можно поставить вместо * в числах 873*; 25*5; 1*43, чтобы полученные числа делились:

А) на 3; б) на 9.

После выполнения работы проходит самопроверка по образцу:

1) а)51897, 15639, 17853, 58986, 75981, 93651, 87153, 88956.

б)58986; 88956;

2) а) 8730; 8733; 8736; 8739.

2505. 2535, 2565, 2595.

1143, 1443, 1743.

Б) 8730, 8739.

2565.

1143.

3. Локализация затруднений.

Учащимся, выполнившим всю работу правильно, предлагаем дополнительное задание: №№ 866,350, 351.

Работаем с учащимися, допустившими ошибки.

– Какие, ошибки могли быть допущены в первом задании? (П1, П2, П3).

– Какие ошибки могли быть допущены при выполнении второго задания? (П1, П2, П3,).

– Какая перед вами стоит задача? (Определить: где допущена ошибка у меня, понять причину, и исправить её).

4. Построение проекта выхода из затруднения.

– Что бы исправить ошибки, что вы должны повторить? (Повторить признаки делимости на 3 и на 9).

– Что вы должны сделать, после того, когда повторите признаки? (Переделать задания и снова сравнить с образцом).

– Если, вы не сможете самостоятельно найти причину ошибки? (Обратится за помощью к учителю, и проверить по эталону).

Учащиеся самостоятельно работают со своей работой.

Те учащиеся, которые выполняют дополнительное задание, по мере его выполнения получают эталоны для проверки своей работы.

Эталоны.

1) а)51897, 15639, 17853, 58986, 75981, 93651, 87153, 88956. – кратны 3, т.к. сумма цифр числа делится на 3: 5+1+8+9+7 = 30, 30 делится на 3, 1+5+6+3+9=24, 24 делится на 3, 1+7+8+5+3=24, 5+8+9+8+6=36, 7+5+9+8+1=30, 9+3+6+5+1=24, 8+7+1+5+3=24, 8+8+9+5+6=36.

б)58986;88956.- кратны 9, т.к. сумма цифр числа делится на 9, тогда 5+8+9+8+6=36 , 36 делится на 9, 8+8+9+5+6=36 , 36 делится на 9.

2) а) 8730. 8733. 8736. 8739 сумма цифр числа делится на 3, т.е. 8+7+3+0=18, 18 делится на 3, 8+7+3+3=21, 8+7+3+6=24, 8+7+3+9=27

2505. 2535, 2565, 2595, сумма цифр числа делится на 3, т.е. 2+5+0+5=12, 2+5+3+5=15, 2+5+6+5=18, 2+5+9+5=21.

1143, 1443, 1743. сумма цифр числа делится на 3, т.е. 1+1+4+3=9, 1+4+4+3=12, 1+7+4+3=15.

Б) 8730, 8739. сумма цифр числа делится на 9, т.е. 8+7+3+0=18, 18 делится на 9. 8+7+3+9=27. 27 делится на 9.

2565. сумма цифр числа делится на 9, т.е. 2+5+6+5=18

1143. сумма цифр числа делится на 9, т.е. 1+1+4+3=9

№ 866.

а) 7005; 7125; 7635.

Б) 5052; 5514; 5466; 5028;…….

№ 350

А) 846, б) 7542, в) 1773, г) 9261, д) 5922, е) 7938.

№ 351.

А) 5373, 5370, 5376, 5379, б) 1125, 1425, 1725, в) 2079, 2379, 2679, 2979, г) 10041, 13041, 16041, 19041, д) 7110, 7140, 7170, е) 5400, 5403, 5406, 5409.

5. Обобщение затруднений во внешней речи.

На данном этапе работает весь класс.

– Какие, ошибки были допущены в работе? (Называются типы ошибок, допущенных в работе).

Проговариваются признаки, на которые были допущены ошибки.

6. Самостоятельная работа с самопроверкой по эталону.

Эту работу выполняют только те учащиеся, которые допустили в первой работе ошибки, они из предложенной работы выбирают только те задания, в которых были допущены ошибки, остальные продолжают выполнять дополнительное задание.

Самостоятельная работа.

1) Какие из чисел 50997; 24639; 60670; 17952; 49986; 75954; 9351; 736; 753; 8856.

а) кратны 3; б)кратны 9.

2) Какие цифры можно поставить вместо * в числах 83*; 5*5; 1*3, чтобы полученные числа делились:

А) на 3; б) на 9.

Эталон.

1) а)50997, 24639, 17952, 49986, 75954, 9351, 753, – кратны 3, т.к. сумма цифр числа делится на 3: 5+0+9+9+7 = 30, 30 делится на 3, 2+4+6+3+9=24, 24 делится на 3, 1+7+9+5+2=24, 4+9+9+8+6=36, 7+5+9+5+4=30, 9+3+5+1=18, 7+5+3=15.

б)49986; 9351.- кратны 9, т.к. сумма цифр числа делится на 9, тогда 4+9+9+8+6=36 , 36 делится на 9, 9+3+5+1=18, 18 делится на 9.

2) а) 831. 834. 837 сумма цифр числа делится на 3, т.е. 8+3+1=12, 12 делится на 3, 8+3+4=15, 8+3+7=18.

525. 555, 585, сумма цифр числа делится на 3, т.е. 5+2+5=12, 5+5+5=15, 5+8+5=18.

123, 153, 183. сумма цифр числа делится на 3, т.е. 1+2+3=6, 1+5+3=9, 1+8+3=12.

Б) 837 сумма цифр числа делится на 9, т.е. 8+3+7=18, 18 делится на 9.

585. сумма цифр числа делится на 9, т.е. 5+8+5=18

153. сумма цифр числа делится на 9, т.е. 1+5+3=9

7. Включение в систему знаний и повторение.

№ 859 один ученик у доски

8. Рефлексия деятельности.

– Какой материал повторяли на уроке?

– Какими правилами пользовались?

– С какими трудностями столкнулись в работе?

– Дайте оценку своей работе на уроке?

– Что необходимо повторить для, успешной работы, на последующих уроках?

9. Домашнее задание: №№865, 860, 862.