Конспект урока по математике "Второй и третий признак подобия треугольников"















 Урок 35. Второй и третий признак подобия треугольников.
Урок 35. Второй и третий признак подобия треугольников.
Цели урока:
Рассмотреть второй и третий признаки подобия треугольников;
Показать применение второго и третьего признаков подобия треугольников при решении задач;
Развивать логическое мышление.
Ход урока
Организационный момент
Сообщить тему урока, сформулировать вместе с классом цели урока.
2. Актуализация знаний учащихся.
Самостоятельно решить задачу №57 с последующим обсуждением решения:
Докажите, что ∆АВF
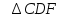 .
.Чему равен коэффициент подобия треугольников ABF и CDF?
Найдите отношение сторон BF и DF.
Чему равно значение DF?
Самостоятельное решение задач на готовых чертежах
В тетрадях записать краткое решение.
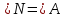 , ВС=12 см, ВМ=6 см, МN= 4 см. Найти: АС.
, ВС=12 см, ВМ=6 см, МN= 4 см. Найти: АС.ВС
 АС, ЕF┴АВ, ВС=12 см, EF= 6 см, АЕ=10 см. Найти: АВ.
АС, ЕF┴АВ, ВС=12 см, EF= 6 см, АЕ=10 см. Найти: АВ.<3=<1+<2, CD= 4 см, ВС= 9 см. Найти: АС. В С
3
2
A C A E C A B
Обсуждение решений задач, с которыми не справились большинство учащихся.
(Пока учащиеся решают задачи, учитель проверяет их решения.)
Решение задач.
∆АВС
 ∆NMВ
∆NMВ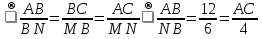 , откуда АС=12∙4:6= 8 Ответ: АС=8 см.
, откуда АС=12∙4:6= 8 Ответ: АС=8 см.∆АВС
 ∆AEF
∆AEF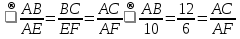 , откуда AB= 10∙12:6=20см Ответ: АВ= 20см.
, откуда AB= 10∙12:6=20см Ответ: АВ= 20см.<3=<1+<2=<САВ
 ∆АСD
∆АСD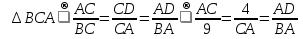 , откуда
, откуда 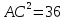 , АС= 6 см (АС
, АС= 6 см (АС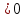 ).
).
Ответ: АС= 6 см.
3. Изучение нового материала
Второй признак подобия треугольников
Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами равны, то такие треугольники подобны.
Учащиеся записывают в тетрадь план-конспект доказательства теоремы.
С1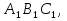
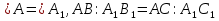 .
.
С ∆
∆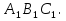
А1
В1 С2 2 1 В А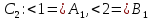 .
.
∆АВ
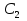 ∆
∆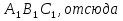
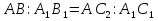 .
.Так как
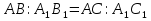 (по условию) и
(по условию) и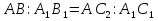 , следовательно АС=А
, следовательно АС=А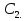
∆АВС=∆АВ
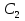 (АВ – общая сторона, АС=А
(АВ – общая сторона, АС=А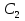 ,
, 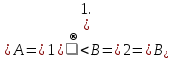
∆АВС
 ∆
∆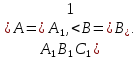
Третий признак подобия треугольников
Теорема: Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
План-конспект доказательства теоремы. (рис. см. выше)
Дано: ∆АВС, ∆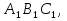
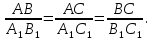
Доказать: ∆АВС ∆
∆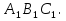
Доказательство:
∆АВ
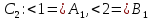
∆АВ
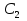 ∆
∆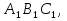 следовательно
следовательно 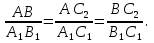
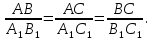 (по условию) и
(по условию) и 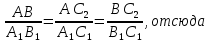 ВС=В
ВС=В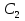 , СА=
, СА=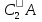 .
.∆АВС=∆АВ
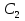 (АВ – общая, ВС=В
(АВ – общая, ВС=В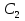 , СА=
, СА=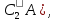 отсюда
отсюда 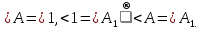 .
.∆АВС
 ∆
∆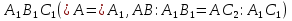
4. Закрепление изученного материала.
Решить № 59, 60 самостоятельно с последующим обсуждением с менее подготовленными учащимися.
Задача №59
-Каким является угол С треугольников АВС и MNC?
-Чему равно отношение сторон, заключающих этот угол (АС:СN и ВС:СМ)?
-Что можно сказать о сторонах АС и ВС треугольника АВС и сторонах CN и СМ треугольника MNC?
-Какой признак подобия треугольников был применён при доказательстве подобия треугольников MNC и АВС?
Задача №60
-Чему равно отношение сторон MN и CD, МР и СЕ, NP и DE треугольников MNP и CDE?
-Что вы можете сказать о сторонах треугольников MNP и CDE?
-Укажите признак, на основании которого треугольники MNP и CDE подобны.
Более подготовленные учащиеся после решения данных задач решают дополнительные задачи.
Дополнительные задачи
В треугольниках АВС и
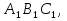 ВЕ и
ВЕ и 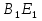 - биссектрисы,
- биссектрисы, 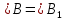 ,
, 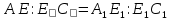 . Докажите, что ∆АВЕ
. Докажите, что ∆АВЕ ∆
∆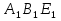 .
.В треугольнике АВС АВ=4, ВС=6, АС=7. Точка Е лежит на стороне АВ. Внутри треугольника взята точка М так, что МВ=5,25, МЕ=4,5, АЕ=1. Прямая ВМ пересекает АС в точке Р. Докажите, что ∆АРВ равнобедренный.
5. Подведение итогов урока
Оценить работу учащихся, подвести итог урока.
Домашнее задание
п.60, 61, вопросы 6,7;
№559,560, 561
Дополнительная задача:
В треугольниках АВС и 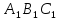 , BD и
, BD и 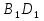 - медианы,
- медианы,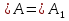 ,
, 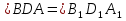 . Докажите, что ∆BDC
. Докажите, что ∆BDC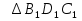 .
.
В работе использованы отредактированные материалы : Гаврилова Н.Ф.
Поурочные разработки по геометрии дифференцированный подход 8 класс.-
2-е изд., перераб. и доп. – М.: ВАКО,2009 .

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ