Открытая олимпиада школьников

«Интеллектуальный марафон» 2012-2013гг.

Математика. 11 класс.

1 часть.

Решения заданий записывать. (За каждое задание 5 баллов, всего 50 баллов).

1. Найдите значение выражения

2. Найдите сумму корней уравнения

3. Найдите наименьшее значение функции на множестве всех действительных чисел.

4. Один из акционеров предприятия имеет 100 акций, номинальная стоимость каждой, из которой составляет 50 рублей. Ежегодно ему выплачивается с каждой акции доход в 50%от ее стоимости. Через сколько лет его общий доход превзойдет удвоенную стоимость акций?

5. Около окружности описана равнобедренная трапеция, у которой средняя линия имеет длину 5 см. Определите периметр трапеции.

6. В равностороннем треугольнике NPO стороной 20 проведена медиана NF. Найдите скалярное произведение векторов и .

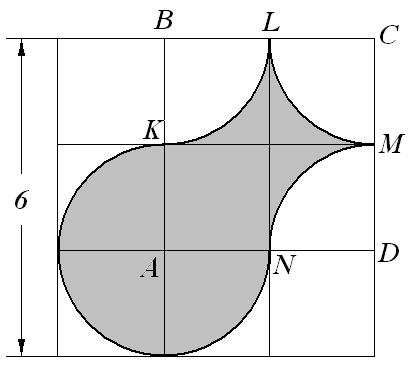
7. Имеется лист фанеры квадратной формы, стороны которого равны 6 дм. Из него, как показано на рисунке, вырезана фигура (KN, KL, LM, MN – дуги с центрами в точках A, B, C, D). Сколько килограммов краски потребуется, чтобы покрасить получившуюся фигуру, если на 1 дм² поверхности расходуется 0,03 кг краски?

8. Найдите все значения а, при которых неравенство х² + (2а + 4)х + 8а + 1 ≤ 0

не имеет решений.

9. Сумма седьмого и двенадцатого членов арифметической прогрессии меньше суммы ее шестого и одиннадцатого членов на 8. Найдите разность прогрессии.

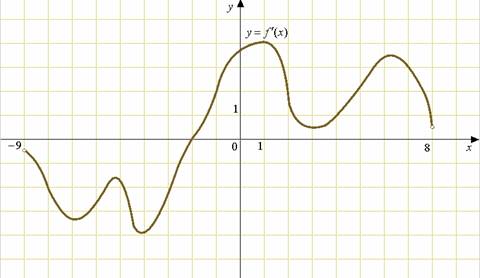
10. На рисунке изображен график производной функции , определенной на интервале(-9;8). В какой точке отрезка[-8;-4]  принимает наименьшее значение.

Часть 2.

1 задание.(10 баллов).

Докажите, что система уравнений 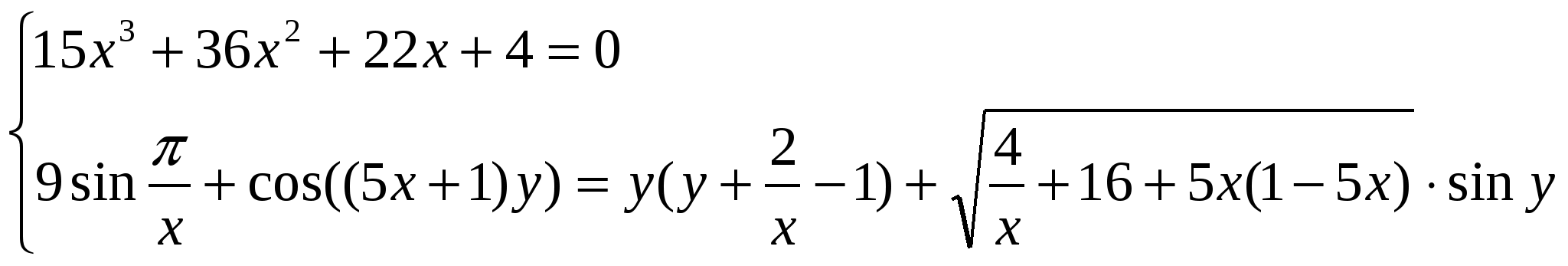не имеет решений.

2 задание.(20 баллов).

Решите уравнение

3 задание.(20 баллов).

Площадь боковой грани правильной треугольной пирамиды равна S₁; а площадь ее сечения, проходящего через боковое ребро и высоту, равна S₂. Найти угол наклона боковой грани к основанию.

Ответы

Часть 1

1

2

3

4

5

6

7

8

9

10

0,25

3,5

5

3

20

300

0,48

1< a < 3

- 4.

-4

Часть 2.

1. Докажите, что система уравнений 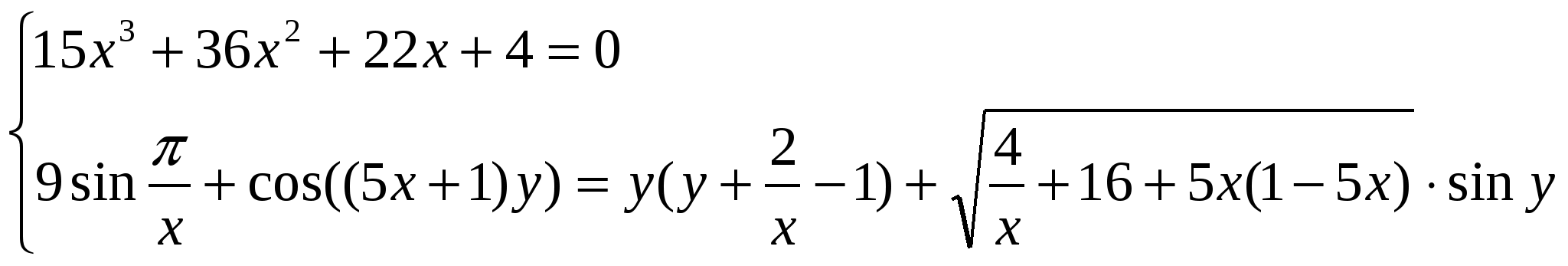не имеет решений.

Решение.

Корень четной степени существует только из неотрицательного числа, значит

, .(3)

Разложим числитель на множители. Для этого решим уравнение . Так как сумма коэффициентов равна нулю: -25+5+16+4=0, то x=1 является корнем.

Воспользуемся схемой Горнера.

-25

5

16

4

1

-25

-20

-4

0

, , ,5x+2=0, x=-0,4.

Неравенство (3) примет вид:,,

ООС

Решим уравнение (1)..Пусть 5x=t, тогда уравнение примет вид: | *25, получим .Замечаем, что ни одно положительное число не может быть корнем, так как все коэффициенты положительны. Если уравнение имеет целые корни, то они являются делителями свободного члена. Воспользуемся схемой Горнера.

3

36

110

100

-2

3

30

50

0

t=-2 является корнем. Решим квадратное уравнение: ,уравнение имеет два действительных корня.. Имеем: или , или . , входит в ООС.

Подставим найденный корень x=-0,4 в уравнение (2), получим:,

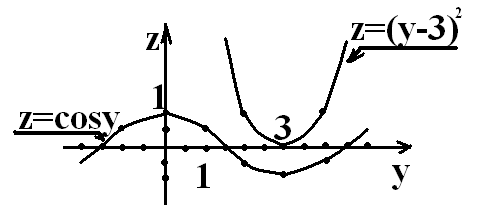
,. В системе координат zOy построим графики функций : и .Графики не пересекаются, значит, уравнение не имеет решений.

Ответ: решений нет.

2. Решите уравнение .

Решение. ОДЗ уравнения .

Используя неравенство Коши имеем: ; ; ; ; .

Сложив последние неравенства получим: Тогда: 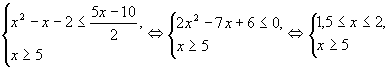Последняя система решений не имеет.

Ответ: корней нет.

3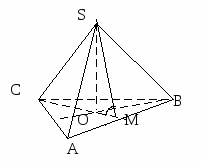
. Площадь боковой грани правильной треугольной пирамиды равна S₁; а площадь ее сечения, проходящего через боковое ребро и высоту, равна S₂. Найти угол наклона боковой грани к основанию.

Решение:

Пусть S_ASB = S₁; S_SCM = S₂.

Обозначим сторону основания пирамиды через а; угол наклона боковой грани к основанию - a.

Имеем: a = ÐSMC, где CM – медиана, биссектриса и высота DABC, опущенная из вершины С. Выразим S₁ и S₂ через неизвестные параметры а и a.

S₁ = .

Рассмотрим DSOM – прямоугольный. OM = CM (т.к. О – точка пересечения медиан DABC, делит СМ в отношении 2:1, считая от вершины С); SM = OM/Cosa; SO = OM×tga.

Рассмотрим DABC; CM –высота, медиана.

.

Тогда ; .

Найдем S₁ = .

Выразим S₂ через а и a. Рассмотрим D CMS; S₂ = S_DCMS = CM×SO.

Имеем систему уравнений:

Выразим а² из первого и второго уравнений и приравняем а². Имеем:

Þ

Так как , (a - линейный угол двугранного угла, ), то

.

Ответ: если .

Критерии оценивания.

Каждая работа оценивается и проверяется не менее чем 2-мя членами жюри.

1 часть (5 баллов за каждое задание).

5 баллов ставится за верное решение;

4 балла – за верное решение с недочетом;

2-3 балла – решение в основных чертах верное, но неполное или содержит непринципиальные ошибки;

1 балл – решение в целом неверное, но содержит более или менее существенное продвижение в верном направлении;

0 баллов – решение неверное или отсутствует.

2 часть.

1 задание.

10 баллов – решение верное, даны необходимые пояснения;

5 баллов – идея решения верная, недостаточны пояснения или допущена техническая ошибка;

0 баллов – решение неверное или отсутствует.

2 задание.

20 баллов – решение верное, правильно выбран метод решения и приведены необходимые пояснения;

15 баллов – решение доведено до конца, сделаны необходимые пояснения, но не указана ОДЗ;

10 баллов – идея решения верная, решение доведено до конца, но не указана ОДЗ, есть техническая ошибка в решении уравнения, влияющая на ответ;

5 баллов – нет необходимых пояснений или допущена ошибка в составлении ОДЗ и решении неравенства, решение не доведено до конца, но содержит более или менее существенное продвижение в верном направлении;

0 баллов – решение неверное или отсутствует совсем.

3 задание.

20 баллов – решение верное и приведены необходимые пояснения;

15 баллов – решение верное, но нет необходимых пояснений;

10 баллов – идея решения верная, решение доведено до конца, но с технической ошибкой;

5 баллов – идея решения верная, но нет необходимых пояснений и решение задачи не доведено до конца;

0 баллов – решение неверное или отсутствует совсем.