Муниципальное общеобразовательное учреждение средняя общеобразовательная школа с углублённым изучением отдельных предметов № 1 г. Малмыжа Кировской области

Районный конкурс «Учитель года – 2009»

МАСТЕР-КЛАСС

«ПРОГНОЗИРОВАНИЕ РЕЗУЛЬТАТА АРИФМЕТИЧЕСКОГО ДЕЙСТВИЯ

НА УРОКЕ МАТЕМАТИКИ»

Брюхачёва Алевтина Анатольевна

учитель начальных классов

Февраль 2009 года

Формирование вычислительных навыков – одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе. Поскольку вычислительные навыки необходимы как в практической жизни человека, так и в учении. Данная тема актуальна, так как математика является одной из важнейших наук на Земле, и именно с ней человек встречается каждый день в своей жизни. Вычислительные навыки как составная часть математической культуры современного человека имеют большое прикладное значение в учебной и в дальнейшей трудовой деятельности, является тем запасом знаний, умений, который находит повсеместное применение.

Умение пользоваться микрокалькулятором стало неотъемлемой частью математической культуры современного человека. Конкретные числа и действия машине задаёт человек. В некоторых ситуациях машина может дать сбой либо задающий ей числа и операции допускает ошибку. Младший же школьник, используя микрокалькулятор, естественно не сомневается в истинности результатов, которые выдаёт машина. Поэтому для предупреждения ошибок в вычислении я считаю, что младших школьников надо учить давать предварительную оценку результатам на основании округления исходных данных и промежуточных результатов действий, то есть выполнять прикидку результатов (числа цифр результатов, его последней цифры с помощью предварительного округления, на основании зависимости между результатами и компонентами арифметических действий). Следовательно, одной из важных характеристик вычислительных навыков является умение прогнозировать результат и оценивать его истинность, которое необходимо в дальнейшем обучении при изучении целого ряда предметов среднего и старшего звена.

В толковом психологическом словаре «прогноз» - в общем смысле: предсказание хода и результата любого процесса. У Я.И.Грудёнова «прогнозирование – это предвидение тех результатов, к которым может привести поиск». В современной психологии считают, что человек ищет и находит решение любой задачи на основе непрерывного прогнозирования искомого, то есть некоторого предвидения, получаемого результата в процессе анализа, синтеза, обобщения. В школе же под прогнозированием понимается предварительное оценивание результатов арифметических действий, позволяющее избежать очевидных ошибок в вычислениях.

Из бесед с учителями математики я выявила, что многие дети, приходя в 5 класс, испытывают трудности в выборе действия при решении задач, допускают ошибки при делении многозначного числа на однозначное и двузначное, особенно когда в частном есть нули. Я пришла к выводу, что действительно приём прогнозирования должен формироваться в начальной школе. Приём прогнозирования является пропедевтикой для изучения математики в среднем и старшем звене, тем более когда школа имеет статус углублённого изучения математики. В начальном курсе математики такие задания особенно актуальны при изучении арифметических действий с многозначными числами, основу которых составляет также усвоение алгоритмов письменного умножения и деления.

Так как у меня четвёртый класс, поэтому использование приёма прогнозирования покажу на примере задания для 4 класса. Но как только становится возможным, по мере изучения тем я ввожу этот приём с первого класса.

На этапе актуализации знаний я использую следующие виды заданий:

1. Выбери число, которое может получиться при умножении двух других:

60, 15, 4

7, 98, 14

9, 144, 16

6, 18, 108

2. Какой цифрой может быть записано частное чисел? Назови верное частное.

420 : 96

302 : 39

3, 4, 5

7, 8, 9

109 : 13

256 : 27

7, 8, 9

7, 8, 9

3. Поставьте нужные знаки действий, чтобы равенства были верными?

4500 * 9 * 800 = 1300

6400 * 8 * 200 = 800

500 * 7 * 500 = 3000

300 * 6 * 200 = 2000

4. Не вычисляя, расположи выражения в порядке возрастания их значений:

а) 3009 х 4; 309 х 6; 4207 х 4; 352 х 6; 319 х 6

б) 2018 х 5; 218 х 7; 4057 х 5; 457 х 7; 208 х 7

5. Не производя вычислений, сравни и поставь знак:

38 х 7 + 38 х 3 … 38 х 11

76 х 5 х 7 … 76 х 12

3806 х (3 + 8) … 3806 х 3 + 3806

5060 х 6 … 5600 х 6

Применение приёма прогнозирования на этапе актуализации знаний помогает увеличить скорость и правильность устных вычислений. Это своего рода математическая разминка, гимнастика ума перед дальнейшей работой по теме.

На этапе изучения нового при делении и умножении многозначного числа на однозначное предлагаю задания следующего типа:

1. Подчеркни первое неполное делимое и определи количество цифр в частном:

3294 6 5392 4 254105 5 8320 8

2. Выполняя деление в следующих случаях:

9870 : 35

136576 : 64

95345 : 485

76171 : 19

720036 : 36

ученик в частном получил: 1) трёхзначное число; 2) четырёхзначное число; 3) двухзначное число; 4) четырёхзначное число; 5) трёхзначное число.

В каких случаях частное найдено неверно?

3. Не выполняя действия деления, укажи, какие из равенств неверны:

116174 : 58 = 20344

172 : 9 = 4908

21476 : 7 = 368

4. Найди ошибки, не производя вычислений, способом прикидки:

8004 х 9 = 7236

978 х 8 = 73484

4567 х 8 = 325536

8352 х 7 = 58464

5. Не вычисляя, определите, сколько цифр будет в записи значений выражений:

2395 х 3

2395 х 6

12395 х 5

22395 х 5

В ходе изучения нового использование приёма прогнозирования способствует более прочному усвоению нового материала, помогает предупредить ошибки в вычислениях.

На этапе закрепления нового предлагаю задания следующего вида:

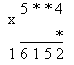
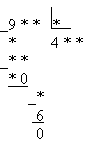
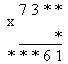
Это задание повышенной трудности, рассчитанное на более высокий уровень интеллекта.

Умение решать задачи включает в себя овладение конкретными способами решения. Кроме того, большое значение имеет умение догадываться, подбирать ответ задачи. При решении задач геометрического характера предлагаю задания следующего содержания:

1. Периметр прямоугольника – 44см, его площадь – 72 см². Какими могут быть длины сторон этого прямоугольника?

Длина

Ширина

9 см

24 см

20 см

21 см

18 см

8 см

3 см

2 см

1 см

4 см

2. Догадайся, какой единицей длины пользовались при измерении?

Длина кисточки – 19___

Ширина моста – 11___

Длина скрепки – 19___

Расстояние между городами – 19___

Площадь кухни – 8___

При составлении и подборе текстовых задач особое внимание уделяю содержанию задачи: включаю ситуации, с которыми ребёнок сталкивается в повседневной жизни.

Текстовые задачи:

• Разность двух чисел 70. Одно число больше другого в 11 раз. Найдите эти числа.

• У Кати было 324 рубля. Сможет ли она купить 6 килограммов апельсинов по цене 54 рубля за килограмм?

• Можно ли 25 человек рассадить в два ряда поровну?

• У отца 3000 рублей. Стоимость одного билета в аквапарк 600 рублей. Сможет ли он сводить четверых своих детей?

• В столовую ложку вмещается 25 граммов муки, а в стакан – 130 граммов муки. Сколько примерно столовых ложек муки вмещается в стакан?

Таким образом, формирование умения прогнозировать, предвидеть результаты является важным компонентом развития логического мышления учащихся. Данное умение важно не только как одно из качеств осознанного вычислительного навыка, но и необходимо при решении любой задачи и в дальнейшей трудовой деятельности.

Уважаемые коллеги, ваше внимание обращаю на задание следующего содержания и предлагаю выполнить.

Прикиньте, можно ли указанный в таблице товар унести в сумке, выдерживающей не более двух килограммов?

Книги

Масса, г

Количество

Словарь

Учебник

Справочник

Стихи

240

350

120

50

2

3

1

5

• Как можно облегчить усвоение материала, используя метод прогнозирования на ваших предметах?

• А в каких жизненных ситуациях вы применяете умение прогнозировать результат?

• А сейчас у меня вопрос к учителям математики. Как вы думаете, необходимо ли учить этому с начальной школы? Каким образом это облегчает процесс обучения в среднем звене?

Выполнение подобных заданий на прогнозирование результата в процессе формирования вычислительных навыков позволит сформировать у школьников умение оперировать учебным материалом: умение анализировать, сравнивать, выдвигать предположения, подтверждать или опровергать их, активно использовать ранее усвоенные знания, что будет способствовать становлению высокой математической культуры современного человека. Приём прогнозирования развивает саморефлексию учащихся и готовит к решению задач в жизненных ситуациях.