Урок №3.

Тема: Отрезок. Длина отрезка.

Оборудование: линейка с делениями.

Новый материал: Отрезок. Длина отрезка.

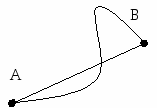?: Как можно соединить 2 точки?

• С помощью кривой линии.

• С помощью прямой линии.

?: Как легко провести прямую линию. – С помощью линейки.

Обозначим точки буквами A и B. Тогда мы получим отрезок AB. Но этот же отрезок можно обозначить и BA.

AB – отрезок.

A, B – концы отрезка.

Л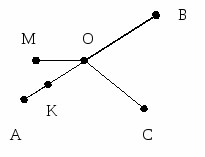юбые 2 точки можно соединить только одним отрезком.

Поставим ещё несколько точек: C, K, O, M.

?: Какие точки принадлежат отрезку AB? – A, B, K, O.

?: Какие точки не принадлежат отрезку AB? – M, C.

Отрезки можно ещё сравнивать. Посмотрите внимательно на отрезки AO и OB.

?: Что можно про них сказать? – Они равны.

Это записывают так: AO=OB.

?: А вот что можно сказать об отрезках AB и AK? - Отрезок AK короче, или меньше, чем отрезок AB. Или: отрезок AB длиннее, или больше, чем отрезок AK.

А всё потому, что отрезок AK – это часть отрезка AB. А часть всегда больше, чем целое.

?: А как сравнить отрезки AB и КС, если отрезок KC не является частью AB? Как можно ещё сравнивать отрезки? – Можно измерить их линейкой.

Т.е. можно измерить их длины.

Практическая работа:

1. рис.4 в учебнике. Измерить длину отрезка AB.

1. С помощью линейки;

2. С помощью единичного отрезка.

Длина отрезка AB равна – 5см. Записывают так: AB=5 см.

?

10 см. = 1 дм.

100 см. = 1 м.

1 см. = 10 мм.

1 км. = 1000 м.

: А какие ещё единицы измерения длины вы знаете? – дециметр, метр, миллиметр, километр.

Давайте вспомним, как одни единицы длины выражаются через другие:

2. Учебник: №44, 45.

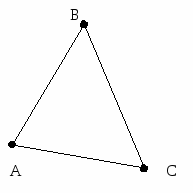
Возьмем теперь три точки. Соединим их попарно отрезками. Получим фигуру – треугольник. Треугольник состоит из вершин сторон. Вершины – это точки, а стороны – отрезки.

ABC – треугольник.

A, B, C – вершины треугольника.

A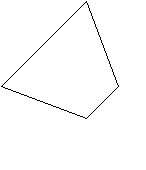B, BC, AC – стороны треугольника.

А теперь добавим ещё точку: получилось уже 4 точки, мы снова соединим их отрезками следующим образом. Тогда мы получим четырёхугольник.

?: Где у него будут вершины? Стороны?

?: Можно ли изобразить 5-угольник? 6-угольник?

Изобразите в тетради 4-угольник, 5-угольник, 6-угольник.

Назовите стороны получившихся фигур.

Треугольники, 4-угольники, 5-угольники и т.д. можно назвать одним словом – многоугольники.

Задачи:

1. Учебник: №30 – письменно.

2. Учебник: №32 –устно.

3. Учебник: №33 – письменно.

4. Учебник: №38 (б,в,г) – письменно.

5. Учебник: №41 – письменно.

Домашнее задание: устно - §2(прочитать, выучить определения), письменно - №64, 65, 67.