Урок №6-7.

Тема: Шкалы и координаты: меньше и больше.

Оборудование: линейка, модель координатного луча.

Повторение:

1. Игра: Математическое ЛОТО.

Правила: На карточке на поле 3х3 в каждой клетке – числа. Это ответы на некоторые вопросы учителя. Учитель читает задания. Ученик решает его и в карточке зачеркивает тот ответ, который у него получился. Всего 5 вопросов, значит, незачеркнутыми должны остаться 4 числа.

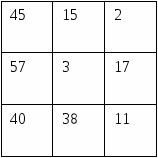
Вопросы:

1. Из точки с координатой 48 сдвинулись влево на 3 единицы. Какова координата получившейся точки? (45)

2. Из точки с координатой 20 сдвинулись в точку с координатой 37. На сколько единиц передвинулись? (17)

3. Из некоторой точки перешли влево на 7 единиц в точку с координатой 31. Из точки с какой координатой передвинулись? (38)

4. Из точки с координатой 29 передвинулись вправо на 28 единиц. Какова координата получившейся точки? (57)

5. Из точки с координатой 75 перешли в тотчку с координатой 64. На сколько единиц мы передвинулись? (11)

Новый материал:

Посмотрим снова на координатный луч, а точнее, на координаты точек. Что мы заметим?

• Как изменяются числа по мере того, как мы двигаемся вправо? (Чем дальше вправо, тем больше координата точки)

  • Точка с меньшей координатой лежит левее точки с большей коодинатой.

  • Точка с большей коодинатой лежит правее точки с меньшей коодинатой.

Упражение 1: Указать расположение двух точек

ПРИМЕР: Точка А(15) лежит левее точки В(23), потому что координата точки А меньше, чем координата точки В.

1. А(15) и В(23);

2. С(43) и D(18);

3. М(36) и Р(33).

4. А(11) и О(0).

Мы только что сравнивали расположение точек на координатном луче, для этого мы сравнивали координаты этих точек.

Давайте теперь выполним следующее упражнение:

Упражнение 2: Сравнить координаты двух точек точек и записать:

ПРИМЕР: 2 < 8 - координата точки В меньше, чем координата точки К.

1. В(2) и К(8);

2. А(3 и М(6);

3. S(11) и М(6);

4. К(8) и S(11);

5. А(3) и О(0).

• Как называется запись: 2 < 8 ? (неравенство)

• Вспомним, как называются знаки:

< - меньше;

> - больше.

• Можно ли записать так: В(2)<К(8)? (нельзя, потому что сравниваем мы числа, а не точки. Нельзя сравнить точки с помощью знаков > или <).

Упражение 3: Сравнить координаты точек, зная только расположение точек на координатном луче:

ПРИМЕР: Координата точки А меньше, чем координата точки М, потому что точка А находится левее точки М.

1. А и М;

2. В и М;

3. N и Р;

4. В и Р;

5. С и А;

6. D и О;

7. D и А.

Упражение 4: Сравнить координаты точки с координатами двух точек:

ПРИМЕР: Координата точки В меньше координаты точки М, но больше координаты точки Е, поэтому пишем 1<2<6.

• Запись 1<2<6 – называется двойным неравенством.

• Читается: 2 больше 1, но меньше 6.

1. В(2) и М(6), Е(1).

2. К(8 и А(3), S(11).

3. М(6) и O(0), Р(13).

Мы с вами сравнивали координаты точек, а теперь будем сравнивать отрезки.

• Что нужно знать, чтобы сравнивать отрезки? (их длины. Тот отрезок болше, длина которого больше)

Отрезки будем тоже сравнивать с помощью знаков < или >.

Упражнение 5: Поставить верный знак:

ПРИМЕР: Отрезок АВ меньше отрезка CD, потому что длина отрезка АВ меньше длины отрезка CD.

1. АВ=41 см. СD=53 cм.

2. КА=7 см. ВМ=1 см.

3. СК=81 см. CD=8 дм. 1 см.

4. СМ=35 см. РА=3 дм 3 см.

5. SC=9 м. SM=905 см.

Упражение 6: Сравнить отрезки с помощью двойного неравенства:

ПРИМЕР: Отрезок АВ больше отрезка СК, но меньше отрезка CD, потому что 2<3<5.

1. АВ=3 см. CD=5 см. СК=2 см.

2. СК=35 см. КМ=15 см. МТ=10 см.

3. РМ=1 дм.1 см. РК=1 дм.7 см. РО=2 дм.

• Как быть, если числа очень большие? Например: как сравнить числа 712 и 1037?

  1. 712 и 1037. Какое число больше? Почему?

     • Из двух чисел с разным количеством знаков больше то, у которого знаков больше.

2. А если в числах равное количество знаков? Как быть тогда?

   • Тогда начинаем сравнивать по разрядам. Начинаем с самого старшего.

ПРИМЕР 1: Начинаем со старшего разряда: 2<3, значит 2170<3004.

ПРИМЕР 2: Начинаем со старшего разряда 2=2, поэтому сраниваем меньшие разряды: 8<9, значит 2870 меньше, чем 2905.

1. 2170 и 3004;

2. 2870 и 2905

3. 10093 и 10193.

4. 2487 и 2475.

5. 1109 и 1106.

Задания на урок:

1. №142, 143.

2. №145.

3. №147, 149.

4. №148 (№150).

5. №151, 155.

6. Какое из чисел больше и на сколько?

   1. 144 или 128?

   2. 350 или 500?

   3. 123 или 215?

7. Какое из чисел меньше и на сколько?

   1. 275 или 300?

   2. 195 или 224?

8. Какое из чисел больше и во сколько раз?

   1. 100 или 1000?

   2. 45 или 15?

   3. 120 или 40?

9. Назовите 2 ближайших числа, между которыми находятся числа:

   1. 28

   2. 84

   3. 219

   4. 145.

Домашнее задание:

1. стр. 35-36 – прочитать.

2. №165, 167, 168(г,д), 171(а,в).